Moltiplicazione di un numero per una matrice

In questa pagina vedremo come moltiplicare un numero per una matrice. Hai anche esempi che ti aiuteranno a capirlo perfettamente ed esercizi risolti in modo che tu possa esercitarti. Troverai anche tutte le proprietà del prodotto di uno scalare e di una matrice.

Come moltiplicare un numero per una matrice?

Per moltiplicare un numero per una matrice , moltiplica ogni elemento della matrice per il numero.

Esempio:

Risolti i problemi di moltiplicazione di un numero per una matrice

Esercizio 1:

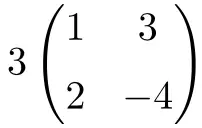
Esercizio risolto del prodotto di un numero per una matrice 2x2, operazioni con le matrici

vedi soluzione

È una moltiplicazione di uno scalare per una matrice quadrata di ordine 2:

$\displaystyle 3 \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & -4 \end{pmatrix} = \begin{pmatrix} 3\cdot 1 & 3\cdot 3 \\[1.1ex] 3\cdot 2 & 3\cdot (-4) \end{pmatrix} = \begin{pmatrix} \bm{3} & \bm{9} \\[1.1ex] \bm{6} & \bm{-12} \end{pmatrix}$

Esercizio 2:

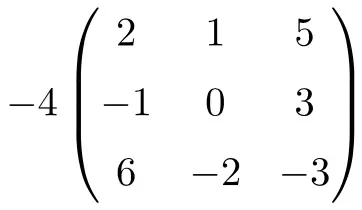
esercizio risolto passo passo di moltiplicazione di un numero per una matrice 3x3, operazioni con matrici

vedi soluzione

È un prodotto di un numero per una matrice quadrata di ordine 3:

$\displaystyle -4 \begin{pmatrix} 2 & 1 & 5 \\[1.1ex] -1 & 0 & 3 \\[1.1ex] 6 & -2 & -3 \end{pmatrix} = \begin{pmatrix} -4 \cdot 2 & -4 \cdot 1 & -4 \cdot 5 \\[1.1ex] -4 \cdot (-1) & -4 \cdot 0 & -4 \cdot 3 \\[1.1ex] -4 \cdot 6 & -4 \cdot (-2) & -4 \cdot (-3) \end{pmatrix}= \begin{pmatrix} \bm{-8} & \bm{-4} & \bm{-20} \\[1.1ex] \bm{4} & \bm{0} & \bm {-12} \\[1.1ex] \bm{-24} & \bm{8} & \bm {12} \end{pmatrix}$

Esercizio 3:

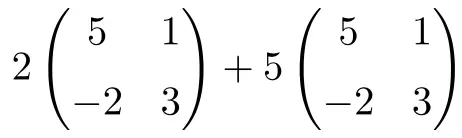
Esercizio risolto di moltiplicazione di un numero per una matrice 2x2, operazioni combinate con le matrici

vedi soluzione

È un’operazione che combina prodotti di numeri per matrici e somme di matrici di dimensione 2×2:

$\displaystyle 2 \begin{pmatrix} 5 & 1 \\[1.1ex] -2 & 3 \end{pmatrix}+5\begin{pmatrix} 5 & 1 \\[1.1ex] -2 & 3 \end{pmatrix}$

Pertanto, dobbiamo prima risolvere i prodotti:

$\displaystyle \begin{pmatrix} 10 & 2 \\[1.1ex] -4 & 6 \end{pmatrix}+\begin{pmatrix} 25 & 5 \\[1.1ex] -10 & 15 \end{pmatrix}$

E infine aggiungiamo le matrici risultanti:

$\displaystyle \begin{pmatrix} \bm{35} & \bm{7} \\[1.1ex] \bm{-14} & \bm{21} \end{pmatrix}$

Esercizio 4:

Consideriamo le seguenti matrici:

$\displaystyle A=\begin{pmatrix} 2 & -3 & 5 \\ 1 & 4 & 0 \\ -3 & 2 & -5 \end{pmatrix} \qquad B=\begin{pmatrix} 6 & 0 & 2 \\ -3 & 4 & 1 \\ 3 & 2 & 7 \end{pmatrix}$

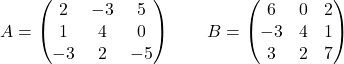
Calcolare:

$\displaystyle -2A+5I-3B$

vedi soluzione

È un’operazione che combina moltiplicazioni scalari con addizioni e sottrazioni di matrici di dimensione 3×3. Inoltre, la matrice

$I$

è la matrice identità, che è composta da 1 sulla diagonale principale e 0 sul resto degli elementi:

$\displaystyle -2\begin{pmatrix} 2 & -3 & 5 \\[1.1ex] 1 & 4 & 0 \\[1.1ex] -3 & 2 & -5 \end{pmatrix}+5\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} -3 \begin{pmatrix} 6 & 0 & 2 \\[1.1ex] -3 & 4 & 1 \\[1.1ex] 3 & 2 & 7 \end{pmatrix}$

Pertanto, eseguiamo prima le moltiplicazioni:

$\displaystyle \begin{pmatrix} -4 & 6 & -10 \\[1.1ex] -2 & -8 & 0 \\[1.1ex] 6 & -4 & 10 \end{pmatrix}+\begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 0 & 5 & 0 \\[1.1ex] 0 & 0 & 5 \end{pmatrix} - \begin{pmatrix} 18 & 0 & 6 \\[1.1ex] -9 & 12 & 3 \\[1.1ex] 9 & 6 & 21 \end{pmatrix}$

Aggiungiamo le prime due matrici:

$\displaystyle \begin{pmatrix} 1 & 6 & -10 \\[1.1ex] -2 & -3 & 0 \\[1.1ex] 6 & -4 & 15 \end{pmatrix}-\begin{pmatrix} 18 & 0 & 6 \\[1.1ex] -9 & 12 & 3 \\[1.1ex] 9 & 6 & 21 \end{pmatrix}$

Infine, eseguiamo la sottrazione delle matrici:

$\displaystyle \begin{pmatrix} \bm{-17} & \bm{6} & \bm{-16} \\[1.1ex] \bm{7} & \bm{-15} & \bm{-3} \\[1.1ex] \bm{-3} & \bm{-10} & \bm{-6} \end{pmatrix}$

Se questi esercizi sui prodotti scalari di matrici ti sono stati utili, non esitare a esercitarti con gli esercizi risolti passo passo sulla somma di matrici e sul prodotto di matrici , i due tipi di operazioni su matrici che si ripetono su più.

Proprietà del prodotto di un numero per una matrice

Come ben sai, esistono molti tipi di matrici : matrici quadrate, matrici triangolari, matrice identità, ecc. Ma, fortunatamente, tutte le proprietà del prodotto di numeri per matrici valgono per tutte le classi di matrici.

Ecco le proprietà della moltiplicazione tra scalari e matrici:

Proprietà associativa:

$a \cdot (b \cdot A) = (a \cdot b) \cdot A$

Osserva le due operazioni seguenti perché danno lo stesso risultato indipendentemente da come moltiplichiamo 2 e 3:

$\displaystyle 2 \cdot \left(3 \cdot \begin{pmatrix} 1 & 0 \\[1.1ex] 2 & -1 \end{pmatrix} \right) =2 \cdot \begin{pmatrix} 3 & 0 \\[1.1ex] 6 & -3 \end{pmatrix} = \begin{pmatrix} \bm{6} & \bm{0} \\[1.1ex] \bm{12} & \bm{-6} \end{pmatrix}$

$\displaystyle (2 \cdot 3) \cdot \begin{pmatrix} 1 & 0 \\[1.1ex] 2 & -1 \end{pmatrix} =6 \cdot \begin{pmatrix} 1 & 0 \\[1.1ex] 2 & -1 \end{pmatrix} = \begin{pmatrix} \bm{6} & \bm{0} \\[1.1ex] \bm{12} & \bm{-6} \end{pmatrix}$

Proprietà distributiva rispetto all’addizione di scalari:

$(a+b) \cdot A = a \cdot A+ b \cdot A$

Come puoi vedere nell’esempio qui sotto, è lo stesso se prima aggiungiamo 1+2 e poi lo moltiplichiamo per una matrice, oppure se moltiplichiamo la matrice separatamente per 1 e per 2 e poi aggiungiamo i risultati:

$\displaystyle (1 + 2) \cdot \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5 \\[1.1ex] -2 & -4 \end{pmatrix} =3 \cdot \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5 \\[1.1ex] -2 & -4 \end{pmatrix}= \begin{pmatrix} \bm{6} & \bm{-3} \\[1.1ex] \bm{9} & \bm{15} \\[1.1ex] \bm{-6} & \bm{-12} \end{pmatrix}$

$\displaystyle 1 \cdot \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5 \\[1.1ex] -2 & -4 \end{pmatrix} + 2 \cdot \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5 \\[1.1ex] -2 & -4\end{pmatrix} = \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5\\[1.1ex] -2 & -4 \end{pmatrix} + \begin{pmatrix} 4 & -2 \\[1.1ex] 6 & 10 \\[1.1ex] -4 & -8\end{pmatrix}= \begin{pmatrix} \bm{6} & \bm{-3} \\[1.1ex] \bm{9} & \bm{15} \\[1.1ex] \bm{-6} & \bm{-12} \end{pmatrix}$

Proprietà distributiva rispetto all’addizione di matrici:

$a \cdot \left(A + B \right) = a \cdot A + a \cdot B$

In altre parole, sommare due matrici matematiche e poi moltiplicarle per un numero equivale a moltiplicare separatamente le due matrici per lo stesso numero e poi sommare i risultati. Nell’esempio seguente puoi verificare:

$\displaystyle 4 \cdot \left( \begin{pmatrix} 3 & -2 \\[1.1ex] 6 & -1 \end{pmatrix}+\begin{pmatrix} -1 & 3 \\[1.1ex] 0 & 4 \end{pmatrix} \right) =4 \cdot \begin{pmatrix} 2 & 1 \\[1.1ex] 6 & 3 \end{pmatrix}= \begin{pmatrix} \bm{8} & \bm{4} \\[1.1ex] \bm{24} & \bm{12} \end{pmatrix}$

$\displaystyle 4 \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 6 & -1 \end{pmatrix}+ 4 \cdot \begin{pmatrix} -1 & 3 \\[1.1ex] 0 & 4 \end{pmatrix} = \begin{pmatrix} 12 & -8 \\[1.1ex] 24 & -4 \end{pmatrix}+\begin{pmatrix} -4 & 12 \\[1.1ex] 0 & 16 \end{pmatrix} = \begin{pmatrix} \bm{8} & \bm{4} \\[1.1ex] \bm{24} & \bm{12} \end{pmatrix}$

Proprietà dell’elemento neutro:

$1 \cdot A = A$

Pertanto, quando moltiplichiamo una matrice per 1, non modifichiamo la matrice:

$\displaystyle 1 \cdot \begin{pmatrix} 5 & -4 & 0 \\[1.1ex] 1 & 3 & -3 \\[1.1ex] 2 & 9 & 4 \end{pmatrix}=\begin{pmatrix} \bm{5} & \bm{-4} & \bm{0} \\[1.1ex] \bm{1} & \bm{3} & \bm{-3} \\[1.1ex] \bm{2} & \bm{9} & \bm{4} \end{pmatrix}$

Queste sono tutte le proprietà del prodotto di uno scalare e di una matrice, quindi questa è la fine di questo articolo. Speriamo che ti sia piaciuto e, soprattutto, che tu abbia imparato a risolvere la moltiplicazione dei numeri con le matrici.

Altre operazioni matriciali legate alla moltiplicazione, molto utili, sono invece le potenze. Qui ti lasciamo la pagina in cui imparerai cos’è e come risolvere la potenza di una matrice , nel caso fossi curioso.

Come moltiplicare un numero per una matrice?

Esempio:

Risolti i problemi di moltiplicazione di un numero per una matrice

Esercizio 1:

Esercizio 2:

Esercizio 3:

Esercizio 4:

Proprietà del prodotto di un numero per una matrice

Lascia un commento Annulla risposta