▷ Come moltiplicare i polinomi (esercizi risolti)

In questa pagina imparerai come si moltiplicano i polinomi. Potrai anche vedere esempi di moltiplicazione di polinomi e, inoltre, esercizi risolti passo dopo passo. Infine, scoprirai quali sono le proprietà della moltiplicazione dei polinomi.

Tuttavia, per comprendere appieno il concetto di moltiplicazione dei polinomi, passeremo dal più elementare al più complicato, ovvero inizieremo con come moltiplicare un polinomio per un numero, e poi vedremo come moltiplicare un polinomio per un monomio e, infine, spiegheremo come moltiplicare due o più polinomi tra loro.

Ti consiglio di seguire quest’ordine, ma se pensi di aver già padroneggiato le operazioni con i polinomi precedenti puoi passare direttamente alla moltiplicazione tra polinomi cliccando sull’indice:

Moltiplicare un polinomio per un numero

Il prodotto di uno scalare (o di un numero) e di un polinomio è abbastanza semplice da risolvere, basta moltiplicare il numero per il coefficiente di ciascun termine del polinomio .

moltiplicazione di un numero per un polinomio

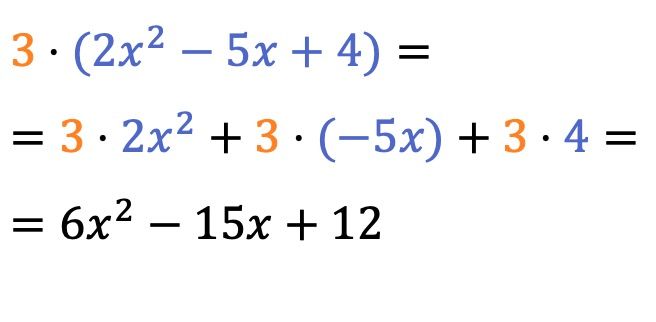
Il segno di moltiplicazione prima delle parentesi può essere omesso.

$\begin{array}{l} 2\cdot (5x^4-6x^2) = \\[2ex] =2 (5x^4-6x^2)= \\[2ex] = 10x^4-12x^2 \end{array}$

Moltiplicazione di un polinomio per un monomio

Prima di vedere come moltiplicare un polinomio per un monomio, ricordiamo innanzitutto come si moltiplicano tra loro i monomi, perché è necessario conoscerlo per poter fare questo tipo di operazione sui polinomi.

Il prodotto di due monomi consiste nel moltiplicare tra loro i loro coefficienti e tra loro le parti letterali, cioè si moltiplicano i coefficienti dei monomi e si sommano gli esponenti delle variabili che hanno la stessa base. Guarda il seguente esempio:

$3x^2 \cdot 4x^5 = (3\cdot 4) x^{2+5} = 12x^7$

Ora vediamo come moltiplicare un monomio per un polinomio:

In matematica, per risolvere la moltiplicazione di un monomio per un polinomio, il monomio viene moltiplicato per ciascun termine del polinomio.

moltiplicazione di un polinomio per un monomio

Come prima, è anche possibile omettere il segno di moltiplicazione:

$\begin{array}{l} -4x \cdot (2x^3-5x^2)= \\[2ex] =-4x (2x^3-5x^2)=\\[2ex] = -4x\cdot 2x^3 -4x \cdot (-5x^2) = \\[2ex] =-8x^4 +20x^3 \end{array}$

Nota nell’esempio precedente che quando moltiplichi monomi o polinomi devi tenere conto anche della regola dei segni. Infatti, un errore molto comune quando si moltiplicano monomi e polinomi è sbagliare il segno di un termine.

Sicuramente ad un certo punto, quando hai visto qualcosa di nuovo in matematica, ti sei chiesto: a cosa serve ? Ebbene, questo tipo di moltiplicazione serve per ottenere il fattore comune di un polinomio , operazione che permette di semplificare i polinomi (molto utile). Puoi vedere cos’è e come viene calcolato il fattore comune di un polinomio in questo link.

Moltiplicazione di due polinomi

Una volta che sappiamo come moltiplicare i polinomi per numeri e per monomi, vediamo di cosa si tratta e come moltiplicare i polinomi per polinomi.

Per moltiplicare i polinomi, attenersi alla seguente procedura:

Moltiplica ciascun termine del primo polinomio per tutti i termini del secondo polinomio.
Aggiungi (o sottrai) monomi dello stesso grado (monomi simili).

Per poter vedere esattamente in cosa consiste questo metodo, risolveremo passo dopo passo la seguente moltiplicazione di polinomi:

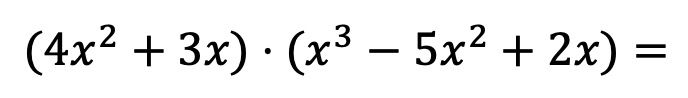
Innanzitutto dobbiamo moltiplicare ciascun elemento del primo polinomio moltiplicatore per ciascun termine del secondo polinomio:

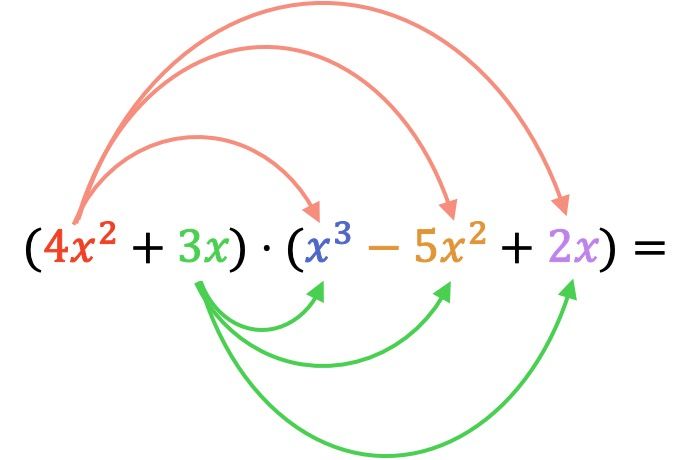
moltiplicazione di polinomi passo dopo passo

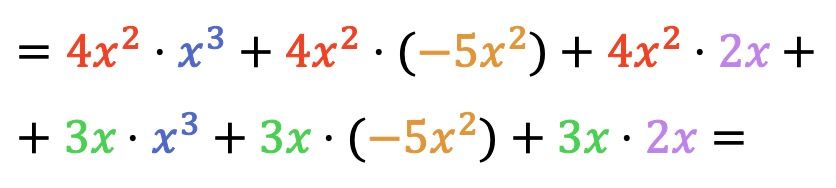
Ora eseguiamo tutte le moltiplicazioni dei monomi:

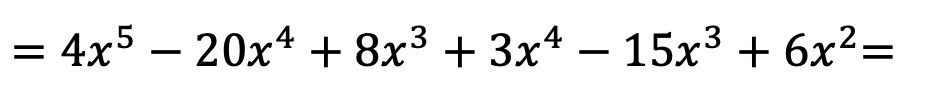
Una volta moltiplicati tra loro i polinomi, non ci resta che raggruppare i termini risultanti che sono simili, cioè i termini che hanno la stessa lettera e lo stesso esponente:

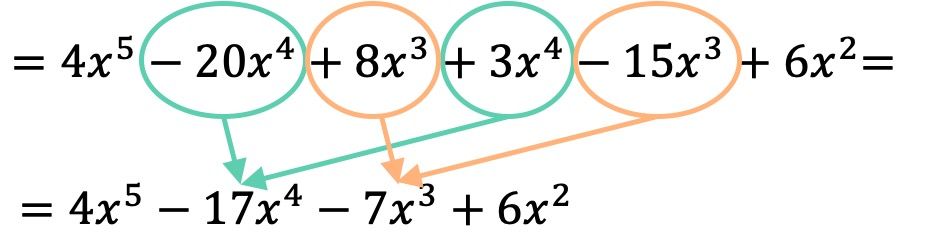
moltiplicazione di polinomi per polinomi

Il risultato della moltiplicazione polinomiale è quindi:

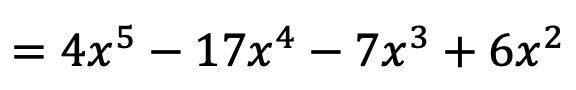
E in questo modo abbiamo già calcolato la moltiplicazione dei polinomi. Forse adesso ti sembra molto difficile, ma vedrai che quando ti eserciterai con due o tre esercizi sarà molto più semplice.

Ora che hai visto come si risolve la moltiplicazione tra due polinomi, probabilmente ti interessa sapere come dividere i polinomi . In effetti, dividere i polinomi è molto più complicato che moltiplicarli, ecco perché abbiamo spiegato la procedura (e i consigli😉) passo dopo passo in modo che tu possa comprenderla appieno. Se sei interessato, clicca su questo link per vedere come sono divisi i polinomi.

Moltiplicazione polinomiale verticale

Abbiamo appena visto come moltiplicare un polinomio per un altro polinomio in orizzontale, ma questo si può fare anche in un modo più classico: moltiplicare i polinomi in verticale. Vediamo come si utilizza questo metodo risolvendo un esempio di moltiplicazione polinomiale.

Se vogliamo moltiplicare verticalmente i seguenti due polinomi:

$(5x^2+3x-4) \cdot (2x^2-x)$

La prima cosa che dobbiamo fare è posizionare un polinomio sotto l’altro, come una moltiplicazione algebrica di polinomi:

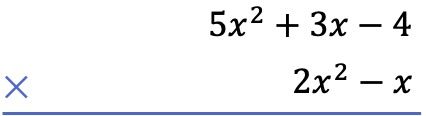
In secondo luogo, moltiplichiamo ciascun termine del polinomio riportato di seguito per ciascun termine del polinomio riportato sopra e mettiamo i risultati ordinati per colonne dal grado più alto a quello più basso:

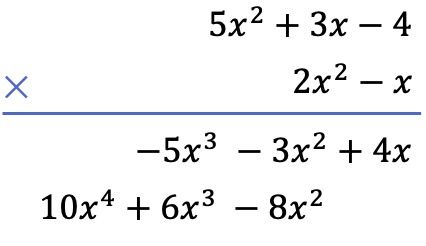
E infine, aggiungiamo i termini allineati verticalmente:

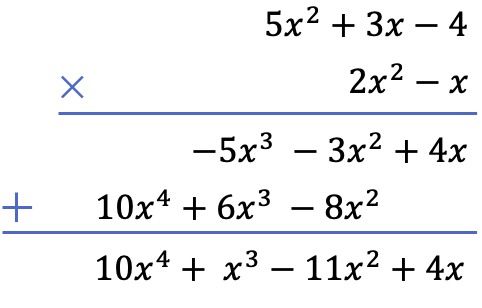
Ora che hai visto i 2 metodi esistenti per risolvere una moltiplicazione di polinomi, sapevi che puoi anche moltiplicare le frazioni con i polinomi ? E con questi tipi di frazioni è possibile eseguire non solo le moltiplicazioni, ma tutti i tipi di operazioni. Clicca questo link e scopri cosa sono le frazioni algebriche .

Proprietà della moltiplicazione polinomiale

La moltiplicazione dei polinomi ha le seguenti caratteristiche:

Proprietà commutativa : l’ordine dei polinomi moltiplicativi non modifica il risultato della moltiplicazione.

$P(x)\cdot Q(x) = Q(x) \cdot P(x)$

Proprietà associativa : quando si moltiplicano tre o più polinomi, il risultato del prodotto è lo stesso indipendentemente da come sono raggruppati i fattori:

$\bigl(P(x) \cdot Q(x)\bigr) \cdot R(x) =P(x) \cdot \bigl(Q(x) \cdot R(x)\bigr)$

Proprietà distributiva : la somma di due polinomi moltiplicata per un terzo è uguale alla somma di ciascuna addizione moltiplicata per il terzo polinomio.

$P(x)\cdot \bigl(Q(x)+ R(x)\bigr) = P(x)\cdot Q(x) + P(x) \cdot R(x)$

Il grado del polinomio risultante dalla moltiplicazione tra due polinomi è pari alla somma dei gradi dei due polinomi moltiplicati.

Esercizi risolti sulla moltiplicazione di polinomi

Affinché tu possa esercitarti, ti lascio con diversi esercizi risolti sulla moltiplicazione dei polinomi. Puoi provare a risolverli da solo e verificare i risultati con la soluzione proposta. Potete poi farci tutte le vostre domande nei commenti, saremo felici di aiutarvi.

Esercizio 1

Calcolare i seguenti prodotti tra polinomi e scalari:

$\text{A)} \ 4\cdot (2x^3-4x)$

$\text{B)} \ -3 \cdot (-5x^2+9x)$

$\text{C)} \ 5\cdot(3x^2+4x-7)$

$\text{D)} \ -6\cdot(4x^5-6x^3+8x^2-7)$

Vedi la soluzione

Per calcolare la moltiplicazione di un polinomio per un numero, è necessario moltiplicare il numero per il coefficiente di ciascun elemento del polinomio. COSÌ:

$\text{A)} \ 4\cdot (2x^3-4x) =4 \cdot 2x^3 -4\cdot 4x = \bm{8x^3-16x}$

$\text{B)} \ -3 \cdot (-5x^2+9x) = -3 \cdot (-5x^2)-3\cdot 9x = \bm{15x^2-27x}$

$\text{C)} \ 5\cdot(3x^2+4x-7) = \bm{15x^2+20x-35}$

$\text{D)} \ -6\cdot(4x^5-6x^3+8x^2-7) = \bm{-24x^5+36x^3-48x^2+42}$

Esercizio 2

Risolvi le seguenti moltiplicazioni tra polinomi e monomi:

$\text{A)} \ 2x \cdot (5x^2+3)$

$\text{B)} \ -4x^2 \cdot (6x^4-9x^2)$

$\text{C)} \ -5x^3\cdot (-2x^3+2x^2-5)$

$\text{D)} \ 3x^2\cdot(7x^6-4x^5-x^3-3x)$

Vedi la soluzione

Per risolvere la moltiplicazione di un polinomio per un monomio, devi moltiplicare detto monomio per ciascun termine del polinomio. COSÌ:

$\text{A)} \ 2x \cdot (5x^2+3) = 2x \cdot 5x^2+2x\cdot 3 = \bm{10x^3+6x}$

$\text{B)} \ -4x^2 \cdot (6x^4-9x^2)= -4x^2 \cdot 6x^4 - 4x^2 \cdot (-9x^2) = \bm{-24x^6+36x^4}$

$\text{C)} \ -5x^3\cdot (-2x^3+2x^2-5) = \bm{10x^6-10x^5+25x^3}$

$\text{D)} \ 3x^2\cdot(7x^6-4x^5-x^3-3x) = \bm{21x^8-12x^7-3x^5-9x^3}$

Esercizio 3

Determinare il risultato delle seguenti moltiplicazioni tra polinomi:

$\text{A)} \ (4x^2 + 1) \cdot (3x^2-2)$

$\text{B)} \ (-3x^4+2x) \cdot (5x^4-x)$

$\text{C)} \ (2x^3-5x^2)\cdot (4x-7)$

Vedi la soluzione

Per calcolare una moltiplicazione di due polinomi, dobbiamo moltiplicare ciascun elemento del primo polinomio per ciascun elemento del secondo polinomio e quindi raggruppare insieme i termini simili. COSÌ:

$\color{blue} \mathbf{A}\bm{)} \color{black} \ \begin{array}{l} (4x^2 + 1) \cdot (3x^2-2) = \\[2ex] =4x^2 \cdot 3x^2 +4x^2\cdot (-2) +1 \cdot 3x^2 +1 \cdot (-2) = \\[2ex] = 12x^4-8x^2+3x^2 -2 = \\[2ex] = \bm{12x^4-5x^2-2} \end{array}$

$\color{blue} \mathbf{B}\bm{)} \color{black} \ \begin{array}{l} (-3x^4+2x) \cdot (5x^4-x) = \\[2ex] =-3x^4\cdot 5x^4 -3x^4\cdot (-x) +2x \cdot 5x^4 +2x \cdot (-x) = \\[2ex] = -15x^8+3x^5+10x^5-2x^2 = \\[2ex] = \bm{-15x^8+13x^5-2x^2} \end{array}$

$\color{blue} \mathbf{C}\bm{)} \color{black} \ \begin{array}{l} (2x^3-5x^2)\cdot (4x-7) = \\[2ex] =2x^3\cdot 4x +2x^3\cdot (-7) -5x^2 \cdot 4x -5x^2\cdot (-7) = \\[2ex] = 8x^4-14x^3-20x^3+35x^2 = \\[2ex] = \bm{8x^4-34x^3+35x^2} \end{array}$

Esercizio 4

Trova il risultato delle seguenti moltiplicazioni tra polinomi:

$\text{A)} \ (4x^2-6x+2) \cdot (5x^3-x^2)$

$\text{B)} \ (3x^3-2x+7) \cdot (-4x^3+5x)$

$\text{C)} \ (9x^4-4x^3+x^2)\cdot (2x^5-4x^4-5x^3)$

Vedi la soluzione

Per calcolare una moltiplicazione di due polinomi, dobbiamo moltiplicare ciascun elemento del primo polinomio per ciascun elemento del secondo polinomio, quindi aggiungere i termini simili. COSÌ:

$\color{blue} \mathbf{A}\bm{)} \color{black} \ \begin{array}{l} (4x^2-6x+2) \cdot (5x^3-x^2) = \\[2ex] =4x^2 \cdot 5x^3 +4x^2\cdot (-x^2) -6x \cdot 5x^3 -6x \cdot (-x^2) + 2 \cdot 5x^3 +2 \cdot (-x^2) = \\[2ex] = 20x^5-4x^4-30x^4+6x^3+10x^3-2x^2 = \\[2ex] = \bm{20x^5-34x^4+16x^3-2x^2} \end{array}$

$\color{blue} \mathbf{B}\bm{)} \color{black} \ \begin{array}{l} (3x^3-2x+7) \cdot (-4x^3+5x) = \\[2ex] =3x^3 \cdot (-4x^3) +3x^3\cdot 5x -2x \cdot (-4x^3) -2x \cdot 5x + 7 \cdot (-4x^3) +7 \cdot 5x = \\[2ex] =-12x^6+15x^4+8x^4-10x^2-28x^3+35x = \\[2ex] = \bm{-12x^6+23x^4-28x^3-10x^2+35x} \end{array}$

$\color{blue} \mathbf{C}\bm{)} \color{black} \ \begin{array}{l} (9x^4-4x^3+x^2)\cdot (2x^5-4x^4-5x^3) = \\[2ex] = 18x^9-36x^8-45x^7-8x^8+16x^7+20x^6+2x^7-4x^6-5x^5 = \\[2ex] = \bm{18x^9-44x^8-27x^7+16x^6-5x^5} \end{array}$

Esercizio 5

Calcolare le seguenti moltiplicazioni di polinomi:

$\text{A)} \ (2x^4+3x^3-6x^2+5x-1) \cdot (4x^2-6x)$

$\text{B)} \ (x^2-4x+7) \cdot (-x^3-5x^2+2x+9)$

$\text{C)} \ (2x^7+6x^5+3x^4-5x^2)\cdot (4x^6-8x^3-x^2+8)$

Vedi la soluzione

Per realizzare un prodotto di 2 polinomi, devi moltiplicare ciascun termine del primo polinomio per ciascun termine del secondo polinomio, quindi raggruppare i monomi simili ottenuti. Ancora:

$\color{blue} \mathbf{A}\bm{)} \color{black} \ \begin{array}{l}(2x^4+3x^3-6x^2+5x-1) \cdot (4x^2-6x)= \\[2ex] = 8x^6-12x^5+12x^5-18x^4-24x^4+36x^3+20x^3-30x^2-4x^2+6x = \\[2ex] = \bm{8x^6-42x^4+56x^3-34x^2+6x} \end{array}$

$\color{blue} \mathbf{B}\bm{)} \color{black} \ \begin{array}{l} (x^2-4x+7) \cdot (-x^3-5x^2+2x+9)= \\[2ex] =-x^5-5x^4+2x^3+9x^2+4x^4+20x^3-8x^2-36x-7x^3-35x^2+14x+63 = \\[2ex] = \bm{-x^5-x^4+15x^3-34x^2-22x+63} \end{array}$

$\color{blue} \mathbf{C}\bm{)} \color{black} \ \begin{array}{l} (2x^7+6x^5+3x^4-5x^2)\cdot (4x^6-8x^3-x^2+8) = \\[2ex] = 8x^{13}-16x^{10}-2x^9+16x^7+24x^{11}-48x^8-6x^7+48x^5+ \\[2ex] + \ 12x^{10}-24x^7-3x^6+24x^4-20x^8+40x^5+5x^4-40x^2 = \\[2ex] = \bm{8x^{13}+24x^{11}-4x^{10}-2x^9-68x^8-14x^7-3x^6+} \\[2ex] \bm{+ \ 88x^5+29x^4-40x^2} \end{array}$

Esercizio 6

Risolvi la seguente moltiplicazione di 3 polinomi:

$(2x^2-3) \cdot (-5x^4+3x^2-6) \cdot (9x^3-6x)$

Vedi la soluzione

Il funzionamento del problema consiste in 2 moltiplicazioni di polinomi, più precisamente è composto da due binomi e un trinomio. Quindi dobbiamo prima risolvere il prodotto e poi moltiplicare il risultato per il polinomio rimanente.

Calcoliamo quindi la prima moltiplicazione:

$\begin{array}{l} (2x^2-3) \cdot (-5x^4+3x^2-6) \cdot (9x^3-6x) = \\[2ex] = \bigl[-10x^6+6x^4-12x^2+15x^4-9x^2+18 \bigr]\cdot (9x^3-6x) = \\[2ex] = (-10x^6+21x^4-21x^2+18)\cdot (9x^3-6x)\end{array}$

E ora risolviamo la restante moltiplicazione:

$\begin{array}{l} (-10x^6+21x^4-21x^2+18)\cdot (9x^3-6x)= \\[2ex] = -90x^9+60x^7+189x^7-126x^5-189x^5+126x^3+162x^3-108x \\[2ex] =\bm{-90x^9+249x^7-315x^5+288x^3-108x} \end{array}$

Esercizio 7

Moltiplicare i seguenti polinomi con coefficienti razionali (con frazioni):

$\displaystyle \left( \frac{1}{3}x^2- 4x \right) \cdot \left( 5x- \frac{2}{7} \right)$

Vedi la soluzione

Sebbene i polinomi abbiano frazioni, è pur sempre una moltiplicazione tra due polinomi. Va quindi risolto come qualsiasi prodotto polinomiale: moltiplica tutti gli elementi tra loro e poi raggruppa i monomi simili.

Moltiplichiamo quindi i polinomi:

$\displaystyle \begin{array}{l} \displaystyle\left( \frac{1}{3}x^2- 4x \right) \cdot \left( 5x- \frac{2}{7} \right) = \\[4ex] = \displaystyle\frac{1}{3}x^2 \cdot 5x +\frac{1}{3}x^2\cdot \left(- \frac{2}{7} \right) -4x \cdot 5x - 4x \cdot \left(- \frac{2}{7} \right) = \\[4ex] =\displaystyle \frac{5}{3}x^3 -\frac{2}{21}x^2 -20x^2+\frac{8}{7} x\end{array}$

E, infine, aggiungiamo (o sottraiamo) i termini le cui parti letterali sono identiche:

$\begin{array}{l}\displaystyle \frac{5}{3}x^3 -\frac{2}{21}x^2 -20x^2+\frac{8}{7} x= \\[4ex] \displaystyle= \frac{5}{3}x^3 -\frac{2}{21}x^2 -\frac{420}{21}x^2+\frac{8}{7} x \\[4ex] \displaystyle=\mathbf{\frac{5}{3}}\bm{x^3} -\mathbf{\frac{422}{20}}\bm{x^2}+\mathbf{\frac{8}{7}} \bm{x} \end{array}$

Per completare con successo questo esercizio, è importante padroneggiare le operazioni con le frazioni. Ma se hai domande su qualsiasi passaggio, puoi farle nei commenti e ti risponderemo il più rapidamente possibile.

Moltiplicazione (o prodotto) di polinomi

Moltiplicare un polinomio per un numero

Moltiplicazione di un polinomio per un monomio

Moltiplicazione di due polinomi

Moltiplicazione polinomiale verticale

Proprietà della moltiplicazione polinomiale

Esercizi risolti sulla moltiplicazione di polinomi

Esercizio 1

Esercizio 2

Esercizio 3

Esercizio 4

Esercizio 5

Esercizio 6

Esercizio 7

Lascia un commento Annulla risposta