Questa pagina spiega come moltiplicare numericamente e graficamente un vettore per un numero reale (o uno scalare). Inoltre troverai anche esempi ed esercizi risolti del prodotto di un vettore per uno scalare. Infine vengono spiegate anche le proprietà di questo tipo di operazione con i vettori.
Come si moltiplica un vettore per un numero reale?
Per calcolare numericamente il prodotto di un vettore e un numero (o uno scalare), ciascuna componente del vettore deve essere moltiplicata per il numero.
![]()
![]()
Pertanto, il risultato della moltiplicazione di un vettore per un numero dà origine a un nuovo vettore con le seguenti caratteristiche:
- Il risultato del prodotto di un vettore per uno scalare produce un nuovo vettore con la stessa direzione del vettore originale.
- Inoltre, il nuovo vettore avrà la stessa direzione se il numero è positivo.
- Oppure avrà il significato opposto se il numero è negativo.
- La grandezza del vettore risultante è equivalente alla grandezza del vettore originale moltiplicata per lo scalare.
Nel grafico seguente puoi vedere come viene mantenuta la direzione del vettore indipendentemente dal segno dello scalare. D’altra parte, la direzione del vettore dipende dal segno del numero che moltiplica.

Inoltre, nel grafico seguente si vede chiaramente che la grandezza del vettore prodotto risultante è uguale alla grandezza del vettore originale moltiplicato per lo scalare.
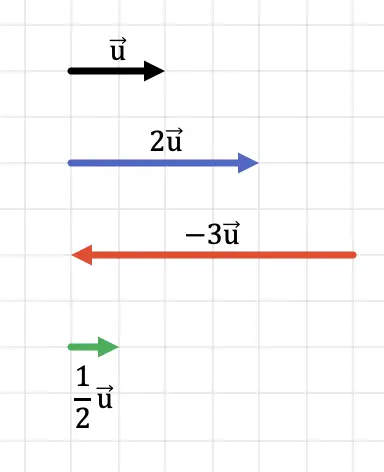
Ovviamente, se moltiplichiamo il vettore per un numero maggiore di 1, il risultato è un vettore di maggiore lunghezza (di modulo maggiore). D’altra parte, se moltiplichiamo il vettore per un numero inferiore a 1, il risultato è un vettore di lunghezza inferiore (modulo più piccolo).
Nota: non confondere il prodotto di un vettore e di uno scalare con il prodotto scalare di vettori . Sebbene abbiano un nome simile, sono due concetti completamente diversi.
Esempio di prodotto di un vettore per uno scalare
Successivamente, vedremo un esempio numerico di come viene calcolato il prodotto di un vettore e un numero:
- Moltiplicare il seguente vettore per 4:
![]()
![]()
Come hai visto, questo tipo di operazione vettoriale non è molto complicata perché non devi fare molti calcoli.
Tuttavia, esistono operazioni vettoriali più complicate, come l’addizione e la sottrazione di vettori. Se hai già capito come calcolare il prodotto di un vettore per uno scalare, ti consigliamo di passare al livello successivo e vedere come risolvere l’addizione e la sottrazione di vettori , poiché si tratta di operazioni un po’ più difficili e, in effetti, sono molto più utilizzati (sono più importanti).
Proprietà di moltiplicare un vettore per un numero
Il prodotto tra un vettore e un numero ha le seguenti proprietà:
- Proprietà associativa : quando il vettore viene moltiplicato per più di un numero, l’ordine delle moltiplicazioni non ha importanza.
![]()
- Proprietà distributiva rispetto all’addizione e alla sottrazione di vettori:
![]()
![]()
- Proprietà distributiva rispetto all’addizione di scalari:
![]()
- Elemento neutro : Ovviamente qualsiasi vettore moltiplicato per 1 dà il vettore stesso:
![]()
Risolti problemi di moltiplicazione di un vettore per uno scalare
Esercizio 1
Calcola analiticamente il risultato del prodotto del seguente vettore per 3:
![]()
Per trovare il prodotto, devi moltiplicare ciascuna coordinata del vettore per 3:
![]()
Esercizio 2
Moltiplica il seguente vettore per 6 e trova il suo modulo:
![]()
Per prima cosa moltiplichiamo il vettore per lo scalare:
![]()
Esistono ora due modi per calcolare la grandezza del vettore ottenuto. Il primo è trovare il modulo del vettore originale, quindi moltiplicarlo per 6:
![]()
![]()
E il secondo modo è calcolare direttamente la grandezza del vettore ottenuto nella moltiplicazione:
![]()
In modo che con entrambe le procedure si dimostra che il risultato non dipende dal metodo con cui viene calcolato il modulo.
Esercizio 3
Dal seguente vettore:
![]()
Calcolare algebricamente le seguenti operazioni:
![]()
![]()
![]()
![]()
Successivamente, determina se i vettori risultanti hanno la stessa direzione e direzione del vettore originale e ordinali dal più breve al più lungo.
Per prima cosa calcoliamo le moltiplicazioni:
![]()
![]()
![]()
![]()
Pertanto, i vettori moltiplicati per numeri positivi hanno la stessa direzione e direzione del vettore originale. E i vettori moltiplicati per numeri negativi hanno la stessa direzione ma la direzione opposta al vettore originale.
Vettori della stessa direzione e della stessa direzione:
![]()
E
![]()
Vettori con la stessa direzione ma significato diverso:
![]()
Infine, dobbiamo ordinare i vettori in base alla loro lunghezza o, equivalentemente, al loro modulo. Il vettore di lunghezza maggiore (o modulo più grande) sarà quello che è stato moltiplicato per un numero maggiore (in valore assoluto), e il vettore di lunghezza minore (o modulo più piccolo) sarà quello che è stato moltiplicato per un numero minore numero (in valore assoluto). Quindi l’ordine delle lunghezze è:
![]()
Si noti che la lunghezza o modulo non dipende dal segno dello scalare moltiplicato, poiché la direzione del vettore non ne modifica il modulo.
Esercizio 4
Consideriamo i due vettori seguenti:
![]()
Calcolare la seguente operazione:
![]()
Per prima cosa risolviamo le moltiplicazioni dei vettori per i numeri:
![]()
![]()
![]()
E poi sottraiamo i vettori:
![]()
![]()
Esercizio 5
Esegui le seguenti moltiplicazioni di vettori per scalari e rappresenta i risultati graficamente:
![]()
![]()
![]()
![]()
![]()
Per prima cosa moltiplichiamo i vettori per gli scalari reali:
![]()
![]()
![]()
![]()
![]()
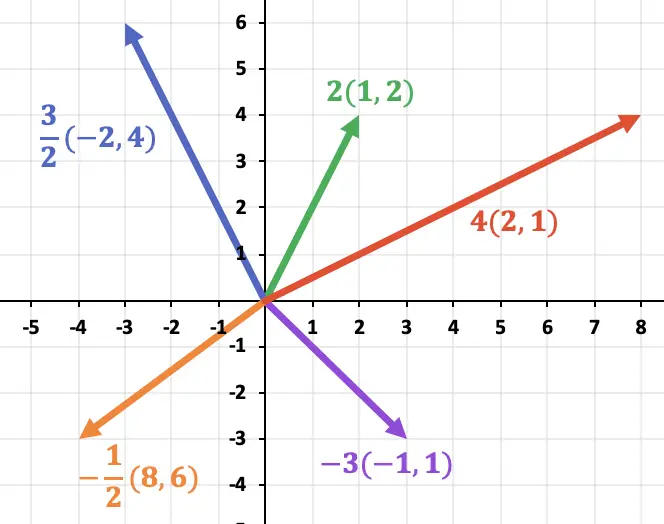
Infine, una volta calcolati i vettori, li rappresentiamo nel grafico: