Come calcolare il modulo di un vettore

In questa pagina vedrai la spiegazione della grandezza di un vettore e come calcolarlo con la sua formula. Potrai anche vedere come trovare il modulo da due punti: la sua origine e la sua fine. Inoltre, scoprirai come determinare le componenti di un vettore dal suo modulo e le proprietà del modulo di un vettore. Puoi anche esercitarti con esempi, esercizi e problemi passo passo.

Qual è il modulo di un vettore?

La grandezza di un vettore rappresenta la distanza tra la sua origine e la sua fine. Pertanto, la grandezza di un vettore è uguale alla lunghezza di detto vettore.

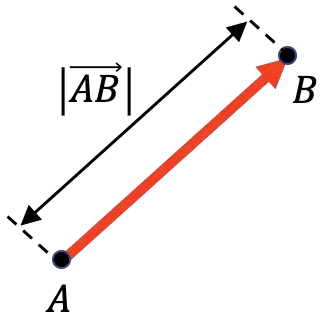
Come puoi vedere nella rappresentazione grafica sopra, la grandezza di un vettore è simboleggiata da una barra verticale su ciascun lato del vettore:

$\lvert \vv{AB}\rvert$

D’altra parte, il modulo di un vettore è uguale alla norma di un vettore , quindi puoi vederlo scritto anche in questo modo. Ecco perché ci sono matematici che rappresentano anche il modulo di un vettore con due barre verticali su ciascun lato:

$\lvert \lvert \vv{AB}\rvert\rvert$

Formula per il modulo di un vettore

Per trovare il modulo di un vettore nel piano, dobbiamo applicare la seguente formula:

Per determinare la grandezza di un vettore, dobbiamo calcolare la radice quadrata (positiva) della somma dei quadrati delle sue componenti. In altre parole, se abbiamo il seguente vettore:

$\vv{\text{u}} = (\text{u}_x,\text{u}_y)$

Il suo modulo è:

$\displaystyle \lvert \vv{\text{u}} \rvert = \sqrt{ \text{u}_x^2+\text{u}_y^2}$

Ad esempio, calcoleremo la grandezza del seguente vettore utilizzando la formula:

$\vv{\text{u}} = (4,3)$

$\lvert \vv{\text{u}} \rvert =\sqrt{4^2+3^2} = \sqrt{16+9}=\sqrt{25} = \bm{5}$

Calcola il modulo di un vettore con le coordinate della sua origine e della sua fine

Abbiamo appena visto come si determina la grandezza di un vettore quando ne conosciamo le componenti, ma cosa accadrebbe se conoscessimo solo i punti in cui inizia e dove finisce?

Pertanto, per calcolare la grandezza di un vettore dalle coordinate della sua origine e della sua fine, devi seguire questi due passaggi:

Per prima cosa troviamo le componenti del vettore. Per fare ciò, dobbiamo sottrarre l’estremo meno l’origine.
E poi calcoliamo il modulo del vettore ottenuto con la formula che abbiamo visto nella sezione precedente.

Vediamo come si realizza attraverso un esempio:

Calcolare il modulo del vettore la cui origine è il punto
$A(2,1)$

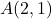
e come punto finale

$B(-1,4).$

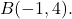
Dobbiamo prima trovare le componenti del vettore, quindi sottraiamo il suo punto finale meno la sua origine:

$\vv{AB}=B-A=(-1,4)-(2,1)=(-3,3)$

Una volta conosciuto il vettore, calcoliamo la sua magnitudo utilizzando la formula della magnitudo del vettore:

$\begin{vmatrix} \vv{AB} \end{vmatrix} =\sqrt{(-3)^2+3^2} = \sqrt{9+9}=\sqrt{18}$

E lasciamo il risultato come radice quadrata, perché non è esatto.

Come calcolare le componenti di un vettore dal suo modulo

Abbiamo visto come estrarre la grandezza di un vettore dalle sue componenti, ma il processo può anche essere inverso. In altre parole, possiamo calcolare le componenti di un vettore attraverso il suo modulo.

Il processo per trovare le componenti di un vettore dalla sua grandezza è chiamato decomposizione vettoriale . Quindi, per scomporre un vettore, abbiamo bisogno della sua grandezza, ovviamente, e dell’angolo che forma con l’asse delle ascisse (asse X).

In modo che le componenti X e Y del vettore possano essere calcolate con i rapporti trigonometrici:

Come puoi vedere nell’immagine, il modulo di un vettore forma un triangolo rettangolo con le sue componenti, quindi si possono applicare le formule elementari della trigonometria.

Bisogna tenere conto che, a differenza del modulo di un vettore, le sue componenti possono essere negative perché seno e coseno possono assumere valori negativi.

Ad esempio, risolveremo la scomposizione vettoriale del vettore il cui modulo e angolo con l’asse OX sono:

$\lvert \vv{\text{u}} \rvert = 10 \qquad \alpha = 60º$

La componente orizzontale del vettore è uguale al modulo moltiplicato per il coseno dell’angolo:

$\text{u}_x= \lvert \vv{\text{u}}\rvert \cdot \text{cos}(60º)= 10 \cdot 0,5 = 5$

E la componente verticale del vettore è uguale a moltiplicare il modulo per il seno dell’angolo:

$\text{u}_y= \lvert \vv{\text{u}}\rvert \cdot \text{sen}(60º)= 10 \cdot 0,87 = 8,7$

Quindi il vettore è il seguente:

$\vv{\mathbf{u}}\bm{ = (5 \ ,\ 8,7)}$

Proprietà del modulo di un vettore

Il modulo è un tipo di operazione vettoriale che presenta le seguenti caratteristiche:

La grandezza di un vettore non può mai essere negativa , sarà sempre uguale o maggiore di 0.

$\lvert \vv{\text{u}} \rvert \geq 0$

Infatti, l’unico vettore che esiste con magnitudo zero è il vettore zero, cioè il vettore

$\vv{\text{u}}= (0,0) .$

La grandezza del prodotto di un vettore per un numero reale (o uno scalare) equivale a moltiplicare il valore assoluto dello scalare per la grandezza del vettore. Vale quindi la seguente uguaglianza:

$\lvert k \cdot \vv{\text{u}} \rvert = \lvert k \rvert \cdot \lvert \vv{\text{u}} \rvert$

La disuguaglianza triangolare è verificata: il modulo della somma di due vettori è inferiore o uguale alla somma dei loro moduli separatamente.

$\lvert \vv{\text{u}}+\vv{\text{v}} \rvert \leq \lvert\vv{\text{u}} \rvert+\lvert\vv{\text{v}} \rvert$

Inoltre, l’entità della somma di due vettori è correlata al prodotto scalare dalla seguente equazione:

$\lvert \vv{\text{u}}+\vv{\text{v}} \rvert = \sqrt{\lvert \vv{\text{u}} \rvert ^2+\lvert \vv{\text{v}} \rvert ^2 +2\cdot \vv{\text{u}}\cdot \vv{\text{v}} \vphantom{\sqrt{x^2}}}$

vettore unitario

In matematica, un vettore unitario è un vettore il cui modulo è uguale a uno.

$\lvert \vv{\text{u}} \rvert=1$

Pertanto, la lunghezza di un vettore unitario è una unità.

Può sembrare molto difficile che un vettore abbia un modulo esattamente pari a 1, ma in realtà è facile trovare questo tipo di vettore:

Per trovare il vettore unitario di qualsiasi vettore, dividilo semplicemente per il suo modulo:

$\vv{\text{v}}_u = \cfrac{\vv{\text{v}}}{\lvert \vv{\text{v}} \rvert}$

Oro

$\vv{\text{v}}_u$

è il vettore unitario di

$\vv{\text{v}},$

$\lvert \vv{\text{v}} \rvert$

il tuo modulo.

Il vettore unitario è anche chiamato versore o vettore normalizzato.

Inoltre, il vettore unitario ha la stessa direzione e direzione del vettore originale.

Ad esempio, calcoleremo il vettore unitario del seguente vettore:

$\vv{\text{v}}=(1,-1)$

Per normalizzare il vettore, dobbiamo prima calcolare la sua grandezza:

$\lvert \vv{\text{v}} \rvert=\sqrt{1^2+(-1)^2} = \sqrt{2}$

E, infine, calcoliamo il vettore unitario dividendo il vettore originale per il suo modulo:

$\displaystyle \vv{\text{v}}_u = \cfrac{\vv{\text{v}}}{\lvert \vv{\text{v}} \rvert} = \frac{(1,-1)}{\sqrt{2}}= \bm{\left(\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}} \right)}$

Esercizi del modulo vettoriale risolti

Esercizio 1

Calcolare il modulo del seguente vettore:

$\vv{a}=(6,8)$

vedi soluzione

Per calcolare il modulo del vettore dobbiamo applicare la sua formula:

$\lvert\vv{a} \rvert= \sqrt{6^2+8^2} =\sqrt{36+64} = \sqrt{100} = \bm{10}$

Esercizio 2

Ordina i seguenti vettori dal più corto al più lungo.

$\vv{a}=(4,-2)$

$\vv{b}=(3,1)$

$\vv{c}=(5,12)$

$\vv{d}=(-6,-3)$

vedi soluzione

La lunghezza di un vettore è uguale alla sua grandezza. Pertanto, dobbiamo calcolare i moduli di tutti i vettori:

$\left|\vv{a}\right|= \sqrt{4^2+(-2)^2} =\sqrt{16+4} = \sqrt{20}$

$|\vv{b}|= \sqrt{3^2+1^2} =\sqrt{9+1} = \sqrt{10}$

$\begin{vmatrix}\vv{c}\end{vmatrix}= \sqrt{5^2+12^2} =\sqrt{25+144} = \sqrt{169} = 13$

$|\vv{d}| = \sqrt{(-6)^2+(-3)^2} =\sqrt{36+9} = \sqrt{45}$

Pertanto, i vettori ordinati dalla lunghezza (o modulo) più piccola a quella più grande sono:

$|\vv{b}|< \begin{vmatrix}\vv{a}\end{vmatrix} < |\vv{d}| < \begin{vmatrix}\vv{c}\end{vmatrix}$

Esercizio 3

Determinare il modulo del vettore la cui origine è il punto

$A(-3,2)$

e come punto finale

$B(7,-4).$

vedi soluzione

Per calcolare il suo modulo, devi prima trovare il vettore. Per fare ciò, sottraiamo l’estremo meno l’origine:

$\vv{AB}=B-A=(7,-4)-(-3,2)=(10,-6)$

Una volta conosciuto il vettore, il suo modulo viene calcolato utilizzando la formula del modulo:

$\begin{vmatrix} \vv{AB} \end{vmatrix} =\sqrt{10^2+(-6)^2} = \sqrt{100+36}=\bm{\sqrt{136}}$

Esercizio 4

Scomponi il seguente vettore e trova le sue componenti:

$\lvert \vv{a} \rvert =8 \qquad \alpha = 45º$

vedi soluzione

La componente orizzontale del vettore è uguale al modulo moltiplicato per il coseno dell’angolo:

$a_x= \lvert \vv{a}\rvert \cdot \text{cos}(45º)= 8 \cdot 0,71 = 5,66$

E la componente verticale del vettore è uguale a moltiplicare il modulo per il seno dell’angolo:

$a_y= \lvert \vv{a}\rvert \cdot \text{sen}(45º)= 8 \cdot 0,71 = 5,66$

Quindi il vettore è il seguente:

$\vv{\mathbf{u}}\bm{ = (5,66 \ ,\ 5,66)}$

In questo caso le due componenti sono identiche, cioè l’angolo di inclinazione del vettore è di 45º.

Esercizio 5

Calcola il vettore con la stessa direzione e direzione del vettore successivo ma con modulo 1.

$\vv{a} = (-4,3)$

vedi soluzione

Il vettore con la stessa direzione e la stessa direzione ma con modulo 1 è il versore unitario. Per calcolarlo troviamo innanzitutto il modulo del vettore:

$\lvert \vv{a} \rvert=\sqrt{(-4)^2+3^2} = \sqrt{16+9} = \sqrt{25} = 5$