Il metodo dei minimi quadrati è uno strumento matematico per trovare la migliore retta corrispondente a un insieme di punti . Te lo spieghiamo in modo semplice:
Immagina di avere un mucchio di punti su un grafico sparsi qua e là. Vuoi trovare una linea retta che “si adatti” meglio a questi punti, in modo da ridurre al minimo la distanza tra la linea e i punti . Questa è l’idea alla base del metodo dei minimi quadrati.
Il metodo utilizza una formula per calcolare l’equazione della retta che minimizza la somma dei quadrati delle differenze tra i punti e la retta. Cerca cioè la linea che ha la “deviazione” minore dai punti.
In termini semplici, il metodo dei minimi quadrati è utile per l’analisi dei dati ottenuti durante un’indagine, con l’obiettivo di esprimere il loro comportamento in modo lineare, riducendo gli errori delle informazioni rubate.
Chi ha creato il metodo dei minimi quadrati?
Il metodo dei minimi quadrati, uno strumento fondamentale nella statistica e nell’analisi dei dati, è attribuito al matematico tedesco Carl Friedrich Gauss , che lo propose nel 1794. Tuttavia, Gauss lo pubblicò solo nel 1809 .
È interessante notare che il matematico francese Andrien-Marie Legendre pubblicò una versione simile nel 1805 , sviluppandola in modo indipendente.
Entrambi i matematici hanno contribuito a creare questo metodo che è stato ampiamente utilizzato in varie discipline per adattare i modelli ai dati osservati e fare previsioni accurate.
Formula dei minimi quadrati
Senza dubbio, per capire cosa comporta questo metodo, è essenziale spiegare la sua formula e il processo della sua attuazione. Ecco una spiegazione dettagliata della formula dei minimi quadrati:
definisci il problema
Supponiamo che tu abbia un set di dati con due variabili, una variabile indipendente (x) e una variabile dipendente (y) e desideri adattare una linea retta a questi dati.
L’obiettivo è trovare i valori dei coefficienti dell’equazione della retta (intercetta e pendenza) che minimizzi la somma dei quadrati delle differenze tra i valori reali di y, e i valori previsti dalla linea attrezzata.
Calcola l’equazione della retta
L’equazione di una retta ha la forma y = mx + b, dove m è la pendenza e b è l’intercetta y. La formula dei minimi quadrati per calcolare i valori myb è:
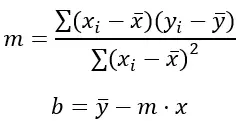
Oro:
Σ rappresenta la somma dei valori.
x i e y i sono i valori delle variabili x e y rispettivamente per ciascun punto dati.
x̄ e ȳ sono le medie dei valori rispettivamente di x e y.
(x i – x̄) e (y i – ȳ) sono le differenze tra i valori di x e y e le rispettive medie.
(x i – x̄) 2 è il quadrato della differenza tra il valore di x e la sua media.
interpretare i risultati
Una volta calcolati i valori di m e b tramite la formula, puoi utilizzarli per ottenere l’equazione della retta stimata. Ad esempio, se hai m = 2 e b = 3, l’equazione della retta adattata sarà y = 2x + 3. Ciò consente di fare previsioni o stime dei valori di y per diversi valori di x sulla base del diritto rettificato.
Quando viene utilizzato il metodo dei minimi quadrati?
Probabilmente ti chiederai: quando viene utilizzato questo metodo? È molto utile in varie situazioni! Ad esempio, quando desideri analizzare dati sperimentali o di ricerca per trovare una relazione o una tendenza .
Supponiamo che tu stia indagando sulla relazione tra il prezzo di una casa e la sua dimensione in metri quadrati. Puoi utilizzare il metodo dei minimi quadrati per trovare la linea retta che meglio si adatta ai dati e ti dà un’idea chiara di questa relazione.
Viene utilizzato anche in economia per modellare e prevedere variabili come la domanda di prodotti o il comportamento dei prezzi . Inoltre, in ingegneria, il metodo dei minimi quadrati viene applicato per adattare modelli matematici ai dati di test o simulazione.
Il metodo dei minimi quadrati è uno strumento potente e versatile che viene utilizzato in molti campi di studio e di lavoro per analizzare dati e trovare relazioni importanti.
Applicazioni del metodo dei minimi quadrati ad altri teoremi
Oltre al suo utilizzo in sé, il metodo dei minimi quadrati è molto utile in altri teoremi. Vediamo un po’ di più sull’argomento, di seguito.
Teorema di regressione
È ampiamente utilizzato nel teorema di regressione per trovare la linea migliore che si adatta a un insieme di dati . Ad esempio, puoi usarlo per analizzare la relazione tra l’altezza di una pianta e la quantità di luce che riceve per determinare come crescerà la pianta in diverse condizioni di illuminazione.
Interpolazione del teorema
In questo caso, il metodo dei minimi quadrati viene applicato anche nel teorema dell’interpolazione per trovare la funzione polinomiale che meglio si adatta a un insieme di punti. Ad esempio, puoi usarlo per approssimare la traiettoria di un oggetto in movimento in base ai dati di posizione e tempo.
Teorema dell’adattamento della curva
Viene utilizzato nel teorema dell’adattamento della curva per trovare una curva che si adatta a un insieme di dati . Ciò è utile in applicazioni come la modellazione dei dati climatici per prevedere il cambiamento climatico o per prevedere la traiettoria di un proiettile.
Teorema dell’analisi di Fourier
Nel teorema dell’analisi di Fourier, il metodo dei minimi quadrati viene utilizzato per approssimare una funzione periodica da una serie di dati discreti . Ciò vale per la segnalazione dei dati e la compressione di immagini e suoni.
Teorema della regressione non lineare
Infine, il metodo dei minimi quadrati viene applicato anche nel teorema della regressione non lineare per trovare la curva migliore che si adatta a un insieme di dati che non segue una relazione lineare . Ad esempio, puoi usarlo per analizzare in che modo la concentrazione di una sostanza chimica influisce sulla velocità di reazione.
Esempio del metodo dei minimi quadrati
Per comprendere meglio come applicare il metodo dei minimi quadrati, diamo un’occhiata all’esempio seguente.
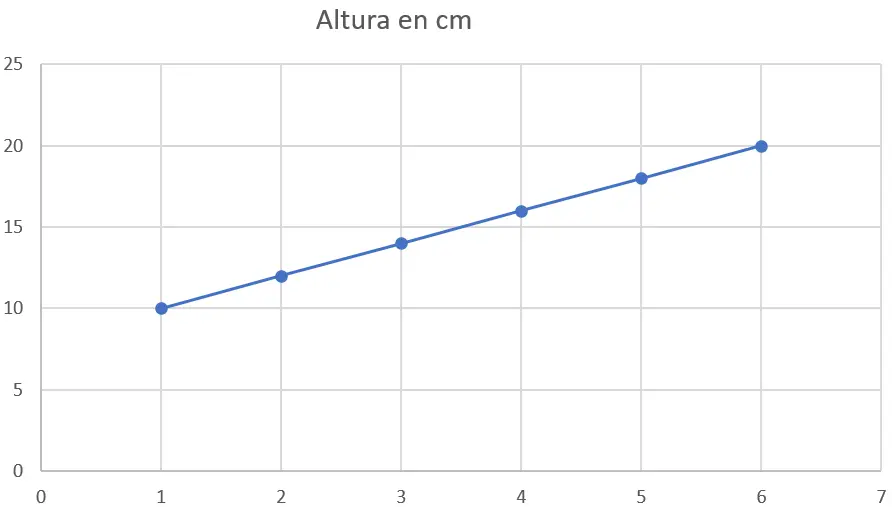
Supponiamo di avere i seguenti dati di altezza (in centimetri) di una pianta in diverse settimane:
| Settimana | altezza in centimetri |
| 1 | dieci |
| 2 | 12 |
| 3 | 14 |
| 4 | 16 |
| 5 | 18 |
| 6 | venti |
Vuoi trovare la linea retta migliore che si adatti a questi dati per fare una previsione dell’altezza futura delle piante.
Passaggio 1 : rappresentare graficamente i dati
La prima cosa da fare è tracciare i dati su un grafico a dispersione. L’asse x rappresenterà le settimane e l’asse y rappresenterà l’altezza in centimetri. Ecco il grafico:
Passaggio 2 : applicare il metodo dei minimi quadrati
Il metodo dei minimi quadrati cerca di trovare una linea che minimizzi la somma dei quadrati delle differenze tra i dati effettivi e i valori previsti dalla linea. In questo caso, la linea è rappresentata dall’equazione di una linea: y = mx + b, dove “y” è l’altezza, “x” sono le settimane, “m” è la pendenza della linea e “b” è l’intercetta y.
Per trovare i valori di “m” e “b” che minimizzino la somma dei quadrati delle differenze si utilizzano le seguenti formule:
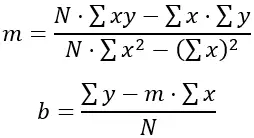
Dove N è il numero di punti dati (in questo caso, 6), Σxy è la somma delle settimane per le altezze, Σx è la somma delle settimane, Σy è la somma delle altezze e Σx 2 è la somma dei quadrati delle settimane .
Applicando queste formule ai dati di altezza, otteniamo:
Σxy = 1 10 + 2 12 + 3 14 + 4 16 + 5 18 + 6 20 = 630
Σx = 1 + 2 + 3 + 4 + 5 + 6 = 21
Σy = 10 + 12 + 14 + 16 + 18 + 20 = 90
Σx 2 = 1 2 + 2 2 + 3 2 + 4 2 + 5 2 + 6 2 = 91
Sostituendo questi valori nelle formule per “m” e “b”:
m = (6 · 630 – 21 · 90) ÷ (6 · 91 – 21 2 ) ≈ 2,07
b = (90 – 2,07 · 21) ÷ 6 ≈ 3,24
Pertanto l’equazione della retta che corrisponde al dato di altezza è: y.