Matrice unitaria

In questa pagina spieghiamo cos’è la matrice unitaria e, inoltre, la illustriamo con diversi esercizi in modo che sia ben compresa. Scoprirai inoltre quali sono tutte le proprietà di questo tipo di matrice così importante per l’algebra lineare.

Cos’è una matrice unitaria?

La definizione di matrice unitaria è la seguente:

Una matrice unitaria è una matrice complessa che moltiplicata per la sua matrice di trasposizione coniugata è uguale alla matrice identità. Cioè, è soddisfatta la seguente condizione:

U\cdot U^* = U^* \cdot U =I

Oro

U

è una matrice unitaria e

U^*

la sua trasposizione coniugata.

Pertanto, questa condizione implica che l’inversa di una matrice unitaria sia la sua trasposta coniugata , perché, secondo la definizione di matrice inversa, una matrice è l’inversa di un’altra se il suo prodotto è equivalente alla matrice d’identificazione .

\left.\begin{array}{c} U \cdot U^* =I \\[2ex] U \cdot U^{-1} = I\end{array} \right\} \longrightarrow \ U^*=U^{-1}

Pertanto una matrice unitaria sarà sempre una matrice regolare o non degenere , poiché avrà sempre un’inversa.

D’altra parte, l’analogo di una matrice unitaria in un ambiente di numeri reali è la matrice ortogonale , e in questo caso è vero che la matrice unitaria moltiplicata per la sua trasposta è uguale alla matrice identità.

U\cdot U^t = U^t \cdot U =I

Quindi in questo caso la matrice inversa di U sarebbe direttamente la sua matrice trasposta (o trasposta).

Esempi di matrici unitarie

Esempio di matrice unitaria di dimensione 2×2

Una volta visto il concetto di matrice unitaria, vedremo un esempio di matrice unitaria 2×2 per capirlo bene:

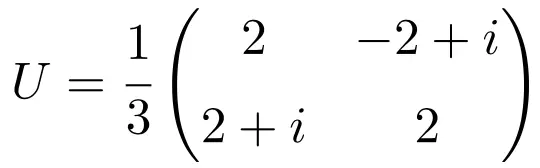
esempio di matrice unitaria di dimensione 2x2

Questa matrice è unitaria perché la moltiplicazione di se stessa per la sua matrice coniugata dà la matrice Identità (o Unità):

\displaystyle U\cdot U^*=\cfrac{1}{3} \begin{pmatrix} 2 & -2+i \\[1.1ex] 2+i & 2 \end{pmatrix}\cdot \cfrac{1}{3} \begin{pmatrix} 2 & 2-i \\[1.1ex] -2-i & 2 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}

E, come abbiamo visto in precedenza, qualsiasi matrice unitaria è commutabile con la sua trasposta coniugata:

\displaystyle U^*\cdot U=\cfrac{1}{3} \begin{pmatrix} 2 & 2-i \\[1.1ex] -2-i & 2 \end{pmatrix}\cdot \cfrac{1}{3} \begin{pmatrix} 2 & -2+i \\[1.1ex] 2+i & 2 \end{pmatrix} = \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}

Esempio di matrice diagonale unitaria

Anche la matrice diagonale composta solo dal numero complesso i è un esempio di matrice unitaria, indipendentemente dalla dimensione della matrice. Di seguito è riportato un esercizio risolto che illustra questo con una matrice unitaria di dimensione 3 × 3:

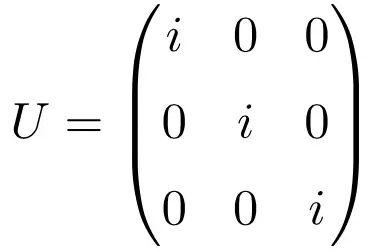
esempio di matrice unitaria di dimensione 3x3

Si noti che se risolviamo il prodotto della matrice mediante la sua trasposizione coniugata, si ottiene come soluzione la matrice Identità:

\displaystyle U\cdot U^* =\begin{pmatrix} i & 0 & 0 \\[1.1ex] 0 & i & 0 \\[1.1ex] 0& 0 & i \end{pmatrix}\cdot \begin{pmatrix} -i & 0 & 0 \\[1.1ex] 0 & -i & 0 \\[1.1ex] 0& 0 & -i \end{pmatrix}=\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0& 0 & 1 \end{pmatrix}

E la stessa cosa accade se moltiplichiamo le matrici al contrario:

\displaystyle U^*\cdot U =\begin{pmatrix} -i & 0 & 0 \\[1.1ex] 0 & -i & 0 \\[1.1ex] 0& 0 & -i \end{pmatrix}\cdot \begin{pmatrix} i & 0 & 0 \\[1.1ex] 0 & i & 0 \\[1.1ex] 0& 0 & i \end{pmatrix}=\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0& 0 & 1 \end{pmatrix}

La caratteristica di questa matrice è che serve come esempio di matrice unitaria di qualsiasi dimensione, poiché ogni volta che la matrice è formata dal numero immaginario i sulla diagonale principale e il resto degli elementi sono zero (0 ) sarà una matrice unitaria.

Proprietà di una matrice unitaria

Le proprietà delle matrici unitarie sono le seguenti:

  • Ovviamente qualsiasi matrice unitaria è una matrice normale . Sebbene non tutte le matrici normali siano matrici unitarie.
  • Tutte le matrici unitarie sono diagonalizzabili, cioè possono essere trasformate in matrici diagonali.
  • Il valore assoluto del determinante di una matrice unitaria è sempre pari a 1.

\begin{vmatrix} det(U) \end{vmatrix} = 1

  • La matrice identica è una matrice unitaria.
  • per tutti

    n

    , l’insieme di tutte le matrici unitarie

    n\times n

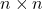
    con l’operazione prodotto matrice, formano un gruppo, detto gruppo unitario.

  • In modo che la moltiplicazione di due matrici unitarie dello stesso ordine dà un’altra matrice unitaria.
  • Il modulo di tutti gli autovalori (o autovalori) di una matrice unitaria è sempre uguale a 1.

\begin{vmatrix} \lambda \end{vmatrix} = 1

  • Gli autospazi di questo tipo di matrice sono ortogonali.

Lascia un commento

Il tuo indirizzo email non sarà pubblicato. I campi obbligatori sono contrassegnati *

Torna in alto