Matrice triangolare superiore ed inferiore

In questa pagina vedrai cos’è una matrice triangolare e i diversi tipi di matrici triangolari insieme ad esempi. Inoltre, troverai come calcolare il determinante di una matrice triangolare e quali sono le proprietà di questa matrice molto interessante. Infine, spieghiamo anche cos’è una matrice di Hessenberg, poiché è una matrice correlata alle matrici triangolari.

Cos’è una matrice triangolare?

Definizione di matrice triangolare:

Una matrice triangolare è una matrice quadrata in cui tutti gli elementi sopra o sotto la diagonale principale sono zero (0).

Le matrici triangolari sono ampiamente utilizzate nei calcoli di algebra lineare, perché invertire una matrice triangolare, calcolarne il determinante o anche risolvere sistemi di equazioni lineari con questo tipo di matrici è molto più semplice che con matrici che hanno elementi diversi da 0 in tutte le posizioni. .

matrice triangolare superiore

Una matrice triangolare superiore è una matrice quadrata i cui elementi sotto la diagonale principale sono zero (0).

Esempio di matrice triangolare superiore:

matrice triangolare inferiore

Una matrice triangolare inferiore è una matrice quadrata che ha uno zero (0) in ogni elemento che si trova sopra la diagonale principale.

Esempio di matrice triangolare inferiore:

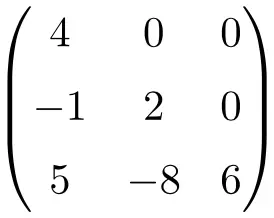
Talvolta queste matrici vengono chiamate anche con la lettera U, per la matrice triangolare superiore, e con la lettera L, per quella triangolare inferiore. Sebbene questa nomenclatura sia utilizzata principalmente in inglese, infatti la U sta per matrice triangolare superiore e la L per matrice triangolare inferiore .

Esempi di matrici triangolari

Matrice triangolare 2 × 2 dimensionale

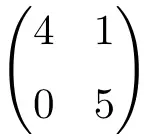
Esempio di matrice triangolare superiore 2x2

Matrice triangolare di ordine 3×3

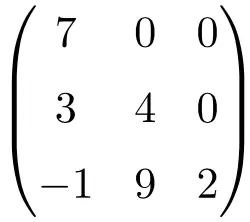
Esempio di matrice triangolare inferiore 3x3

matrice triangolare di dimensione 4×4

Esempio di matrice triangolare superiore 4x4

Determinante di una matrice triangolare

Il determinante di una matrice triangolare , sia essa triangolare superiore o inferiore, è il prodotto degli elementi sulla diagonale principale.

Dai un’occhiata al seguente esercizio risolto come sia sufficiente calcolare la moltiplicazione degli elementi della diagonale principale della matrice triangolare per trovarne il determinante:

$\displaystyle \begin{vmatrix} 2 & 5 & -6 \\[1.1ex] 0 & 4 & 9 \\[1.1ex] 0 & 0 & 3 \end{vmatrix} = 2 \cdot 4 \cdot 3 = \bm{24}$

Questo teorema è facilmente dimostrabile: basta calcolare il determinante di una matrice triangolare per blocchi (o cofattori). Questa dimostrazione è dettagliata di seguito utilizzando una matrice triangolare generica:

$\begin{aligned} \begin{vmatrix} a & b & c \\[1.1ex] 0 & d & e \\[1.1ex] 0 & 0 & f \end{vmatrix}& = a \cdot \begin{vmatrix} d & e \\[1.1ex] 0 & f \end{vmatrix} - b \cdot \begin{vmatrix} 0 & e \\[1.1ex] 0 & f \end{vmatrix} + c \cdot \begin{vmatrix} 0 & d \\[1.1ex] 0 & 0 \end{vmatrix} \\[2ex] & =a \cdot (d\cdot f) - b \cdot 0 + c \cdot 0 \\[2ex] & = a \cdot d \cdot f \end{aligned}$

Sappiamo invece che una matrice è invertibile se il suo determinante è diverso da 0. Quindi, se nessun elemento sulla diagonale principale è 0, anche la matrice triangolare sarà invertibile e, di conseguenza, sarà una matrice regolare matrice.

Proprietà della matrice triangolare

Vediamo ora quali sono le proprietà delle matrici triangolari:

Il prodotto di due matrici triangolari superiori è uguale a una matrice triangolare superiore. E viceversa: moltiplicando due matrici triangolari inferiori si ottiene un’altra matrice triangolare inferiore.

$\begin{pmatrix} 3 & 1 & 4 \\[1.1ex] 0 & -1 & 2 \\[1.1ex] 0 & 0 & 5 \end{pmatrix} \cdot \begin{pmatrix} 6 & 2 & 1 \\[1.1ex] 0 & 3 & 5 \\[1.1ex] 0 & 0 & 9 \end{pmatrix} = \begin{pmatrix}18&9&44\\[1.1ex] 0&-3&13\\[1.1ex]0&0&45\end{pmatrix}$

La trasposizione di una matrice triangolare superiore è una matrice triangolare inferiore, e viceversa: la trasposizione di una matrice triangolare inferiore è una matrice triangolare superiore.

$\left.\begin{pmatrix} 1 & 2 & 6 & 3 \\[1.1ex] 0 & 9 & 4 & 1 \\[1.1ex] 0 & 0 & -2 & 8 \\[1.1ex] 0 & 0 & 0 & 7 \end{pmatrix}\right.^{\bm{t}} = \begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex] 2 & 9 & 0 & 0 \\[1.1ex] 6 & 4 & -2 & 0 \\[1.1ex] 3 & 1 & 8 & 7 \end{pmatrix}$

Una matrice triangolare è invertibile se tutti i suoi elementi sulla diagonale principale sono diversi da zero, cioè diversi da zero. In tal caso, l’inverso di una matrice triangolare superiore (inferiore) è anche una matrice triangolare superiore (inferiore).

$\left. \begin{pmatrix}1&0&0\\[1.1ex] -3&2&0\\[1.1ex] 2&4&3\end{pmatrix} \right.^{-1} =\begin{pmatrix}1&0&0\\[1.1ex] \frac{3}{2}&\frac{1}{2}&0\\[1.1ex] -\frac{8}{3}&-\frac{2}{3}&\frac{1}{3}\end{pmatrix}$

Inoltre, la diagonale principale della matrice invertita conterrà sempre gli inversi degli elementi della diagonale principale della matrice triangolare originale.

Qualsiasi matrice diagonale è sia una matrice triangolare superiore che una matrice triangolare inferiore, ad esempio:

$\begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 8 & 0 \\[1.1ex] 0 & 0 & -2 \end{pmatrix}$

Quindi una matrice scalare è anche una matrice triangolare superiore e inferiore. Ad esempio la matrice identità:

$\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

Ovviamente la matrice zero è anche una matrice triangolare superiore ed inferiore, perché gli elementi sopra e sotto la diagonale principale sono 0:

$\begin{pmatrix} 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \end{pmatrix}$

Gli autovalori (o autovalori) di una matrice triangolare sono gli elementi della diagonale principale.

$\begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 1 & 3 & 0 \\[1.1ex] 2 & 6 & -2 \end{pmatrix} \longrightarrow \ \lambda = -2 \ ; \ \lambda = 3 \ ; \ \lambda = 5$

Una matrice triangolare superiore o inferiore è sempre in grado di diagonalizzare su base di autovettori (o autovettori).

Qualsiasi matrice può essere fattorizzata nel prodotto di una matrice triangolare inferiore e di una matrice triangolare superiore . Cioè, qualsiasi matrice può essere trasformata in una moltiplicazione di matrici triangolari. Inoltre, se la matrice è invertibile, questa trasformazione è unica. Per fattorizzare una matrice viene spesso utilizzato il metodo di scomposizione LU.

Triangolarizzare una matrice

Esistono diversi teoremi sulle matrici che possono essere triangolarizzate cambiando la base. Qui però vedremo come triangolare una matrice applicando trasformazioni elementari sulle rette , come nel metodo di Gauss.

Per esempio:

$\begin{pmatrix} 1 & 2 & 4 \\[1.1ex] 2 & -3 & 5 \\[1.1ex]1 & -1 & 6 \end{pmatrix} \begin{array}{c} \\[1.1ex] \xrightarrow{f_2 -2f_1}\\[1.1ex] \xrightarrow{f_3 -f_1} \end{array} \begin{pmatrix} 1 & 2 & 4 \\[1.1ex] 0 & -7 & -3 \\[1.1ex] 0 & -3 & 2 \end{pmatrix}\begin{array}{c} \\[1.1ex]\\[1.1ex] \xrightarrow{7f_3 -3f_2} \end{array} \begin{pmatrix} 1 & 2 & 4 \\[1.1ex] 0 & -7 & -3 \\[1.1ex] 0 & 0 & 23 \end{pmatrix}$

E in questo modo abbiamo già triangolarizzato la matrice originaria.

Ricordiamo che le trasformazioni elementari autorizzate tra linee nel metodo gaussiano sono:

Sostituisci una linea con la combinazione lineare di altre linee.
Moltiplica o dividi tutti i termini di una riga per un numero diverso da 0.
Modifica righe ordine.

Matrice di Hessenberg

La definizione della matrice di Hessenberg è la seguente:

La matrice di Hessenberg è una matrice “quasi” triangolare, vale a dire che tutti i suoi elementi sono nulli a partire dalla prima subdiagonale (matrice di Hessenberg superiore) o dalla prima superdiagonale (matrice di Hessenberg inferiore).

Sono sicuro che sia meglio compreso con un esempio di matrice di Hessenberg superiore e un altro esempio di matrice di Hessenberg inferiore:

Matrice di Hessenberg superiore

$\left.\begin{pmatrix} 3 & 5 & 1 & 4 \\[1.1ex] 8 & 2 & 7 & 1 \\[1.1ex] 0 & 6 & 3 & 5 \\[1.1ex] 0 & 0 & 1 & 9 \end{pmatrix}$

Matrice di Hessenberg inferiore

$\left.\begin{pmatrix} 2 & 4 & 0 & 0 \\[1.1ex] 1 & 9 & 6 & 0 \\[1.1ex] 3 & 5 & 1 & 2 \\[1.1ex] 8 & 2 & 3 & 7 \end{pmatrix}$

Una matrice che è sia una matrice di Hessenberg superiore che una matrice inferiore è una matrice tridiagonale .

Questa matrice prende il nome da Karl Hessenberg, un eminente ingegnere e matematico tedesco del 20° secolo.

Infine, questo tipo di matrice ha la particolarità che se viene moltiplicata per una matrice triangolare, il risultato è sempre una matrice di Hessenberg.

Matrice triangolare superiore e inferiore