Matrice singolare o degenere

In questa pagina vedrai cosa significa per una matrice essere singolare o degenere. Inoltre, ti mostriamo diversi esempi per non farti avere dubbi e, infine, ti spieghiamo tutte le proprietà di questo tipo di matrice.

Cos’è una matrice singolare o degenere?

La definizione di matrice singolare, detta anche matrice degenere, è la seguente:

Una matrice singolare o degenere è una matrice quadrata che non può essere invertita e quindi il suo determinante è uguale a 0.

Quindi, per sapere quando una matrice è singolare, è sufficiente calcolarne il determinante: se il risultato è 0, la matrice è singolare, se invece il determinante è diverso da 0, la matrice non è singolare .

Se vuoi saperne di più sulla matrice inversa, puoi consultare questa pagina dove viene spiegato in dettaglio come invertire una matrice utilizzando il metodo di Gauss , troverai anche diversi esempi ed esercizi risolti passo passo per esercitarti.

D’altra parte, le matrici singolari sono anche chiamate matrici non regolari, perché hanno il significato esattamente opposto di matrice regolare .

Esempi di matrici singolari

Una volta vista la spiegazione della matrice singolare o degenere, vediamo alcuni esempi di matrici singolari a più dimensioni:

Esempio di matrice singolare 2×2

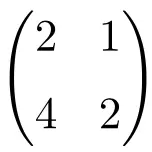
esempio di matrice singolare o degenere di dimensione 2x2

Possiamo facilmente verificare che si tratta di una matrice singolare calcolandone il determinante:

$\displaystyle\begin{vmatrix} 2&1 \\[1.1ex] 4 & 2\end{vmatrix}\bm{=0}$

Il determinante della matrice di ordine 2 è uguale a 0, quindi è una matrice singolare.

Esempio di matrice singolare 3×3

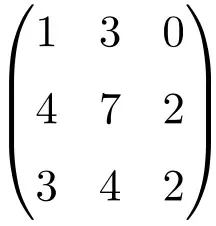
esempio di matrice singolare o degenere di dimensione 3x3

Dobbiamo risolvere il determinante della matrice per verificare che si tratti di una matrice non invertibile:

$\displaystyle\begin{vmatrix} 1&3&0\\[1.1ex] 4&7&2\\[1.1ex] 3&4&2\end{vmatrix}\bm{=0}$

Il determinante della matrice di ordine 3 dà 0, è quindi una matrice singolare.

Esempio di matrice singolare 4 × 4

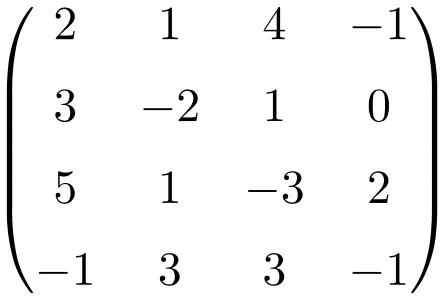
esempio di matrice singolare o degenere di dimensione 4x4

Facendo il determinante della matrice mostriamo che si tratta di una matrice singolare:

$\displaystyle\begin{vmatrix} 2&1&4&-1\\[1.1ex] 3&-2&1&0\\[1.1ex] 5&1&-3&2\\[1.1ex] -1&3&3&-1\end{vmatrix}\bm{=0}$

Il determinante della matrice di ordine 4 è zero, quindi la sua matrice inversa non esiste.

Attenzione: Se hai dubbi sui calcoli dei determinanti puoi consultare la pagina come calcolare un determinante .

Proprietà delle matrici singolari

Le caratteristiche di questo tipo di matrici sono le seguenti:

Almeno due colonne o due righe di una matrice singolare sono combinazioni lineari e sono lineari quindi dipendenti.

Qualsiasi matrice contenente una riga o una colonna riempita di zeri è una matrice singolare.

Il rango di una matrice singolare o degenere è inferiore alla sua dimensione.

Il prodotto matriciale di una matrice singolare moltiplicato per qualsiasi altra matrice dà un’altra matrice singolare. Questa condizione può essere dedotta dalle proprietà dei determinanti:

$\text{det}(AB) = \text{det}(A) \cdot \text{det}(B)=0 \cdot \text{det}(B) = 0$

Allo stesso modo, la potenza di una matrice singolare è uguale a quella di un’altra matrice singolare, indipendentemente dalla potenza a cui è elevata.

La trasposizione di una matrice singolare dà origine ad un’altra matrice singolare, poiché il determinante di una matrice trasposta (o trasposta) è equivalente al determinante della matrice non trasposta:

$\text{det}(A^t) = \text{det}(A)=0$

Moltiplicando una matrice singolare per uno scalare non cambia il suo status di matrice degenere.

Anche l’ aggiunto di una matrice singolare è singolare.

Le matrici triangolari e le matrici diagonali sono matrici degeneri se almeno un elemento della loro diagonale principale è zero.

Ovviamente la matrice zero è una matrice singolare.

Allo stesso modo, anche una matrice nilpotente è una matrice singolare.

Un sistema di equazioni lineari associato ad una matrice singolare non ha soluzioni o ha infinite soluzioni.

Infine, una matrice quadrata è singolare se e solo se ha almeno un autovalore (o autovalore) pari a 0.