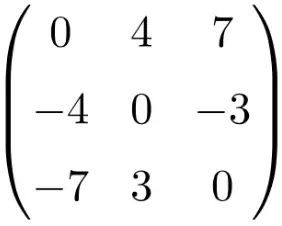In questa pagina spieghiamo cos’è una matrice quadrata e troverai esempi di matrici quadrate. Inoltre, vedrai quali proprietà hanno le matrici quadrate, le operazioni che si possono fare con esse e i diversi tipi che esistono.
Cos’è una matrice quadrata?
Una matrice quadrata è a matrice che ha lo stesso numero di righe che di colonne.
Esempi di matrici quadrate
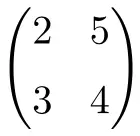
matrice quadrata di ordine 2
matrice quadrata di ordine 3
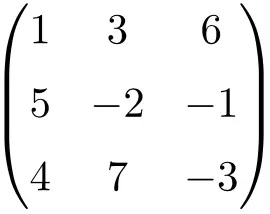
matrice quadrata di ordine 4
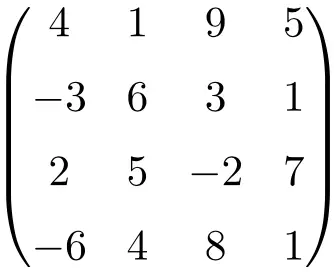
Come puoi vedere, le matrici quadrate vengono solitamente denominate in base al loro ordine, ovvero una matrice quadrata di ordine 2 significa che è una matrice di dimensione 2×2 (2 righe e 2 colonne), oppure parliamo di una matrice quadrata di ordine 3 che indica che è di dimensione 3×3 (3 righe e 3 colonne).
Diagonali di una matrice quadrata
Le diagonali delle matrici quadrate hanno nomi particolari, c’è la diagonale principale e la diagonale secondaria:
- La diagonale principale di una matrice quadrata è costituita dagli elementi che vanno dall’angolo in alto a sinistra all’angolo in basso a destra:

- La diagonale secondaria di una matrice quadrata corrisponde agli elementi che vanno dall’angolo in basso a sinistra all’angolo in alto a destra:

Proprietà di una matrice quadrata
Le matrici quadrate sono ampiamente utilizzate nell’algebra lineare, motivo per cui sono così importanti. Vediamo quindi quali sono le caratteristiche che rendono questa classe di matrici così rilevante:
- Qualsiasi matrice quadrata può essere scomposta nella somma di una matrice simmetrica e di una matrice antisimmetrica .
- Se due matrici quadrate sono dello stesso ordine, possono essere sommate o sottratte l’una dall’altra:
![Rendered by QuickLaTeX.com \begin{pmatrix}5&2&-3\\[1.1ex] 1&9&7\\[1.1ex] 4&1&-2\end{pmatrix} + \begin{pmatrix}2&3&0\\[1.1ex] 8&6&-4\\[1.1ex] 1&3&-1\end{pmatrix} = \begin{pmatrix}7&5&-3\\[1.1ex] 9&15&3\\[1.1ex] 5&4&-3\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3cec5286f22acdb6c84e876264157a89_l3.png)
- Due matrici quadrate possono essere moltiplicate in entrambe le direzioni possibili. Tuttavia, il prodotto di matrici quadrate non è commutativo, cioè il risultato della moltiplicazione cambierà a seconda del lato per cui viene moltiplicato. Notare nell’esempio seguente come il risultato dipende dalle posizioni delle matrici:
![Rendered by QuickLaTeX.com \begin{pmatrix}3&-1\\[1.1ex] 4&0 \end{pmatrix} \cdot \begin{pmatrix}5&2\\[1.1ex] 3&1 \end{pmatrix} = \begin{pmatrix}12&5\\[1.1ex] 20&8\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6bdc76d296851b4ea7aa79124a026a01_l3.png)
![Rendered by QuickLaTeX.com \begin{pmatrix}5&2\\[1.1ex] 3&1 \end{pmatrix} \cdot \begin{pmatrix}3&-1\\[1.1ex] 4&0 \end{pmatrix}= \begin{pmatrix}23&-5\\[1.1ex] 13&-3\end{pmatrix}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6405df17f38fb056fe7e5ab9e218f960_l3.png)
- Le matrici quadrate sono le uniche che possono calcolare il determinante. Pertanto, un determinante può essere risolto solo se è una matrice quadrata. Ad esempio, per trovare il determinante di una matrice quadrata 3×3, è necessario applicare la regola di Sarrus:
![Rendered by QuickLaTeX.com \displaystyle\begin{aligned} \begin{vmatrix} 1 & 3 & 1 \\[1.1ex] 0 & 2 & 4 \\[1.1ex] -1 & 5 & 1 \end{vmatrix} & = \\ & = 1 \cdot 2 \cdot 1 + 3 \cdot 4 \cdot (-1) + 0 \cdot 5 \cdot 1 \ - \\[1.1ex] & \phantom{=} - (-1) \cdot 2 \cdot 1 - 5\cdot 4 \cdot 1 - 0 \cdot 3 \cdot 1 \\[2.5ex] & =2 -12 +0 +2-20-0 \\[2.5ex] & = -28 \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-b6da09d0b791b047beec0aa2f3da1825_l3.png)
Ricordiamo inoltre che se il determinante della matrice è diverso da 0 significa che si tratta di una matrice regolare , cioè è invertibile. D’altra parte, se il determinante è zero, è una matrice singolare (che non ha inversa).
- Infine, le matrici quadrate possono essere diagonalizzate . Si può quindi effettuare un cambio di base per calcolare gli autovalori (o autovalori) e gli autovettori (o autovettori) di una matrice quadrata.
Operazioni con matrici quadrate
Come abbiamo visto, il determinante di una matrice può essere calcolato solo se la matrice è quadrata. Allo stesso modo, ci sono anche alcune operazioni che possono essere eseguite solo se la matrice è di dimensione quadrata:
traccia di una matrice
La traccia di una matrice è la somma degli elementi che formano la diagonale principale di una matrice quadrata.
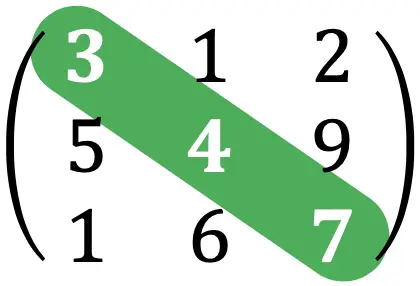
Ad esempio, la traccia della matrice dell’esercizio precedente sarebbe:
![]()
Tipi di trafile quadrate
Quindi hai i tipi più importanti di matrici quadrate esistenti. Clicca sul tipo di fustella per scoprire cosa ha di speciale.
Come puoi vedere, esistono molti tipi di matrici quadrate e ciascuna ha il proprio nome per un motivo diverso.