Matrice regolare - Mathority

In questa pagina vedrai cos’è una matrice normale e alcuni esempi di matrici normali. Inoltre troverai le proprietà di questo tipo di matrici e gli esercizi risolti passo dopo passo.

Cos’è una matrice normale?

La definizione di array normale è:

Una matrice normale è una matrice complessa che moltiplicata per la sua matrice di trasposizione coniugata è uguale al prodotto della trasposizione coniugata da sola.

$A\cdot A^*=A^*\cdot A$

Oro

$A^*$

è la matrice di trasposizione coniugata di

$A$

Se però si tratta di matrici di numeri reali , la condizione precedente equivale a dire che una matrice commuta con la sua trasposta, cioè:

$A\cdot A^t=A^t\cdot A$

Perché, ovviamente, la matrice di trasposizione coniugata di una matrice reale è semplicemente la matrice di trasposizione (o trasposizione).

Esempi di matrici normali

Esempio con numeri complessi

La seguente matrice quadrata complessa di dimensione 2×2 è normale:

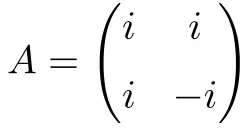
esempio di matrice normale con numeri complessi di dimensione 2x2

La dimostrazione della sua normalità è allegata di seguito:

$\displaystyle A\cdot A^* = \begin{pmatrix} i & i \\[1.1ex] i & -i \end{pmatrix} \cdot \begin{pmatrix} -i & -i \\[1.1ex] -i & i \end{pmatrix} =\begin{pmatrix} 2 & 0 \\[1.1ex] 0 & 2 \end{pmatrix}$

$\displaystyle A^*\cdot A = \begin{pmatrix} -i & -i \\[1.1ex] -i & i \end{pmatrix}\cdot \begin{pmatrix} i & i \\[1.1ex] i & -i \end{pmatrix} = \begin{pmatrix} 2 & 0 \\[1.1ex] 0 & 2 \end{pmatrix}$

Esempio con numeri reali

Anche la seguente matrice quadrata con numeri reali di ordine 2 è normale:

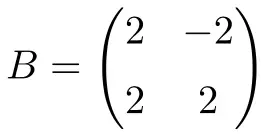
esempio di matrice normale con numeri reali di dimensione 2x2

In questo caso, poiché ha solo numeri reali, per dimostrare che è normale è sufficiente verificare che la matrice sia commutabile con la sua trasposta:

$\displaystyle B\cdot B^t = \begin{pmatrix} 2 & -2 \\[1.1ex] 2 & 2 \end{pmatrix} \cdot \begin{pmatrix} 2 & 2 \\[1.1ex] -2 & 2 \end{pmatrix} =\begin{pmatrix} 8 & 0 \\[1.1ex] 0 & 8 \end{pmatrix}$

$\displaystyle B^t\cdot B =\begin{pmatrix} 2 & 2 \\[1.1ex] -2 & 2 \end{pmatrix}\cdot \begin{pmatrix} 2 & -2 \\[1.1ex] 2 & 2 \end{pmatrix} =\begin{pmatrix} 8 & 0 \\[1.1ex] 0 & 8 \end{pmatrix}$

Proprietà delle matrici normali

Le matrici normali hanno le seguenti caratteristiche:

Tutte le matrici normali sono matrici diagonalizzabili.

Ogni matrice unitaria è anche una matrice normale.

Allo stesso modo, una matrice hermitiana è una matrice normale.

Allo stesso modo, una matrice antihermitiana è una matrice normale.

Se A è una matrice normale, gli autovalori (o autovalori) della matrice trasposta coniugata A* sono gli autovalori coniugati di A.

$\displaystyle A=\begin{pmatrix}2i&-1+i\\[1.1ex] 1+i&i\end{pmatrix} \longrightarrow \ \lambda_{A,1} = 0 \ ; \ \lambda_{A,2} = +3i$

$\displaystyle A^*=\begin{pmatrix}-2i&1-i\\[1.1ex] -1-i&-i\end{pmatrix} \longrightarrow \ \lambda_{A^*,1} = 0 \ ; \ \lambda_{A^*,2} = -3i$

Nelle matrici normali gli autovettori (o autovettori) associati ai diversi autovalori sono ortogonali.

Se una matrice è composta solo da numeri reali ed è simmetrica , è allo stesso tempo una matrice normale.

Allo stesso modo, anche una matrice reale antisimmetrica è una matrice normale.

Infine, anche qualsiasi matrice ortogonale formata da numeri reali è una matrice normale.

Esercizi risolti per matrici normali

Esercizio 1

Verificare che la seguente matrice complessa di dimensione 2 × 2 sia normale:

$\displaystyle A=\begin{pmatrix}1&2+3i\\[1.1ex] 2+3i&1\end{pmatrix}$

vedi soluzione

Per dimostrare che la matrice è normale dobbiamo prima calcolare la sua trasposta coniugata:

$\displaystyle A^*=\begin{pmatrix}1&2-3i\\[1.1ex] 2-3i&1\end{pmatrix}$

E ora facciamo la verifica moltiplicando la matrice A per la matrice A* in entrambe le possibili direzioni:

$\displaystyle A\cdot A^* = \begin{pmatrix}1&2+3i\\[1.1ex] 2+3i&1\end{pmatrix}\cdot \begin{pmatrix}1&2-3i\\[1.1ex] 2-3i&1\end{pmatrix} = \begin{pmatrix}14&4\\[1.1ex] 4&14\end{pmatrix}$

$\displaystyle A^*\cdot A =\begin{pmatrix}1&2-3i\\[1.1ex] 2-3i&1\end{pmatrix}\cdot \begin{pmatrix}1&2+3i\\[1.1ex] 2+3i&1\end{pmatrix} = \begin{pmatrix}14&4\\[1.1ex] 4&14\end{pmatrix}$

Il risultato di entrambe le moltiplicazioni è lo stesso, quindi la matrice A è normale.

Esercizio 2

Mostra che la seguente matrice reale di dimensione 2 × 2 è normale:

$\displaystyle A=\begin{pmatrix}3&5\\[1.1ex] -5&3\end{pmatrix}$

vedi soluzione

Poiché in questo caso abbiamo a che fare con un ambiente di soli numeri reali, è sufficiente verificare che il prodotto matriciale tra la matrice A e la sua trasposta dà lo stesso risultato qualunque sia la direzione della moltiplicazione:

$\displaystyle A\cdot A^t = \begin{pmatrix}3&5\\[1.1ex] -5&3\end{pmatrix}\cdot \begin{pmatrix}3&-5\\[1.1ex] 5&3\end{pmatrix} = \begin{pmatrix}34&0\\[1.1ex] 0&34\end{pmatrix}$

$\displaystyle A^t\cdot A = \begin{pmatrix}3&-5\\[1.1ex] 5&3\end{pmatrix}\cdot \begin{pmatrix}3&5\\[1.1ex] -5&3\end{pmatrix} = \begin{pmatrix}34&0\\[1.1ex] 0&34\end{pmatrix}$

Il risultato di entrambi i prodotti è lo stesso, quindi la matrice A è normale.

Esercizio 3

Determina se la seguente matrice di numeri complessi di ordine 2 è normale:

$\displaystyle A=\begin{pmatrix}4i&-1+i\\[1.1ex] 1-i&4i\end{pmatrix}$

vedi soluzione

Per verificare che la matrice sia normale, dobbiamo prima calcolare la sua trasposta coniugata:

$\displaystyle A^*=\begin{pmatrix}-4i&1+i\\[1.1ex] -1-i&-4i\end{pmatrix}$

E ora controlliamo se la matrice A e la sua trasposizione coniugata sono commutabili:

$\displaystyle A\cdot A^* = \begin{pmatrix}4i&-1+i\\[1.1ex] 1-i&4i\end{pmatrix}\cdot \begin{pmatrix}-4i&1+i\\[1.1ex] -1-i&-4i\end{pmatrix} = \begin{pmatrix}18&8i\\[1.1ex] -8i&18\end{pmatrix}$

$\displaystyle A^*\cdot A =\begin{pmatrix}-4i&1+i\\[1.1ex] -1-i&-4i\end{pmatrix}\cdot \begin{pmatrix}4i&-1+i\\[1.1ex] 1-i&4i\end{pmatrix} = \begin{pmatrix}18&8i\\[1.1ex] -8i&18\end{pmatrix}$

Il risultato di entrambe le moltiplicazioni è lo stesso, quindi la matrice A è normale.

Esercizio 4

Verificare che la seguente matrice reale di dimensione 3×3 è normale:

$\displaystyle A=\begin{pmatrix} -1&1&0\\[1.1ex] 0&-1&1\\[1.1ex] 1&0&-1\end{pmatrix}$

vedi soluzione

Essendo la matrice interamente composta da elementi reali, è sufficiente verificare che il prodotto matriciale tra la matrice A e la sua trasposta è indipendente dalla direzione della moltiplicazione:

$\displaystyle A\cdot A^t = \begin{pmatrix} -1&1&0\\[1.1ex] 0&-1&1\\[1.1ex] 1&0&-1\end{pmatrix} \cdot\begin{pmatrix}-1&0&1\\[1.1ex] 1&-1&0\\[1.1ex] 0&1&-1\end{pmatrix}=\begin{pmatrix}2&-1&-1\\[1.1ex] -1&2&-1\\[1.1ex] -1&-1&2\end{pmatrix}$

$\displaystyle A^t\cdot A =\begin{pmatrix}-1&0&1\\[1.1ex] 1&-1&0\\[1.1ex] 0&1&-1\end{pmatrix}\cdot \begin{pmatrix} -1&1&0\\[1.1ex] 0&-1&1\\[1.1ex] 1&0&-1\end{pmatrix}=\begin{pmatrix}2&-1&-1\\[1.1ex] -1&2&-1\\[1.1ex] -1&-1&2\end{pmatrix}$

Il risultato di entrambi i prodotti è lo stesso, quindi la matrice A è normale.

Esercizio 5

Determina se la seguente matrice complessa di ordine 3×3 è normale:

$\displaystyle A=\begin{pmatrix}4&3-2i & 5i \\[1.1ex] 3+2i & 0 & -1-3i \\[1.1ex] -5i & -1+3i & 1\end{pmatrix}$

vedi soluzione

Innanzitutto, calcoliamo la trasposta coniugata della matrice:

$\displaystyle A^*=\begin{pmatrix}4&3-2i & 5i \\[1.1ex] 3+2i & 0 & -1-3i \\[1.1ex] -5i & -1+3i & 1\end{pmatrix}$

Ora dobbiamo fare le moltiplicazioni di matrice tra la matrice A e il suo coniugato trasposto in entrambe le possibili direzioni. Tuttavia, la matrice trasposta coniugata di A è uguale alla matrice A stessa, quindi è una matrice hermitiana. E quindi, dalle proprietà delle matrici normali ne consegue che A è una matrice normale , perché ogni matrice Hermitiana è una matrice normale.

Cos’è una matrice normale?

Esempi di matrici normali

Esempio con numeri complessi

Esempio con numeri reali

Proprietà delle matrici normali

Esercizi risolti per matrici normali

Esercizio 1

Esercizio 2

Esercizio 3

Esercizio 4

Esercizio 5

Lascia un commento Annulla risposta