Jacobiana e matrice Jacobiana

In questa pagina troverai cos’è la matrice Jacobiana e come calcolarla utilizzando un esempio. Inoltre, hai diversi esercizi risolti sulle matrici Jacobiane in modo che tu possa esercitarti. Vedrai anche perché il determinante della matrice Jacobiana, lo Jacobiano, è così importante. Infine, spieghiamo le relazioni che questa matrice mantiene con le altre operazioni e le applicazioni che ha.

Cos’è la matrice Jacobiana?

La definizione della matrice Jacobiana è la seguente:

La matrice Jacobiana è una matrice formata dalle derivate parziali del primo ordine di una funzione.

La formula per la matrice Jacobiana è quindi la seguente:

Pertanto, le matrici Jacobiane avranno sempre tante righe quante sono le funzioni scalari

$(f_1,f_2,\ldots ,f_m)$

hanno la funzione e il numero di colonne corrisponderà al numero di variabili

$(x_1, x_2, \ldots , x_n).$

D’altra parte, questa matrice è anche conosciuta come mappa differenziale Jacobiana o mappa lineare Jacobiana . Infatti a volte viene scritto anche con la lettera D al posto della lettera J:

$\displaystyle J_f = D_f$

Per curiosità, la matrice Jacobiana prende il nome da Carl Gustav Jacobi, un importante matematico e professore del XIX secolo che diede importanti contributi al mondo della matematica, in particolare nel campo dell’algebra lineare.

Esempio di calcolo della matrice Jacobiana

Una volta compreso il concetto di matrice Jacobiana, vedremo passo dopo passo come viene calcolata utilizzando un esempio:

Determina la matrice Jacobiana al punto (1,2) della seguente funzione:

$\displaystyle f(x,y)= (x^4 +3y^2x \ , \ 5y^2-2xy+1)$

La prima cosa che dobbiamo fare è calcolare tutte le derivate parziali del primo ordine della funzione:

$\displaystyle \cfrac{\partial f_1}{\partial x} = 4x^3+3y^2$

$\displaystyle \cfrac{\partial f_1}{\partial y} = 6yx$

$\displaystyle \cfrac{\partial f_2}{\partial x} = -2y$

$\displaystyle \cfrac{\partial f_2}{\partial y} = 10y-2x$

Ora applichiamo la formula della matrice Jacobiana. In questo caso la funzione ha due variabili e due funzioni scalari, quindi la matrice Jacobiana sarà una matrice quadrata di dimensione 2×2:

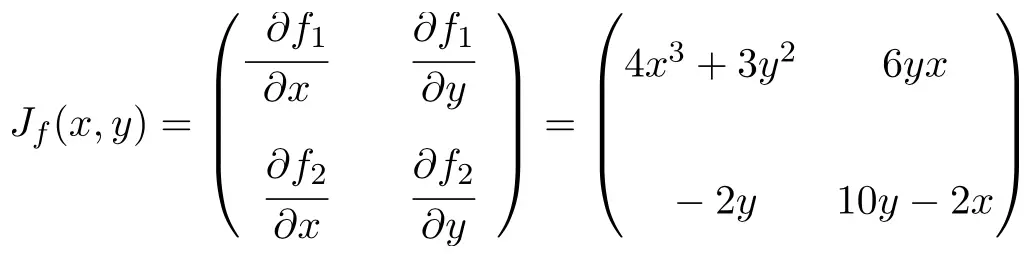
Una volta ottenuta l’espressione per la matrice Jacobiana, la valutiamo al punto (1,2):

$\displaystyle J_f(1,2)=\begin{pmatrix} 4\cdot 1^3+3\cdot 2^2 & 6\cdot 2 \cdot 1 \\[3ex] -2\cdot 2 & 10\cdot 2-2 \cdot 1 \end{pmatrix}$

E, infine, effettuiamo le operazioni e otteniamo la soluzione:

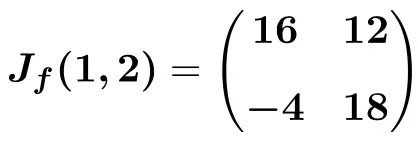
esempio di calcolo della matrice Jacobiana

Una volta che hai visto come trovare la matrice Jacobiana di una funzione, ti lasciamo diversi esercizi risolti passo passo in modo che tu possa esercitarti.

Problemi risolti di matrici Jacobiane

Esercizio 1

Trova la matrice Jacobiana nel punto (0,-2) della seguente funzione vettoriale in 2 variabili:

$\displaystyle f(x,y)= (e^{xy}+y \ , \ y^2x)$

vedi soluzione

La funzione ha due variabili e due funzioni scalari, quindi la matrice Jacobiana sarà una matrice quadrata di dimensione 2×2:

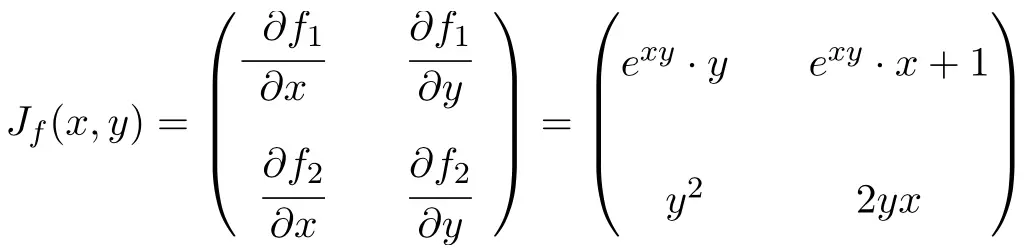
esercizio sulla matrice Jacobiana risolto

Una volta calcolata l’espressione per la matrice Jacobiana, la valutiamo nel punto (0,-2):

$\displaystyle J_f(0,-2)=\begin{pmatrix}e^{0\cdot (-2)}\cdot (-2)\phantom{5} & \phantom{5}e^{0\cdot (-2)} \cdot 0 +1 \\[4ex](-2)^2 & 2\cdot (-2) \cdot 0 \end{pmatrix}$

E, infine, eseguiamo le operazioni e otteniamo il risultato:

$\displaystyle \bm{J_f(0,-2)}=\begin{pmatrix} \bm{-2} & \bm{1} \\[1.5ex] \bm{4} & \bm{0} \end{pmatrix}$

Esercizio 2

Calcola la matrice Jacobiana nel punto (2,-1) della seguente funzione con 2 variabili:

$\displaystyle f(x,y)= (x^3y^2 - 5x^2y^2 \ , \ y^6-3y^3x+7)$

vedi soluzione

In questo caso la funzione ha due variabili e due funzioni scalari, quindi la matrice Jacobiana sarà una matrice quadrata di ordine 2:

$\displaystyle J_f(x,y)=\begin{pmatrix}\cfrac{\phantom{5}\partial f_1}{\partial x}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial y}\phantom{5} \\[3ex] \cfrac{\partial f_2}{\partial x} & \cfrac{\partial f_2}{\partial y}\end{pmatrix} = \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}}3x^2y^2-10xy^2& 2x^3y-10x^2y \\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} -3y^3 & 6y^5-9y^2x \end{pmatrix}$

Una volta trovata l’espressione per la matrice Jacobiana, la valutiamo al punto (2,-1):

$\displaystyle J_f(2,-1)=\begin{pmatrix} 3\cdot 2^2\cdot (-1)^2-10\cdot 2 \cdot (-1)^2\phantom{5} & \phantom{5}2\cdot 2^3\cdot (-1)-10\cdot 2^2\cdot (-1) \\[4ex] -3(-1)^3 & 6\cdot (-1)^5-9\cdot (-1)^2\cdot 2 \end{pmatrix}$

E, infine, eseguiamo le operazioni e otteniamo il risultato:

$\displaystyle \bm{J_f(1,2)}=\begin{pmatrix} \bm{-8} & \bm{24} \\[1.5ex] \bm{3} & \bm{-24} \end{pmatrix}$

Esercizio 3

Determina la matrice Jacobiana nel punto (2,-2,2) della seguente funzione con 3 variabili:

$\displaystyle f(x,y,z)= \left(z\tan (x^2-y^2) \ , \ xy\ln \left( \frac{z}{2} \right)\right)$

vedi soluzione

In questo caso la funzione ha tre variabili e due funzioni scalari, quindi la matrice Jacobiana sarà una matrice rettangolare di dimensione 2×3:

$\displaystyle J_f(x,y,z)= \begin{pmatrix}\cfrac{\phantom{5}\partial f_1}{\partial x}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial y}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial z}\phantom{5} \\[3ex] \cfrac{\partial f_2}{\partial x} & \cfrac{\partial f_2}{\partial y} &\cfrac{\partial f_2}{\partial z}\end{pmatrix}$

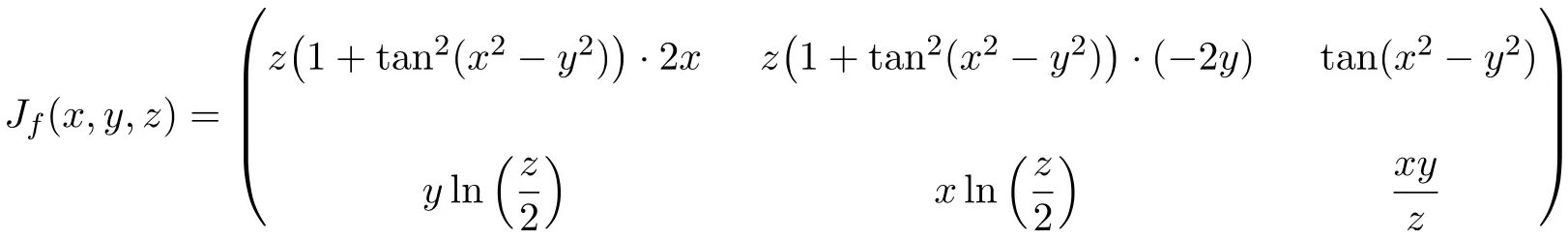
Matrice Jacobiana risolto esercizio di 3 variabili

Una volta ottenuta l’espressione per la matrice Jacobiana, la valutiamo al punto (2,-2,2):

$\displaystyle J_f(2,-2,2)= \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}}2\bigl(1+\tan^2 (2^2-(-2)^2)\bigr) \cdot 2\cdot 2 & 2\bigl(1+\tan^2 (2^2-(-2)^2)\bigr) \cdot (-2\cdot (-2)) & \tan (2^2-(-2)^2)\\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} \displaystyle -2\ln \left( \frac{2}{2} \right) & \displaystyle 2\ln \left( \frac{2}{2} \right) &\displaystyle \frac{2\cdot (-2)}{2} \right)\end{pmatrix}$

Effettuiamo i calcoli:

$\displaystyle J_f(2,-2,2)= \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}}2\bigl(1+\tan^2 (0)\bigr) \cdot 4 \phantom{5} & 2\bigl(1+\tan^2 (0)\bigr) \cdot 4 & \phantom{5}\tan (0)\\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} -2\cdot 0 & 2\cdot 0 &-2 \right)\end{pmatrix}$

E continuiamo a operare finché non sarà più possibile semplificarlo:

$\displaystyle \bm{J_f(2,-2,2)=} \begin{pmatrix}\bm{8} & \bm{8} & \bm{0} \\[2ex] \bm{0} & \bm{0} &\bm{-2} \right)\end{pmatrix}$

Esercizio 4

Determina la matrice Jacobiana nel punto

$(\pi, \pi)$

della seguente funzione multivariabile:

$\displaystyle f(x,y)= \left( \frac{\cos (x-y)}{x} \ , \ e^{x^2-y^2} \ , \ x^3\sin (2y) \right)$

vedi soluzione

In questo caso la funzione ha due variabili e tre funzioni scalari, quindi la matrice Jacobiana sarà una matrice rettangolare di dimensione 3×2:

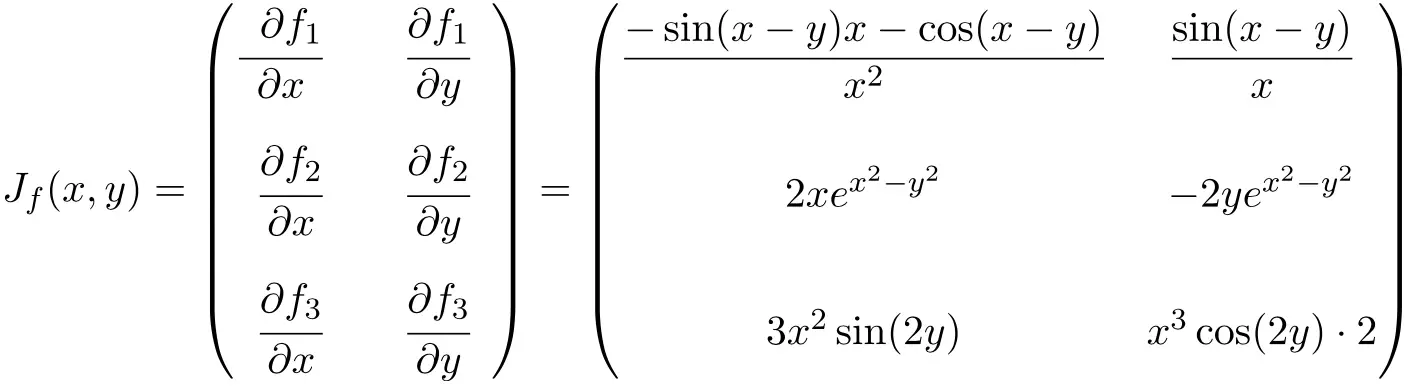
esercizio risolto passo passo della matrice Jacobiana

Una volta ottenuta l’espressione per la matrice Jacobiana, la valutiamo al punto

$(\pi, \pi):$

$\displaystyle J_f(\pi,\pi)= \begin{pmatrix} \displaystyle \vphantom{\cfrac{\partial f_3}{\partial y}}\frac{-\sin(\pi-\pi)\pi-\cos(\pi-\pi)}{\pi^2} & \displaystyle\frac{\sin (\pi- \pi)}{\pi} \\[3ex] \vphantom{\cfrac{\partial f_3}{\partial y}}2\pi e^{\pi^2-\pi^2} & -2\pi e^{\pi^2-\pi^2} \\[3ex] \vphantom{\cfrac{\partial f_3}{\partial y}} 3\pi^2\sin(2\pi) & \pi^3 \cos(2\pi)\cdot 2 \end{pmatrix}$

Effettuiamo le operazioni:

$\displaystyle J_f(\pi,\pi)= \begin{pmatrix} \displaystyle \vphantom{\cfrac{\partial f_3}{\partial y}}\displaystyle\frac{-0-1}{\pi^2} & \displaystyle\frac{0}{\pi} \\[3ex] \vphantom{\cfrac{\partial f_3}{\partial y}}2\pi e^{0} & -2\pi e^{0} \\[3ex] \vphantom{\cfrac{\partial f_3}{\partial y}} 3\pi^2\cdot 0 & \pi^3 \cdot 1 \cdot 2 \end{pmatrix}$

Quindi la matrice Jacobiana della funzione vettoriale nel punto considerato vale:

$\displaystyle \bm{J_f(\pi,\pi)=} \begin{pmatrix}\displaystyle -\frac{\bm{1}}{\bm{\pi^2}} & \bm{0} \\[3ex] \bm{2\pi} & \bm{-2\pi}\\[3ex]\bm{0} & \bm{2\pi^3} \right)\end{pmatrix}$

Esercizio 5

Calcola la matrice Jacobiana nel punto

$(3,0,\pi)$

della seguente funzione con 3 variabili:

$\displaystyle f(x,y,z)= \left(xe^{2y}\cos(-z) \ , \ (y-2)^3\cdot \sin\left(\frac{z}{2}\right) \ , \ e^{2y}\cdot \ln\left(\frac{x}{3}\right) \right)$

vedi soluzione

In questo caso la funzione è di tre variabili e tre funzioni scalari, quindi la matrice Jacobiana sarà una matrice quadrata di dimensione 3×3:

$\displaystyle J_f(x,y,z)=\begin{pmatrix}\phantom{5}\cfrac{\partial f_1}{\partial x}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial y}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial z}\phantom{5} \\[3ex] \cfrac{\partial f_2}{\partial x} & \cfrac{\partial f_2}{\partial y} & \cfrac{\partial f_2}{\partial z} \\[3ex] \cfrac{\partial f_3}{\partial x} & \cfrac{\partial f_3}{\partial y} & \cfrac{\partial f_3}{\partial z}\end{pmatrix}$

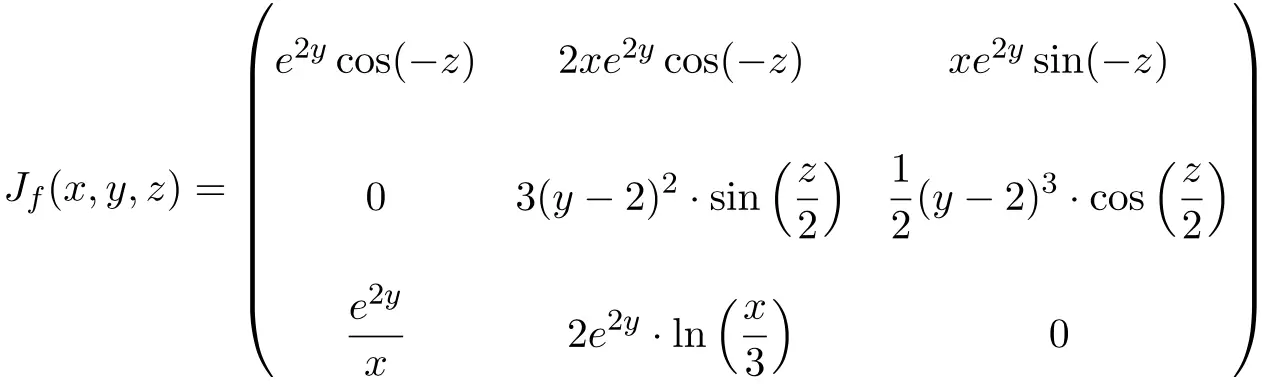
Esercizio risolto di matrice Jacobiana 3x3 con 3 variabili

Una volta trovata la matrice Jacobiana, la valutiamo sul punto

$(3,0,\pi):$

$\displaystyle J_f(3,0,\pi)= \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}} e^{2\cdot 0}\cos(-\pi) & 2\cdot 3e^{2\cdot 0}\cos(-\pi) & 3e^{2\cdot 0}\sin(-\pi) \\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} 0 & \displaystyle 3(0-2)^2\cdot \sin\left(\frac{\pi}{2}\right) & \displaystyle\frac{1}{2}(0-2)^3\cdot \cos\left(\frac{\pi}{2}\right)\\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}}\displaystyle\frac{e^{2\cdot 0}}{3} &\displaystyle 2e^{2\cdot 0}\cdot \ln\left(\frac{3}{3}\right) & 0\end{pmatrix}$

Calcoliamo le operazioni:

$\displaystyle J_f(3,0,\pi)= \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}} 1\cdot (-1) & 6\cdot 1\cdot (-1) & 3\cdot 1 \cdot 0 \\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}} 0 & \displaystyle 3\cdot 4 \cdot 1 & \displaystyle\frac{1}{2}\cdot (-8)\cdot 0\\[3ex] \vphantom{\cfrac{\partial f_2}{\partial x}}\displaystyle\frac{1}{3} &\displaystyle 2\cdot 1\cdot 0 & 0\end{pmatrix}$

E il risultato della matrice Jacobiana in quel punto è:

$\displaystyle \bm{J_f(3,0,\pi)=} \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}} \bm{-1} & \bm{-6} & \phantom{-}\bm{0} \\[2ex] \bm{0} & \bm{12} & \displaystyle \bm{0} \\[2ex] \displaystyle \frac{\bm{1}}{\bm{3}} &\bm{0}& \bm{0}\end{pmatrix}$

Determinante della matrice Jacobiana: lo Jacobiano

Il determinante della matrice Jacobiana è chiamato determinante Jacobiano o Jacobiano. Bisogna tenere conto che lo Jacobiano si può calcolare solo se la funzione ha lo stesso numero di variabili delle funzioni scalari, perché allora la matrice Jacobiana avrà lo stesso numero di righe e colonne e, quindi, sarà un quadrato matrice. .

Esempio Jacobiano

Vediamo un esempio di calcolo del determinante Jacobiano di una funzione con due variabili:

$\displaystyle f(x,y)= (x^2-y^2 \ , \ 2xy)$

Per prima cosa calcoliamo la matrice Jacobiana della funzione:

$\displaystyle J_f(x,y)=\begin{pmatrix}\cfrac{\phantom{5}\partial f_1}{\partial x}\phantom{5} & \phantom{5}\cfrac{\partial f_1}{\partial y}\phantom{5} \\[3ex] \cfrac{\partial f_2}{\partial x} & \cfrac{\partial f_2}{\partial y}\end{pmatrix} = \begin{pmatrix} \vphantom{\cfrac{\partial f_2}{\partial x}}2x \phantom{5}& -2y \\[2ex] \vphantom{\cfrac{\partial f_2}{\partial x}} 2y & 2x \end{pmatrix}$

E ora risolviamo il determinante della matrice 2×2:

$\displaystyle \text{det}\bigl(J_f(x,y)\bigr) =\begin{vmatrix} 2x&-2y \\[2ex] 2y & 2x \end{vmatrix} = \bm{4x^2+4y^2}$

Lo Jacobiano e l’invertibilità di una funzione

Ora che hai visto il concetto di Jacobiano, probabilmente hai pensato… beh, qual è il punto?

Bene, l’uso principale dello Jacobiano è determinare se una funzione può essere invertita. Il teorema della funzione inversa dice che se il determinante della matrice Jacobiana (lo Jacobiano) è diverso da 0, ciò significa che questa funzione è invertibile.

$\displaystyle \text{det}\bigl(J_f\bigr) \neq 0 \ \longrightarrow \ \exists \ f^{-1}$

Va notato che questa condizione è necessaria ma non sufficiente, cioè se il determinante è diverso da zero possiamo affermare che la matrice può essere invertita, invece se il determinante è 0 non possiamo sapere se il la funzione ha un inverso o n.

Ad esempio, nell’esempio visto in precedenza di come trovare lo Jacobiano di una funzione, il determinante dà

$4x^2+4y^2$

. In questo caso possiamo affermare che la funzione può sempre essere invertita tranne che nel punto (0,0), poiché questo punto è l’unico in cui il determinante Jacobiano è uguale a zero e, quindi, non sappiamo se la funzione inversa esiste in questo punto.

Relazione della matrice Jacobiana con altre operazioni

La matrice Jacobiana è legata al gradiente e alla matrice Hessiana di una funzione:

Pendenza

Se la funzione è una funzione scalare, la matrice Jacobiana sarà una matrice di righe che sarà equivalente al gradiente :

$\displaystyle f: \mathbb{R}^n \to \mathbb{R}$

$\displaystyle J_f = \nabla f = \begin{pmatrix}\phantom{5} \cfrac{\partial f}{\partial x_1} \phantom{5}& \cfrac{\partial f}{\partial x_2}& \dots & \cfrac{\partial f}{\partial x_n}\phantom{5} \end{pmatrix}$

Matrice dell’Assia

La matrice Jacobiana del gradiente di una funzione è uguale alla matrice Hessiana :

$\displaystyle H_f = J(\nabla f)$

L’Hessiana è una matrice molto importante per la derivazione di funzioni con più variabili, perché è formata dalle derivate seconde della funzione. In effetti, si potrebbe dire che la matrice Hessiana è la continuità della matrice Jacobiana. Ma è così importante che abbiamo un’intera pagina che lo spiega in dettaglio. Quindi, se vuoi sapere esattamente cos’è questa matrice e perché è così speciale, puoi fare clic sul collegamento.

Applicazioni della matrice Jacobiana

Oltre all’utilità che abbiamo visto dello Jacobiano, che determina se una funzione è invertibile, la matrice Jacobiana ha altre applicazioni.

La matrice Jacobiana viene utilizzata per calcolare i punti critici di una funzione multivariata, che vengono poi classificati in massimi, minimi o punti di sella attraverso la matrice Hessiana. Per trovare i punti critici, è necessario calcolare la matrice Jacobiana della funzione, impostarla uguale a 0 e risolvere le equazioni risultanti.

$\displaystyle J_f(x)=0$

Inoltre, un’altra applicazione della matrice Jacobiana si trova nell’integrazione di funzioni con più di una variabile, cioè negli integrali doppi, tripli, ecc. Poiché il determinante della matrice Jacobiana consente un cambio di variabile in più integrali secondo la seguente formula:

$\displaystyle x=T(x^*)$

$\displaystyle \int_\Omega f(x)dx=\int_{\Omega^*} f\bigl(T(x^*)\bigr)\cdot \begin{vmatrix} \text{det}\bigl(JT(x^*)\bigr)\end{vmatrix} dx^*$

Dove T è la funzione di cambiamento delle variabili che mette in relazione le variabili originali con quelle nuove.

Infine, la matrice Jacobiana viene utilizzata anche per effettuare un’approssimazione lineare di qualsiasi funzione

$f$

attorno ad un punto

$p$

$\displaystyle f(x) \approx f(p) + J_f(p)(x-p)$

Jacobiana e matrice jacobiana

Cos’è la matrice Jacobiana?

Esempio di calcolo della matrice Jacobiana

Problemi risolti di matrici Jacobiane

Esercizio 1

Esercizio 2

Esercizio 3

Esercizio 4

Esercizio 5

Determinante della matrice Jacobiana: lo Jacobiano

Esempio Jacobiano

Lo Jacobiano e l’invertibilità di una funzione

Relazione della matrice Jacobiana con altre operazioni

Pendenza

Matrice dell’Assia

Applicazioni della matrice Jacobiana

Lascia un commento Annulla risposta