Matrice involutiva

In questa pagina imparerai cos’è una matrice involutiva. Vi mostriamo anche esempi di matrici involutive di dimensioni 2×2, 3×3 e 4×4. E infine troverai la formula per una matrice involutiva.

Cos’è una matrice involutiva?

Il significato della matrice involutiva è il seguente:

Definizione di matrice involutiva : matrice quadrata invertibile la cui matrice inversa è la matrice stessa.

$A^{-1} = A$

Oro

$A$

è una matrice qualsiasi e

$A^{-1}$

rappresenta il suo inverso.

Quindi ovviamente una matrice involutiva è un esempio di matrice regolare o non degenere .

Se non sai cos’è l’inversa di una matrice, puoi vedere qui come calcolare la matrice inversa 3×3 . È importante sapere come invertire una matrice, tuttavia per questo è necessario anche sapere come si calcola l’ aggiunto di una matrice .

Ma torniamo all’argomento: quando una matrice è involutiva, la moltiplicazione della matrice per la matrice stessa dà la matrice identità. Dai un’occhiata alla demo:

Qualsiasi matrice moltiplicata per il suo inverso dà la matrice Identità (o Unità). COSÌ:

$\displaystyle A \cdot A^{-1} = I$

E poiché l’inverso di una matrice involutiva è la matrice stessa:

$\displaystyle A \cdot A = I$

Di conseguenza, una matrice involutiva quadrata dà la matrice identità:

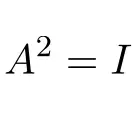
Esempi di matrici involutive

Esempio di matrice involutiva 2×2:

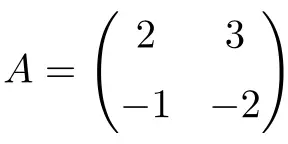
esempio di matrice involutiva di dimensione 2x2

Possiamo verificare che si tratta di una matrice involutiva calcolando la seconda potenza della matrice:

$\displaystyle A^2=\begin{pmatrix} 2 & 3 \\[1.1ex] -1 & -2 \end{pmatrix} \cdot \begin{pmatrix} 2 & 3 \\[1.1ex] -1 & -2 \end{pmatrix}= \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

Poiché la matrice A al quadrato è la matrice identità, la matrice A è una matrice involutiva 2×2.

Esempio di matrice involutiva 3×3:

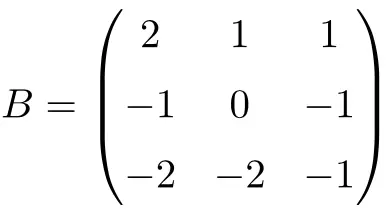
esempio di matrice involutiva di dimensione 3x3

Possiamo verificare che si tratta di una matrice involutiva risolvendo da sola il prodotto della matrice:

$\displaystyle B^2=\begin{pmatrix} 2 & 1 & 1 \\[1.1ex] -1 & 0 & -1 \\[1.1ex] -2 & -2 & -1 \end{pmatrix}\cdot \begin{pmatrix} 2 & 1 & 1 \\[1.1ex] -1 & 0 & -1 \\[1.1ex] -2 & -2 & -1 \end{pmatrix}= \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

Poiché la matrice B al quadrato è la matrice identità, la matrice B è una matrice involutiva 3×3.

Esempio di matrice involutiva 4×4:

La matrice Identità (o Unità), qualunque sia la sua dimensione, è per definizione una matrice involutiva.

$\displaystyle I=\begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}$

Possiamo verificare che si tratta di una matrice involutiva elevando la matrice a 2:

$\displaystyle I^2=\begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}\cdot \begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}= \begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}$

Poiché la matrice identità quadrata è la matrice identità, la matrice identità è una matrice involutiva 4×4.

Ovviamente la matrice identità può avere qualsiasi dimensione, poiché è semplicemente una matrice diagonale con tutti gli 1 sulla diagonale principale e il resto 0. Quindi la matrice identità sarà sempre una matrice involutiva, qualunque sia il suo ordine.

Formula della matrice involutiva

Una delle proprietà della matrice involutiva è che la sua formula può essere conosciuta. Ma la dimostrazione della formula per una matrice involutiva del secondo ordine è piuttosto noiosa, quindi ti lasciamo direttamente al risultato, questo è ciò che è veramente importante. Se sei più interessato alla demo, puoi vederla spiegata passo dopo passo qui sotto nei commenti.

La formula per una matrice involutiva di dimensione 2 × 2 è la seguente:

Pertanto, qualsiasi matrice i cui valori della diagonale principale siano opposti e il cui determinante sia -1, sarà una matrice involutiva.

Tuttavia, oltre alle matrici descritte da questa formula, bisogna tenere conto che anche la matrice identità e il suo opposto sono matrici involutive di ordine 2:

$\displaystyle \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix} \qquad \begin{pmatrix} -1 & 0 \\[1.1ex] 0 & -1 \end{pmatrix}$

Proprietà di una matrice involutiva

Le matrici involutive hanno le seguenti caratteristiche:

Il determinante di una matrice involutiva è sempre uguale a -1 o +1.

Esiste una relazione tra matrici involutive e matrici idempotenti : la matrice
$A$

è involutivo se e solo se la matrice

$\displaystyle Q= \cfrac{1}{2} \cdot (A+I)$

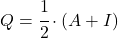
è idempotente.

Sì
$A$

E

$B$

sono due matrici involutive commutanti , quindi il prodotto di matrici

$AB$

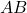
è anche un’altra matrice involutiva.

Qualsiasi potenza di una matrice involutiva si traduce in un’altra matrice involutiva. In particolare una matrice involutiva elevata ad esponente dispari sarà uguale a se stessa, se invece è elevata ad esponente pari sarà equivalente alla matrice Identità.

$A^2 = I$

$A^3 = A$