Unità di identità o matrice

In questa pagina vedrai cos’è la matrice Identità (o Unità) e diversi esempi. Inoltre, spieghiamo quali sono le proprietà della matrice identità, come lavorare con questo tipo di matrice e qual è il risultato del suo determinante. Infine troverai le applicazioni che ha questa matrice molto particolare.

Qual è la matrice identità?

La matrice Identità (o Unità) è una matrice quadrata piena di zeri (0) tranne che sulla diagonale principale, dove tutti gli elementi sono uno (1).

Questa è la definizione di matrice identità o matrice unitaria, ma sicuramente la vedrai più chiaramente attraverso degli esempi:

Esempi di matrici identità

Esempio di matrice identità di dimensione 2 × 2

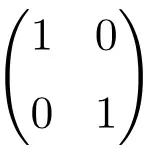
identità unica o matrice di dimensione 2x2

Esempio di matrice Identità di ordine 3×3

identità o matrice unica di dimensione 3x3

Esempio di matrice Identità di dimensione 4×4

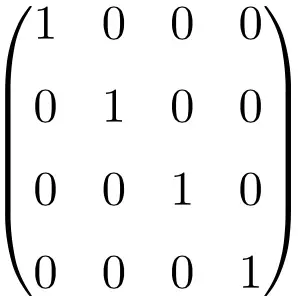
identità o matrice unica di dimensione 4x4

Come puoi vedere, per costruire la matrice identità dobbiamo ancora seguire la stessa procedura: mettere gli uno (1) sulla diagonale principale e il resto tutti zeri (0). L’unica cosa che cambia è la dimensione del tavolo.

Proprietà della tabella identità

La matrice identità, la matrice unitaria o anche la matrice identica è molto utilizzata in matematica, e questo è dovuto alle caratteristiche che questo tipo di matrice possiede:

La matrice identità è un esempio di matrice diagonale .

Una matrice unitaria è sia una matrice triangolare superiore che inferiore.

Anche la matrice identità è una matrice simmetrica .

Il deputato della matrice identitaria è sé stesso.

$\displaystyle \text{Adj}(I) =\begin{pmatrix} 1&0&0\\[1.1ex] 0&1&0 \\[1.1ex] 0&0&1 \end{pmatrix}$

È una matrice invertibile. E, come per l’aggiunto, l’ inverso della matrice Unità è essa stessa:

$\displaystyle I^{-1}=\begin{pmatrix} 1&0&0\\[1.1ex] 0&1&0 \\[1.1ex] 0&0&1 \end{pmatrix}$

Qualsiasi matrice scalare può essere ottenuta dalla moltiplicazione di un numero per la matrice identità:

$\displaystyle 3\cdot \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & 3 \end{pmatrix}$

Tutti gli autovalori (o autovalori) della matrice Identica sono 1:

$\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} \longrightarrow \ \lambda = 1 \ ; \ \lambda = 1 \ ; \ \lambda = 1$

Infine, la matrice identità è anche un esempio di matrice di permutazione .

Operazioni con la matrice Identità (o Unità).

Probabilmente starai pensando: tutto questo è molto bello ma… e a cosa serve la Matrice Identità? Se solo fosse una tabella con 0 e 1!

Anche se potresti non aver ancora trattato questo argomento, la matrice identità è molto utilizzata in matematica, infatti questo tipo di matrice quadrata è molto importante nell’algebra lineare. L’utilità principale della matrice identità è la facilità con cui consente i calcoli delle operazioni sulle matrici. Vediamo quindi come lavorare con la matrice Identità:

Addizioni e sottrazioni con la matrice identità

Un modo per aggiungere (o sottrarre) numeri sulla diagonale principale di una matrice senza modificare gli altri elementi è utilizzare la matrice identità, poiché aggiunge (o sottrae) solo un’unità a quei numeri. elementi:

$\displaystyle \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & 0 & 5 \\[1.1ex] 9 & 6 & -7 \end{pmatrix}+\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 4 & 4 & -1 \\[1.1ex] -2 & 1 & 5 \\[1.1ex] 9 & 6 & -6 \end{pmatrix}$

$\displaystyle \begin{pmatrix} 1 & 7 & 4 \\[1.1ex] 8 & -2 & 3 \\[1.1ex] 0 & 5 & 9 \end{pmatrix}-\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 0 & 7 & 4 \\[1.1ex] 8 & -3 & 3 \\[1.1ex] 0 & 5 & 8 \end{pmatrix}$

Puoi anche aggiungere o sottrarre più unità agli elementi sulla diagonale moltiplicando prima la matrice identità per uno scalare:

$\displaystyle \begin{pmatrix} 3 & 4 & -1 \\[1.1ex] -2 & 0 & 5 \\[1.1ex] 9 & 6 & -7 \end{pmatrix}+5\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} 8 & 4 & -1 \\[1.1ex] -2 & 5 & 5 \\[1.1ex] 9 & 6 & -2 \end{pmatrix}$

$\displaystyle \begin{pmatrix} 1 & 7 & 4 \\[1.1ex] 8 & -2 & 3 \\[1.1ex] 0 & 5 & 9 \end{pmatrix}-4\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} -3 & 7 & 4 \\[1.1ex] 8 & -6 & 3 \\[1.1ex] 0 & 5 & 5 \end{pmatrix}$

Moltiplicazione di una matrice per la matrice identità

Quando si moltiplica una matrice per la matrice identità, agisce come un elemento neutro , ovvero qualsiasi matrice moltiplicata per la matrice identità dà come risultato la stessa matrice. Dai un’occhiata al seguente esempio:

$\displaystyle \begin{pmatrix} -3 & 1 & 0 \\[1.1ex] 5 & 2 & -4 \\[1.1ex] 1 & 0 & 6 \end{pmatrix}\cdot \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} = \begin{pmatrix} -3 & 1 & 0 \\[1.1ex] 5 & 2 & -4 \\[1.1ex] 1 & 0 & 6 \end{pmatrix}$

Inoltre, il significato del prodotto di matrici è irrilevante, o in altre parole, non importa se moltiplichiamo la matrice identità per destra o per sinistra perché il risultato sarà sempre la stessa matrice. Per dimostrarlo, ripetiamo l’esercizio precedente ma questa volta moltiplicando la matrice Identità per il lato opposto:

$\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}\cdot \displaystyle \begin{pmatrix} -3 & 1 & 0 \\[1.1ex] 5 & 2 & -4 \\[1.1ex] 1 & 0 & 6 \end{pmatrix} = \begin{pmatrix} -3 & 1 & 0 \\[1.1ex] 5 & 2 & -4 \\[1.1ex] 1 & 0 & 6 \end{pmatrix}$

Potenza della matrice identità

Il potere della matrice identità risulta sempre nella matrice identità, indipendentemente dall’esponente a cui eleviamo la matrice e dalla dimensione della matrice.

$\left.\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}\right. ^2 =\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

$\left.\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}\right. ^3 =\begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

$\left.\begin{pmatrix} 1 & 0 & 0 & 0\\[1.1ex] 0 & 1 & 0 & 0\\[1.1ex] 0 & 0 & 1 & 0 \\[1.1ex] 0& 0 &0&1\end{pmatrix}\right. ^5 =\begin{pmatrix} 1 & 0 & 0 & 0\\[1.1ex] 0 & 1 & 0 & 0\\[1.1ex] 0 & 0 & 1 & 0 \\[1.1ex] 0& 0 &0&1\end{pmatrix}$

$\left.\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}\right. ^n =\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

Determinante della matrice identità

Come presumo tu abbia già immaginato, il determinante della matrice Identità (o Unità) è sempre uguale a 1 , indipendentemente dalla dimensione della matrice.

$\displaystyle\begin{vmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{vmatrix} = \bm{1}$

$\displaystyle\begin{vmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{vmatrix}=\bm{1}$

$\displaystyle\begin{vmatrix} 1 & 0 & 0 & 0 \\[1.1ex] 0 & 1 & 0 & 0 \\[1.1ex] 0 & 0 & 1 & 0 \\[1.1ex] 0 & 0 & 0 & 1 \end{vmatrix}=\bm{1}$

Applicazioni della matrice di identità

Infine, dopo tutte queste informazioni, probabilmente già saprai come rispondere alla tipica domanda: perché la matrice identitaria è così importante? Tranquilli, anch’io mi sono posto questa domanda in passato. 😂

Come avrai notato, la matrice identità ha molti usi ed è per questo che è così interessante. Uno degli usi della matrice Unit è quello delle operazioni, perché, come abbiamo visto, è molto semplice eseguire operazioni sulle matrici con essa.

D’altra parte, la matrice identità viene utilizzata anche per risolvere equazioni di matrice . Per fare ciò, utilizziamo la seguente proprietà della matrice inversa: moltiplicare una matrice per la sua matrice inversa è uguale alla matrice identità. Puoi vedere come risolvere un’equazione con le matrici facendo clic sul collegamento.

Inoltre, la matrice identità viene utilizzata anche per calcolare la matrice inversa con il metodo gaussiano. Questo metodo prevede di posizionare una matrice accanto alla matrice identità, formando così una matrice più grande. Successivamente, la matrice originale deve essere trasformata in una matrice identità applicando operazioni elementari sulle righe. Sembra molto complicato ma in realtà non lo è molto, comunque occorre applicare tutta una procedura, quindi se sei più interessato puoi cercare come invertire una matrice nel motore di ricerca della pagina web (in alto a DESTRA).

Infine, la matrice Identità è utile anche per diagonalizzare una matrice e calcolarne gli autovalori (o autovalori). Perché mediante alcune operazioni, in cui interviene la matrice unitaria, si può ottenere il polinomio caratteristico da cui si ottengono gli autovalori. Ma è già un argomento molto avanzato, ecco perché abbiamo un’intera pagina super completa dedicata alla diagonalizzazione delle matrici con esempi ed esercizi risolti che la spiegano. Se sei più interessato, puoi cercare questa guida nel nostro motore di ricerca (in alto a destra).

Identità o unità di matrice