Matrice hermitiana (o hermitiana).

In questa pagina puoi scoprire cos’è una matrice Hermitiana, nota anche come matrice Hermitiana. Troverai esempi di matrici hermitiane, tutte le loro proprietà e la forma che hanno questi tipi di matrici per comprenderle perfettamente. Infine, spiegheremo anche come scomporre qualsiasi matrice complessa nella somma di una matrice Hermitiana più una matrice anti-Hermitiana.

Cos’è una matrice hermitiana o hermitiana?

Una matrice Hermitiana , o detta anche matrice Hermitiana, è una matrice quadrata di numeri complessi che ha la caratteristica di essere uguale alla sua trasposta coniugata .

A=A^*

Oro

A^*

è la matrice di trasposizione coniugata di

A

.

Per curiosità, questo tipo di matrice prende il nome in onore di Charles Hermite, un matematico francese del XIX secolo che fece importanti ricerche in matematica, in particolare nel campo dell’algebra lineare.

Il motivo per cui questa matrice è stata chiamata in questo modo è che mostra che gli autovalori (o gli autovalori) di queste particolari matrici sono sempre numeri reali, ma lo spiegheremo più in dettaglio in Proprietà delle matrici hermitiane.

Infine, questa matrice può talvolta essere definita anche matrice autoaggiunta, sebbene ciò sia molto raro.

Esempi di matrici hermitiane

Una volta vista la definizione di matrice Hermitiana (o matrice Hermitiana), vediamo alcuni esempi di matrici Hermitiane di diverse dimensioni:

Esempio di matrice Hermitiana di ordine 2×2

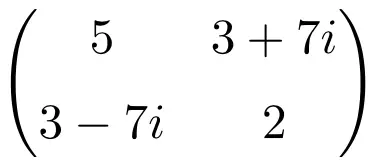
Matrice Hermitiana o Hermitiana di dimensione 2x2

Esempio di matrice hermitiana di dimensione 3 × 3

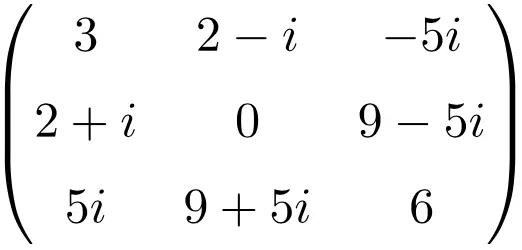
Matrice Hermitiana o Hermitiana di dimensione 3x3

Esempio di matrice Hermitiana di dimensione 4×4

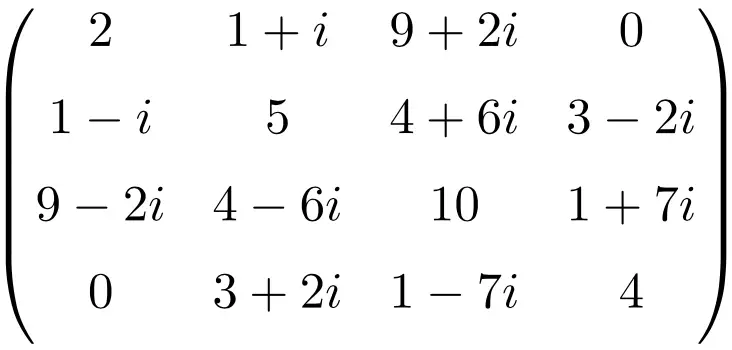
Matrice Hermitiana o Hermitiana di dimensione 4x4

Tutte queste matrici sono hermitiane perché la matrice di trasposizione coniugata di ciascuna è uguale alla matrice stessa.

Struttura di una matrice Hermitiana

Le matrici Hermitiane hanno una struttura molto facile da ricordare: sono costituite da numeri reali sulla diagonale principale, e l’elemento complesso situato nella i-esima riga e nella j-esima colonna deve essere il coniugato dell’elemento che si trova nella j-esima riga e l’iesima colonna.

Ecco alcuni esempi di strutture di matrice Hermitiana.

Struttura hermitiana 2×2

\displaystyle \begin{pmatrix}a& b\\[1.1ex] \overline{b} & c \end{pmatrix}

Struttura hermitiana 3×3

\displaystyle \begin{pmatrix}a& b & c \\[1.1ex] \overline{b} & d & e \\[1.1ex] \overline{c} & \overline{e} & f\end{pmatrix}

Struttura Hermitiana 4×4

\displaystyle \begin{pmatrix}a& b & c & d \\[1.1ex] \overline{b} & e & f & g \\[1.1ex] \overline{c} & \overline{f} & h & i \\[1.1ex] \overline{d} & \overline{g} & \overline{i} & j \end{pmatrix}

Proprietà della matrice hermitiana

Vedremo ora quali sono le proprietà di questo tipo di matrice quadrata complessa:

  • Qualsiasi matrice Hermitiana è una matrice normale . Sebbene non tutte le matrici normali siano matrici hermitiane.
  • Qualsiasi matrice Hermitiana è diagonalizzabile. Inoltre, la matrice diagonale risultante contiene solo elementi reali.
  • Pertanto gli autovalori (o autovalori) di una matrice hermitiana sono sempre numeri reali. Questa proprietà fu scoperta da Charles Hermite, e per questo motivo ebbe l’onore di chiamare Hermitiana questa matrice così speciale.
  • Allo stesso modo, gli autospazi di una matrice hermitiana sono ortogonali a due a due: esiste una base ortonormale di

    \mathbb{C}^n

    costituito da autovettori (autovettori) della matrice.

  • Una matrice di numeri reali, vale a dire che nessun elemento ha una parte immaginaria, è hermitiana se e solo se è una matrice simmetrica. Come ad esempio la matrice identità 2×2 .
  • Una matrice hermitiana può essere espressa come la somma di una matrice simmetrica reale e di una matrice antisimmetrica immaginaria.

A =B+Ci

  • La somma (o sottrazione) di due matrici Hermitiane è uguale ad un’altra matrice Hermitiana, perché:

(A\pm B)^* = A^*\pm B^* = A \pm B

  • Il risultato del prodotto di una matrice Hermitiana per uno scalare è un’altra matrice Hermitiana se lo scalare è un numero reale.

(k \cdot A)^* = \overline{k}\cdot A^* = k \cdot A

  • Il prodotto di due matrici hermitiane generalmente non è più hermitiano. Tuttavia il prodotto è hermitiano quando le due matrici sono commutabili, cioè quando il risultato della moltiplicazione delle due matrici è lo stesso indipendentemente dalla direzione in cui vengono moltiplicate, perché allora la seguente condizione delle operazioni con trasposizione coniugata matrici:

(A \cdot B)^* = B^*\cdot A^* = B \cdot A = A \cdot B

  • Se una matrice Hermitiana è invertibile, anche la sua inversa risulta essere una matrice Hermitiana.

(A^{-1})^* = (A^*)^{-1} = A^{-1}

  • Il determinante di una matrice hermitiana è sempre equivalente a un numero reale. Ecco la prova di questa proprietà:

det(A) = det(A^t) \ \longrightarrow \ det(A^*) = \overline{det(A)}

Assetato

A = A^*

:

det(A) = \overline{det(A)}

Pertanto, affinché questa condizione sia soddisfatta, il determinante di una matrice hermitiana deve necessariamente essere un numero reale. In questo modo il coniugato del risultato è uguale al risultato stesso.

Scomposizione di una matrice complessa in una matrice Hermitiana e una matrice anti-Hermitiana

Qualsiasi matrice con elementi complessi può essere scomposta nella somma di una matrice Hermitiana più un’altra matrice anti-Hermitiana . Ma per questo è necessario conoscere le seguenti particolarità di questi tipi di matrici:

  • La somma di una matrice quadrata complessa più il suo coniugato trasposto dà una matrice hermitiana.

C + C^* = \text{Matriz Hermitiana}

  • La differenza tra una matrice quadrata complessa e il suo coniugato trasposto dà una matrice anti-Hermitiana (o anti-Hermitiana).

C - C^* = \text{Matriz Antihermitiana}

  • Pertanto, tutte le matrici complesse possono essere scomposte nella somma di una matrice Hermitiana e di una matrice anti-Hermitiana. Questo teorema è noto come decomposizione di Teoplitz :

\displaystyle \begin{array}{c} C = A + B \\[2ex] A = \cfrac{1}{2}\cdot (C+C^*) \qquad B = \cfrac{1}{2} \cdot (C-C^*)\end{array}

Dove C è la matrice complessa che vogliamo scomporre, C* il suo coniugato trasposto, ed infine A e B sono rispettivamente le matrici Hermitiana e AntiHermitiana in cui viene scomposta la matrice C.

Lascia un commento

Il tuo indirizzo email non sarà pubblicato. I campi obbligatori sono contrassegnati *

Torna in alto