Matrice diagonale - Mathority

In questa pagina vedrai cos’è una matrice diagonale ed esempi di matrici diagonali. Inoltre, scoprirai come operare con questo tipo di matrici, come calcolare facilmente i loro determinanti e come invertirli. Esistono anche proprietà e applicazioni delle matrici diagonali. E, infine, ci sono le spiegazioni di una matrice bidiagonale e di una matrice tridiagonale.

Cos’è una matrice diagonale?

Una matrice diagonale è una matrice quadrata in cui tutti gli elementi non sulla diagonale principale sono zero (0). Gli elementi della diagonale principale possono essere zero o meno.

Una volta conosciuta l’esatta definizione di matrice diagonale, vedremo esempi di matrici diagonali:

Esempi di matrici diagonali

Esempio di matrice diagonale di dimensione 2 × 2

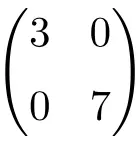
Esempio di matrice diagonale di ordine 3×3

Esempio di matrice diagonale di dimensione 4×4

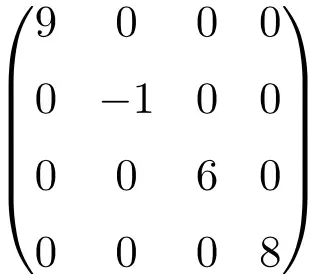
Questi tipi di matrici vengono generalmente scritte indicando gli elementi della diagonale:

$diag(2,5,1) = \left. \begin{pmatrix} 2 & 0 & 0 \\[1.1ex] 0 & 5 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

Operazioni con matrici diagonali

Uno dei motivi per cui le matrici diagonali sono così importanti per l’algebra lineare è la facilità con cui consentono di eseguire calcoli. Questo è il motivo per cui sono così usati in matematica.

Somma e sottrazione di matrici diagonali

Aggiungere (e sottrarre) due matrici diagonali è molto semplice: basta aggiungere (o sottrarre) i numeri sulle diagonali.

$\displaystyle \text{diag}(a_1,... ,a_n) \pm \text{diag}(b_1 ,... , b_n) = \text{diag}(a_1\pm b_1,..., a_n\pm b_n)$

Per esempio:

$\displaystyle \begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 0 & -2 & 0 \\[1.1ex] 0 & 0 & 6 \end{pmatrix} +\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & -4 \end{pmatrix} = \begin{pmatrix} 6& 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 2 \end{pmatrix}$

Moltiplicazione di matrici diagonali

Per risolvere una moltiplicazione o un prodotto matriciale di due matrici diagonali, moltiplica semplicemente tra loro gli elementi delle diagonali.

$\displaystyle \text{diag}(a_1,... ,a_n) \cdot \text{diag}(b_1 ,... , b_n) = \text{diag}(a_1\cdot b_1,..., a_n\cdot b_n)$

Per esempio:

$\displaystyle \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & -4 & 0 \\[1.1ex] 0 & 0 & -3 \end{pmatrix} \cdot\begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 0 & -2 & 0 \\[1.1ex] 0 & 0 & 6 \end{pmatrix} = \begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 0 & 8 & 0 \\[1.1ex] 0 & 0 & -18 \end{pmatrix}$

Potenze di matrici diagonali

Per calcolare la potenza di una matrice diagonale dobbiamo elevare ogni elemento della diagonale all’esponente:

$\displaystyle A= \text{diag}(a_1,... ,a_n)$

$\displaystyle A^k= \text{diag}(a_1^k,... ,a_n^k)$

Per esempio:

$\displaystyle\left. \begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 2 & 0 \\[1.1ex] 0 & 0 & 4 \end{pmatrix}\right.^3= \begin{pmatrix} 27 & 0 & 0 \\[1.1ex] 0 & 8 & 0 \\[1.1ex] 0 & 0 & 64 \end{pmatrix}$

Determinante di una matrice diagonale

Il determinante di una matrice diagonale è il prodotto degli elementi sulla diagonale principale.

$\displaystyle A= \text{diag}(a_1,... ,a_n)$

$\displaystyle \text{det}(A)= \prod_{i =1}^n a_i$

Osserva il seguente esercizio risolto in cui troviamo il determinante di una matrice diagonale semplicemente moltiplicando gli elementi della sua diagonale principale:

$\displaystyle \begin{vmatrix} 5 & 0 & 0 \\[1.1ex] 0 & 2 & 0 \\[1.1ex] 0 & 0 & 3 \end{vmatrix} = 5 \cdot 2 \cdot 3 = 30$

Questo teorema è facile da dimostrare: basta calcolare il determinante di una matrice diagonale per blocchi (o cofattori). Questa dimostrazione è dettagliata di seguito utilizzando una matrice diagonale generica:

$\begin{aligned} \begin{vmatrix} a & 0 & 0 \\[1.1ex] 0 & b & 0 \\[1.1ex] 0 & 0 & c \end{vmatrix}& = a \cdot \begin{vmatrix} b & 0 \\[1.1ex] 0 & c \end{vmatrix} - 0 \cdot \begin{vmatrix} 0 & 0 \\[1.1ex] 0 & c \end{vmatrix} + 0 \cdot \begin{vmatrix} 0 & b \\[1.1ex] 0 & 0 \end{vmatrix} \\[2ex] & =a \cdot (b\cdot c) - 0 \cdot 0 + 0 \cdot 0 \\[2ex] & = a \cdot b \cdot c \end{aligned}$

Invertire una matrice diagonale

Una matrice diagonale è invertibile se e solo se tutti gli elementi della diagonale principale sono diversi da 0 . In questo caso diciamo che la matrice diagonale è una matrice regolare.

Inoltre, l’inverso di una matrice diagonale sarà sempre un’altra matrice diagonale con gli inversi della diagonale principale:

$\displaystyle A= \begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 2 & 0 \\[1.1ex] 0 & 0 & 8 \end{pmatrix} \ \longrightarrow \ A^{-1}=\begin{pmatrix} \frac{1}{3} & 0 & 0 \\[1.1ex] 0 & \frac{1}{2} & 0 \\[1.1ex] 0 & 0 & \frac{1}{8} \end{pmatrix}$

Dalla caratteristica precedente si deduce che il determinante dell’inversa di una matrice diagonale è il prodotto delle inverse della diagonale principale:

$\displaystyle B= \begin{pmatrix} 2 & 0 & 0 \\[1.1ex] 0 & 4 & 0 \\[1.1ex] 0 & 0 & -1 \end{pmatrix}$

$\displaystyle\left| B^{-1}\right|=\cfrac{1}{2} \cdot \cfrac{1}{4} \cdot \cfrac{1}{-1}=-\cfrac{1}{8} = -0,125$

Proprietà delle matrici diagonali

Qualsiasi matrice diagonale è anche una matrice simmetrica .

Una matrice diagonale è una matrice triangolare sia superiore che inferiore .

La matrice identità è una matrice diagonale:

$\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

Allo stesso modo, anche la matrice zero è una matrice diagonale, perché tutti i suoi elementi che non sono sulla diagonale sono zeri. Sebbene i numeri sulla diagonale siano 0.

$\begin{pmatrix} 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \end{pmatrix}$

Gli autovalori (o autovalori) di una matrice diagonale sono gli elementi della sua diagonale principale.

$\begin{pmatrix} 7 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & 4 \end{pmatrix} \longrightarrow \ \lambda = 3 \ ; \ \lambda = 4 \ ; \ \lambda = 7$

Una matrice quadrata è diagonale se e solo se è triangolare e normale .

L’ aggiunto di una matrice diagonale è un’altra matrice diagonale.

Applicazioni della matrice diagonale

Come abbiamo visto, risolvere i calcoli con matrici diagonali è molto semplice, perché nelle operazioni sono coinvolti molti zeri. Per questo motivo sono molto utili nel campo della matematica e trovano largo impiego.

Per questo stesso motivo sono stati fatti tanti studi su come diagonalizzare una matrice ed è stato addirittura sviluppato un metodo per diagonalizzare le matrici (utilizzando il polinomio caratteristico).

Pertanto anche le matrici diagonalizzabili sono abbastanza rilevanti. Come il teorema della decomposizione spettrale, che stabilisce le condizioni per cui una matrice può essere diagonalizzata e quando non lo è.

matrice bidiagonale

Una matrice bidiagonale è una matrice quadrata in cui tutti gli elementi che non si trovano sulla diagonale principale o sulla diagonale superiore o inferiore sono 0.

Per esempio:

$\begin{pmatrix} 3 & 2 & 0 \\[1.1ex] 0 & -5 & 1 \\[1.1ex] 0 & 0 & 6 \end{pmatrix}$

matrice bidiagonale superiore

$\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 6 & 2 & 0 \\[1.1ex] 0 & 7 & 4 \end{pmatrix}$

matrice bidiagonale inferiore

Quando la diagonale principale e la prima superdiagonale sono occupate si parla di matrice bidiagonale superiore. Quando invece sono occupate la diagonale principale e la prima sottodiagonale, si parla di matrice bidiagonale inferiore.

matrice tridiagonale

Una matrice tridiagonale è una matrice quadrata i cui unici elementi diversi da zero sono quelli della diagonale principale e delle diagonali adiacenti sopra e sotto.

Per esempio:

$\begin{pmatrix} 2 & 3 & 0 & 0 \\[1.1ex] -4 & 5 & 9 & 0 \\[1.1ex] 0 & 1 & 6 & -2 \\[1.1ex] 0 & 0 & 8 & 7 \end{pmatrix}$

Pertanto, tutte le matrici diagonali, bidiagonali e tridiagonali sono esempi di matrici di bande . Perché una matrice di bande è quella matrice che ha tutti i suoi elementi diversi da zero attorno alla diagonale principale.

Cos’è una matrice diagonale?

Esempi di matrici diagonali

Operazioni con matrici diagonali

Somma e sottrazione di matrici diagonali

Moltiplicazione di matrici diagonali

Potenze di matrici diagonali

Determinante di una matrice diagonale

Invertire una matrice diagonale

Proprietà delle matrici diagonali

Applicazioni della matrice diagonale

matrice bidiagonale

matrice tridiagonale

Lascia un commento Annulla risposta