Matrice dell'Assia (o Assia) -

Questa pagina è sicuramente la spiegazione più completa esistente della matrice dell’Assia. Qui viene spiegato il concetto di matrice Hessiana, come calcolarla con esempi e ci sono anche diversi esercizi risolti per esercitarsi. Inoltre, potrai scoprire come vengono calcolati i valori massimo e minimo di una funzione multivariabile e se si tratta di una funzione concava o convessa. Infine, troverai anche le utilità e le applicazioni della matrice dell’Assia.

Cos’è la matrice dell’Assia?

La definizione della matrice dell’Assia (o dell’Assia) è la seguente:

La matrice Hessiana è una matrice quadrata di dimensione n × n composta dalle derivate seconde parziali di una funzione di n variabili.

Questa matrice è conosciuta anche come Hessiana, o anche in alcuni libri di matematica viene chiamata Discriminante. Ma il modo più comune per chiamarla è matrice dell’Assia.

La formula per la matrice Hessiana è quindi la seguente:

Formula della matrice dell'Assia o dell'Assia

Pertanto, la matrice Hessiana sarà sempre una matrice quadrata la cui dimensione sarà uguale al numero di variabili nella funzione. Ad esempio, se la funzione ha 3 variabili, la matrice dell’Assia avrà dimensione 3×3.

Inoltre il teorema di Schwarz (o teorema di Clairaut) dice che l’ordine di differenziazione non ha importanza, cioè derivare parzialmente per primo rispetto alla variabile

$x_1$

quindi rispetto alla variabile

$x_2$

equivale a differenziare parzialmente rispetto a

$x_2$

quindi rispetto

$x_1$

$\displaystyle \cfrac{\partial^2 f}{\partial x_i\partial x_j} = \cfrac{\partial^2 f}{\partial x_j\partial x_i}$

Pertanto, la matrice Hessiana è una matrice simmetrica , o in altre parole, ha una simmetria il cui asse è la sua diagonale principale.

Per curiosità, la matrice dell’Assia prende il nome da Ludwig Otto Hesse, un matematico tedesco del XIX secolo che diede contributi molto importanti al campo dell’algebra lineare.

Esempio di calcolo della matrice Hessiana

Vediamo un esempio di come trovare una matrice Hessiana di dimensione 2×2:

Calcola la matrice dell’Assia nel punto (1,0) della seguente funzione:

$\displaystyle f(x,y)=y^4+x^3+3x^2+ 4y^2 -4xy -5y +8$

Per prima cosa dobbiamo calcolare le derivate parziali del primo ordine:

$\displaystyle \cfrac{\partial f}{\partial x} = 3x^2 +6x -4y$

$\displaystyle \cfrac{\partial f}{\partial y} = 4y^3+8y -4x -5$

Una volta conosciute le derivate prime, calcoliamo tutte le derivate parziali del secondo ordine:

$\displaystyle \cfrac{\partial^2 f}{\partial x^2} = 6x +6$

$\displaystyle \cfrac{\partial^2 f}{\partial y^2} =12y^2 +8$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial y} = \cfrac{\partial^2 f}{\partial y \partial x}= -4$

Pertanto, ora possiamo trovare la matrice Hessiana dalla formula per le matrici 2 × 2:

$\displaystyle H_f (x,y)=\begin{pmatrix}\cfrac{\partial^2 f}{\partial x^2} & \cfrac{\partial^2 f}{\partial x \partial y} \\[4ex] \cfrac{\partial^2 f}{\partial y \partial x} & \cfrac{\partial^2 f}{\partial y^2} \end{pmatrix}$

$\displaystyle H_f (x,y)=\begin{pmatrix}6x +6 &-4 \\[2ex] -4 & 12y^2+8 \end{pmatrix}$

Pertanto la matrice Hessiana valutata al punto (1,0) sarà:

$\displaystyle H_f (1,0)=\begin{pmatrix}6(1) +6 &-4 \\[2ex] -4 & 12(0)^2+8 \end{pmatrix}$

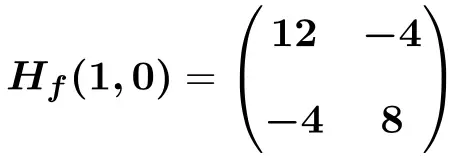
Problemi risolti delle matrici Hessiane

Esercizio 1

Calcola la matrice Hessiana della seguente funzione con 2 variabili nel punto (1,1):

$\displaystyle f(x,y)=x^2y+y^2x$

vedi soluzione

Per prima cosa dobbiamo trovare le derivate parziali del primo ordine della funzione:

$\displaystyle \cfrac{\partial f}{\partial x} = 2xy+y^2$

$\displaystyle \cfrac{\partial f}{\partial y} = x^2+2yx$

Una volta che abbiamo già calcolato le derivate prime, procediamo a risolvere tutte le derivate parziali del secondo ordine:

$\displaystyle \cfrac{\partial^2 f}{\partial x^2} = 2y$

$\displaystyle \cfrac{\partial^2 f}{\partial y^2} =2x$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial y} = \cfrac{\partial^2 f}{\partial y \partial x}=2x+2y$

Pertanto la matrice Hessiana è definita come segue:

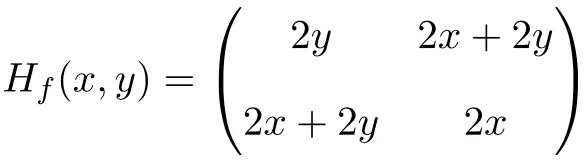
Esercizio risolto della matrice Hessiana o matrice Hessiana di dimensione 2x2

Infine non resta che valutare la matrice Hessiana al punto (1,1):

$\displaystyle H_f (1,1)=\begin{pmatrix}2\cdot 1 &2 \cdot 1+2\cdot 1 \\[1.5ex] 2\cdot 1+2\cdot 1 & 2\cdot 1 \end{pmatrix}$

$\displaystyle \bm{H_f (1,1)}=\begin{pmatrix}\bm{2} & \bm{4} \\[1.1ex] \bm{4} & \bm{2} \end{pmatrix}$

Esercizio 2

Calcola l’Assia nel punto (1,1) della seguente funzione in due variabili:

$\displaystyle f(x,y)= e^{y\ln x}$

vedi soluzione

Per prima cosa dobbiamo calcolare le derivate parziali del primo ordine della funzione:

$\displaystyle \cfrac{\partial f}{\partial x} = e^{y\ln x} \cdot \cfrac{y}{x}$

$\displaystyle \cfrac{\partial f}{\partial y} = e^{y\ln x} \cdot \ln x$

Una volta ottenute le derivate prime, calcoliamo le derivate parziali del secondo ordine della funzione:

$\displaystyle \cfrac{\partial^2 f}{\partial x^2} = e^{y\ln x} \cdot \cfrac{y^2}{x^2} - e^{y\ln x} \cdot \cfrac{y}{x^2}$

$\displaystyle \cfrac{\partial^2 f}{\partial y^2} =e^{y\ln x} \cdot \ln ^2 x$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial y}=\cfrac{\partial^2 f}{\partial y \partial x} =e^{y\ln x} \cdot \cfrac{y}{x}\cdot \ln x + e^{y\ln x}\cdot \cfrac{1}{x}$

Pertanto la matrice Hessiana della funzione è una matrice quadrata di dimensione 2×2:

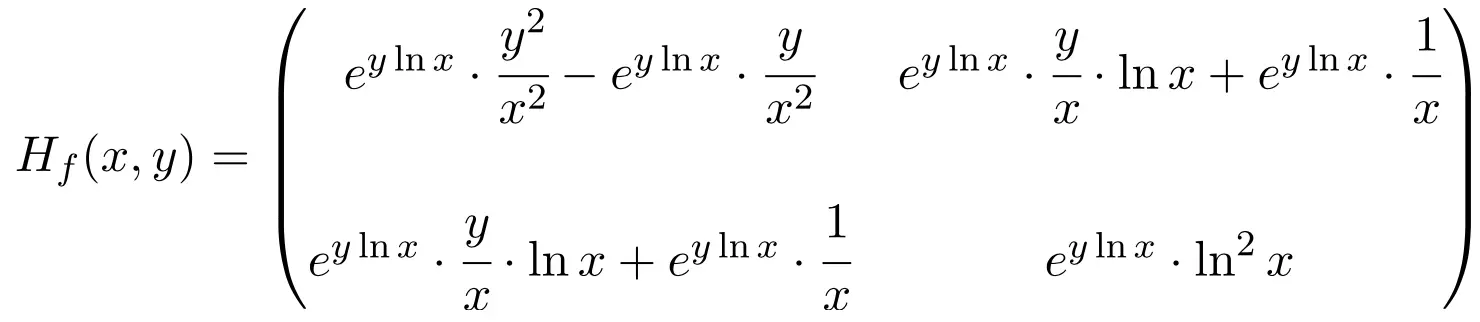
Risolto Esercizio Hessiano o matrice Hessiana di dimensione 2x2

Infine non resta che valutare la matrice Hessiana al punto (1,1):

$\displaystyle H_f (1,1)=\begin{pmatrix} e^{1\ln (1)} \displaystyle \cdot \cfrac{1^2}{1^2} - e^{1\ln (1)} \cdot \cfrac{1}{1^2}& e^{1\ln (1)} \cdot \cfrac{1}{1}\cdot \ln (1) + e^{1\ln (1)}\cdot \cfrac{1}{1} \\[3ex] e^{1\ln (1)} \cdot \cfrac{1}{1}\cdot \ln (1) + e^{1\ln (1)}\cdot \cfrac{1}{1} & e^{1\ln (1)} \cdot \ln ^2 (1) \end{pmatrix}$

$\displaystyle H_f (1,1)=\begin{pmatrix}e^{0} \cdot 1 - e^{0} \cdot 1& e^{0} \cdot 1\cdot 0 + e^{0}\cdot 1 \\[2ex] e^{0} \cdot 1\cdot 0 + e^{0}\cdot 1 & e^{0} \cdot 0\end{pmatrix}$

$\displaystyle H_f (1,1)=\begin{pmatrix}1 - 1& 0+ 1 \\[1.5ex] 0 +1 & 1 \cdot 0\end{pmatrix}$

$\displaystyle \bm{H_f (1,1)}=\begin{pmatrix}\bm{0} & \bm{1} \\[1.1ex] \bm{1} & \bm{0} \end{pmatrix}$

Esercizio 3

Trova la matrice Hessiana nel punto

$(0,1,\pi)$

della seguente funzione con 3 variabili:

$\displaystyle f(x,y,z)= e^{-x}\cdot \text{sen}(yz)$

vedi soluzione

Per prima cosa calcoliamo le derivate parziali del primo ordine della funzione:

$\displaystyle \cfrac{\partial f}{\partial x} = -e^{-x}\cdot \text{sen}(yz)$

$\displaystyle \cfrac{\partial f}{\partial y} = ze^{-x}\cdot \text{cos}(yz)$

$\displaystyle \cfrac{\partial f}{\partial z} = ye^{-x}\cdot \text{cos}(yz)$

Una volta ottenute le derivate prime, calcoliamo le derivate parziali del secondo ordine della funzione:

$\displaystyle \cfrac{\partial^2 f}{\partial x^2} =e^{-x}\cdot \text{sen}(yz)$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial y}=\cfrac{\partial^2 f}{\partial y \partial x} =-ze^{-x}\cdot \text{cos}(yz)$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial z}=\cfrac{\partial^2 f}{\partial z \partial x} =-ye^{-x}\cdot \text{cos}(yz)$

$\displaystyle \cfrac{\partial^2 f}{\partial y^2} =-z^2e^{-x}\cdot \text{sen}(yz)$

$\displaystyle \cfrac{\partial^2 f}{\partial y \partial z}=\cfrac{\partial^2 f}{\partial z \partial y} =e^{-x}\cdot \text{cos}(yz)-yze^{-x}\cdot \text{sen}(yz)$

$\displaystyle \cfrac{\partial^2 f}{\partial^2 z} = -y^2e^{-x}\cdot \text{sen}(yz)$

Quindi la matrice Hessiana della funzione è una matrice quadrata di dimensione 3×3:

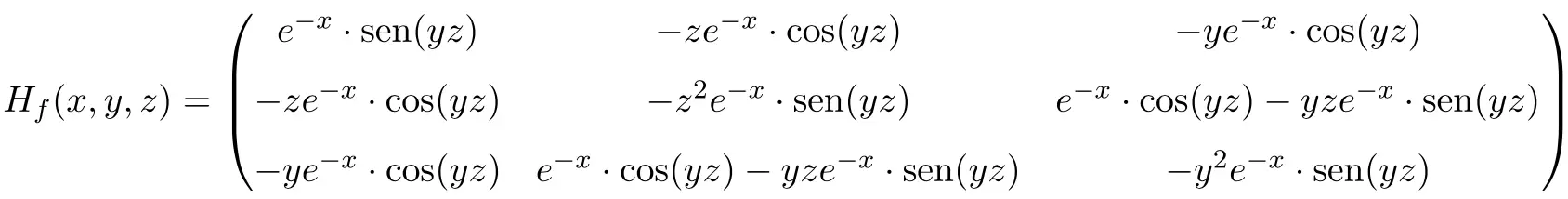
esempio di tela o matrice di tela di dimensione 3x3

Infine, sostituiamo le variabili con i rispettivi valori nel punto

$(0,1,\pi):$

$\displaystyle H_f(0,1,\pi)=\begin{pmatrix}e^{-0}\cdot \text{sen}(1\pi) & -\pi e^{-0}\cdot \text{cos}(1\pi) &-1e^{-0}\cdot \text{cos}(1\pi) \\[1.5ex] -\pi e^{-0}\cdot \text{cos}(1 \pi)&-\pi^2e^{-0}\cdot \text{sen}(1 \pi) &e^{-0}\cdot \text{cos}(1 \pi)-1 \pi e^{-0}\cdot \text{sen}(1 \pi) \\[1.5ex] -1e^{-0}\cdot \text{cos}(1 \pi)& e^{-0}\cdot \text{cos}(1 \pi)-1 \pi e^{-0}\cdot \text{sen}(1 \pi)& -1^2e^{-0}\cdot \text{sen}(1 \pi) \end{pmatrix}$

$\displaystyle H_f(0,1,\pi)=\begin{pmatrix}1\cdot 0 & -\pi \cdot 1 \cdot (-1)&-1\cdot 1 \cdot (-1) \\[1.5ex] -\pi \cdot 1 \cdot (-1) &-\pi^2\cdot 1\cdot 0 &1 \cdot (-1)-\pi \cdot 1\cdot 0 \\[1.5ex] -1\cdot 1 \cdot (-1) & 1\cdot (-1) - \pi \cdot 1\cdot 0 & -1\cdot 1 \cdot 0 \end{pmatrix}$

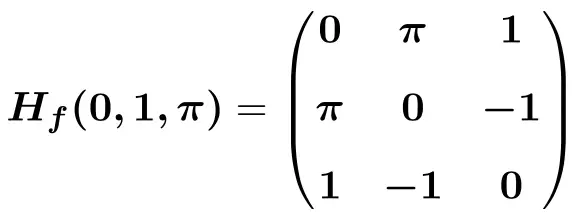
esercizio risolto passo passo su matrice Hessiana o matrice Hessiana di dimensione 3x3

Esercizio 4

Determina la matrice dell’Assia nel punto (2,-1,1,-1) della seguente funzione con 4 variabili:

$\displaystyle f(x,y,z,w)= 2x^3y^4zw^2 - 2y^3w^4+ 3x^2z^2$

vedi soluzione

Il primo passo è trovare le derivate parziali del primo ordine della funzione:

$\displaystyle \cfrac{\partial f}{\partial x} =6x^2y^4zw^2 + 6xz^2$

$\displaystyle \cfrac{\partial f}{\partial y} =8x^3y^3zw^2 - 6y^2w^4$

$\displaystyle \cfrac{\partial f}{\partial z} = 2x^3y^4w^2 + 6x^2z$

$\displaystyle \cfrac{\partial f}{\partial w} =4x^3y^4zw - 8y^3w^3$

Ora risolviamo le derivate parziali del secondo ordine della funzione:

$\displaystyle \cfrac{\partial^2 f}{\partial x^2} =12xy^4zw^2 + 6z^2$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial y}=\cfrac{\partial^2 f}{\partial y \partial x}=24x^2y^3zw^2$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial z}=\cfrac{\partial^2 f}{\partial z \partial x}=6x^2y^4w^2 + 12xz$

$\displaystyle \cfrac{\partial^2 f}{\partial x \partial w} = \cfrac{\partial^2 f}{\partial w \partial x}=12x^2y^4zw$

$\displaystyle \cfrac{\partial^2 f}{\partial y^2} =24x^3y^2zw^2 - 12yw^4$

$\displaystyle \cfrac{\partial^2 f}{\partial y \partial z}=\cfrac{\partial^2 f}{\partial y \partial z}=8x^3y^3w^2$

$\displaystyle \cfrac{\partial^2 f}{\partial y \partial w} = \cfrac{\partial^2 f}{\partial w \partial y}=16x^3y^3zw - 24y^2w^3$

$\displaystyle \cfrac{\partial^2 f}{\partial^2 z} =6x^2$

$\displaystyle \cfrac{\partial^2 f}{\partial z \partial w} = \cfrac{\partial^2 f}{\partial w \partial z}=4x^3y^4w$

$\displaystyle \cfrac{\partial^2 f}{\partial^2 w} =4x^3y^4z - 24y^3w^2$

Pertanto l’espressione della matrice Hessiana 4×4 ottenuta risolvendo tutte le derivate parziali è la seguente:

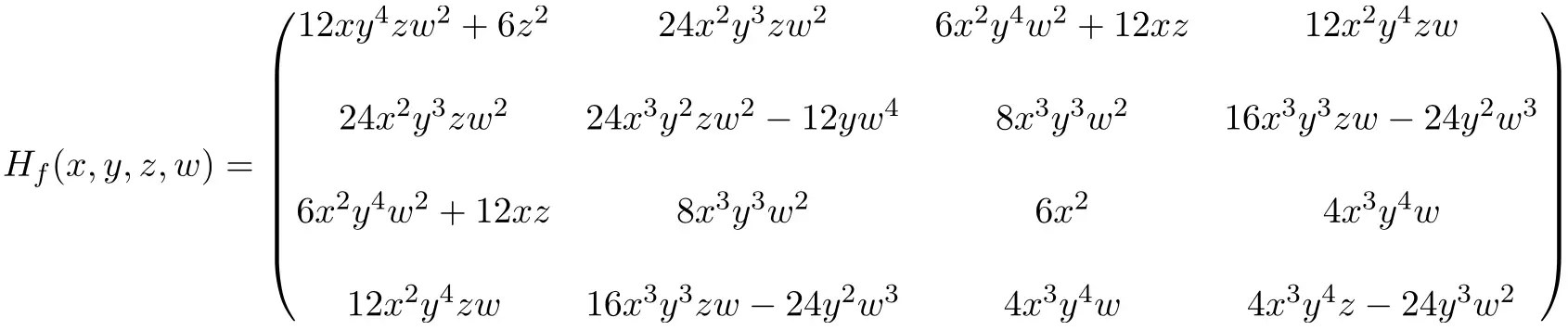
esempio risolto passo dopo passo di tela o matrice di tela di dimensione 4x4

Infine sostituiamo le incognite con i rispettivi valori in punti (2,-1,1,-1) ed eseguiamo i calcoli:

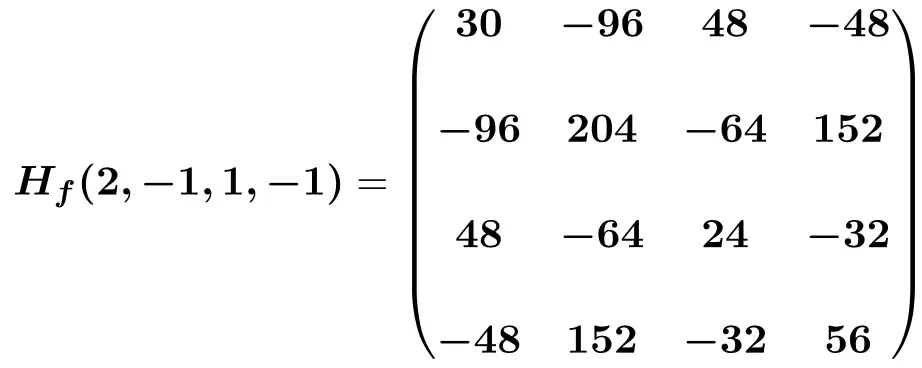
Esercizio risolto passo passo su matrice Hessiana o matrice Hessiana di dimensione 4x4

Come fai a sapere quando la matrice dell’Assia è positiva, negativa o indefinita?

Come vedremo più avanti, è molto utile sapere se la matrice hessiana è una matrice semidefinita positiva, definita positiva, semidefinita negativa, definita negativa o indefinita. Vediamo quindi come scoprirlo:

Criterio degli autovalori (o autovalori)

Un modo per sapere di che tipo di matrice si tratta è esaminare gli autovalori (o autovalori) della matrice assiana:

La matrice Hessiana è semidefinita positiva se ha autovalori (o autovalori) uguali e maggiori di zero. Vale a dire che ha autovalori positivi e almeno uno uguale a 0:

$\lambda \geq 0$

La matrice Hessiana è definita positiva se tutti i suoi autovalori (o autovalori) sono esclusivamente maggiori di 0 (positivi):

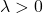$\lambda > 0″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”43″ style=”vertical-align: -2px;”></p> </p> <ul> <li> La matrice Hessiana è <span style=$ semidefinita negativa se ha autovalori (o autovalori) uguali e inferiori a zero. Vale a dire che ha autovalori negativi e almeno uno uguale a 0:

$\lambda \leq 0$

La matrice Hessiana è definita negativa se tutti i suoi autovalori (o autovalori) sono minori di 0 (negativi):

$\lambda < 0$

La matrice Hessiana è indefinita quando ha autovalori (o autovalori) positivi e negativi:

$\lambda > 0 \qquad \lambda <0$

Criterio di Silvestro

Un altro modo per sapere di che tipo è la matrice assiana è utilizzare il criterio di Sylvester, anche se questo teorema ci permette solo di sapere se è definita positiva, definita negativa o indefinita. Ma a volte può essere molto più veloce da usare perché i calcoli sono generalmente più semplici.

Pertanto, il criterio di Sylvester è il seguente:

Se tutti i minori principali della matrice assiana sono maggiori di 0, si tratta di una matrice definita positiva .

Se i minori principali della matrice Hessiana con indice pari sono maggiori di 0 e quelli con indice dispari sono minori di 0, si tratta di una matrice definita negativa .

Se tutti i minori principali della matrice assiana sono diversi da 0 e nessuna delle due condizioni precedenti è soddisfatta, si tratta di una matrice indefinita .

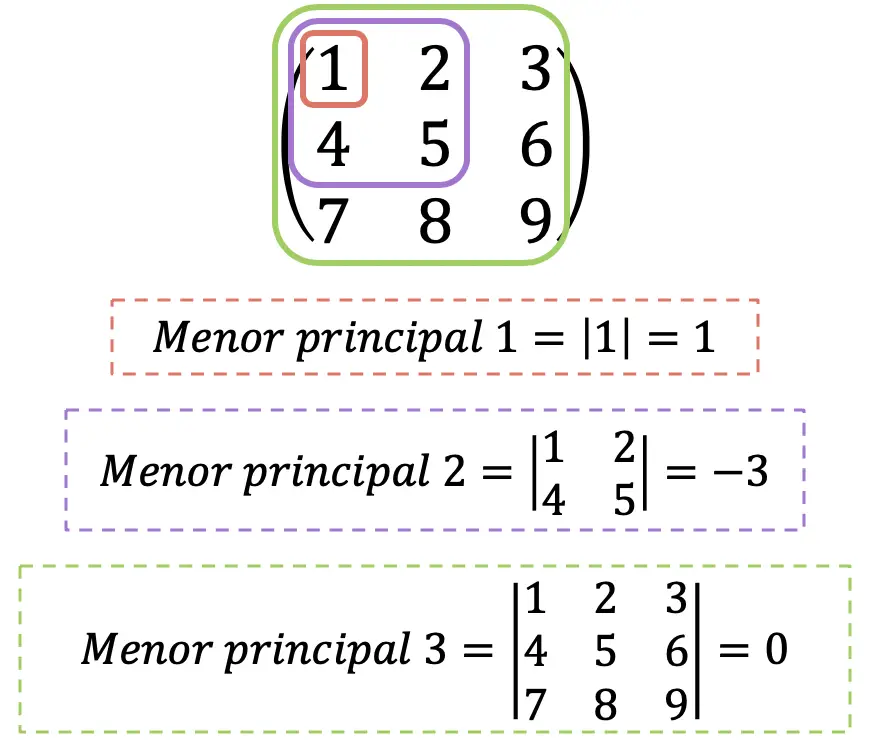
Ovviamente il massimo principale minore della matrice Hessiana coinciderà sempre con il suo determinante. Solo a scopo informativo, il determinante della matrice dell’Assia è anche chiamato “l’Assia”, anche se non lo faremo qui per evitare confusione.

Come calcolare il massimo o il minimo di una funzione con la matrice Hessiana

Una volta che sai come calcolare la matrice dell’Assia, probabilmente ti starai chiedendo: e a cosa serve questa matrice?

Ebbene, una delle applicazioni della matrice Hessiana è trovare il massimo o il minimo di una funzione con più di una variabile. Ecco una spiegazione passo passo su come calcolare i massimi e i minimi:

Innanzitutto vengono calcolati i punti critici della funzione multivariabile. Per fare ciò, calcoliamo il gradiente o la matrice Jacobiana della funzione, impostiamolo uguale a 0 e risolviamo le equazioni.
Viene calcolata la matrice dell’Assia.
I punti critici trovati nel passaggio 1 vengono sostituiti nella matrice dell’Assia. Otterremo così tante matrici Hessiane quanti sono i punti critici che hanno la funzione.
Vediamo che tipo di matrice è ciascuna matrice dell’Assia. Osserviamo cioè se è definito positivo, definito negativo, indefinito, ecc.
- Se la matrice Hessiana è definita positiva, il punto critico è un minimo relativo della funzione.
- Se la matrice Hessiana è definita negativa, il punto critico è un massimo relativo della funzione.
- Se la matrice Hessiana non è definita, il punto critico è un punto di sella .

Esempio di calcolo dei massimi e dei minimi di una funzione multivariabile

Per vedere come viene fatto, ecco un esempio di calcolo e classificazione degli estremi relativi di una funzione utilizzando la matrice Hessiana:

Trova tutti gli estremi relativi della seguente funzione multivariabile:

$\displaystyle f(x,y)=x^2-y^2+2xy+ 4x-4y$

La prima cosa che dobbiamo fare è calcolare la matrice Jacobiana della funzione, che in questo caso coinciderà con il gradiente perché è una funzione scalare:

$\displaystyle \nabla f (x,y)=(2x+2y+4 \ , \ -2y+2x-4 )$

Dobbiamo ora determinare i punti critici, per fare questo uguagliamo a 0 le equazioni ottenute e risolviamo il sistema di equazioni:

$\displaystyle \nabla f (x,y)=0$

$\displaystyle \left. \begin{array}{l} 2x+2y+4 =0 \\[2ex] -2y+2x-4=0 \end{array}\right\} \longrightarrow \left. \begin{array}{c} x = 0 \\[1.1ex] y = -2 \end{array}\right\} \longrightarrow \ (0,-2)$

Quindi il punto critico che abbiamo trovato è (0,-2).

Trovato il punto critico della funzione, dobbiamo calcolare la matrice Hessiana:

$\displaystyle H_f (x,y)=\begin{pmatrix}2 & 2 \\[1.1ex] 2 & -2 \end{pmatrix}$

E, ovviamente, la matrice Hessiana valutata nel punto critico è la stessa:

$\displaystyle H_f (0,-2)=\begin{pmatrix}2 & 2 \\[1.1ex] 2 & -2 \end{pmatrix}$

Per vedere di che tipo di matrice si tratta, utilizzeremo il criterio di Sylvester. Risolviamo quindi i minori principali della matrice:

$\displaystyle \begin{vmatrix}2 \end{vmatrix} = 2$

$\displaystyle \begin{vmatrix}2 & 2 \\[1.1ex] 2 & -2 \end{vmatrix} = -8$

La principale minore 1 (dispari) è positiva e la principale minore 2 (pari) è negativa, quindi secondo il criterio di Sylvester è una matrice indefinita. E, quindi, il punto critico (0,-2) è un punto di sella.

Determinazione della concavità o convessità di una funzione con la matrice Hessiana

Un altro utilizzo della matrice Hessiana è sapere se una funzione è concava o convessa. E questo può essere determinato secondo il seguente teorema:

Essere

$A \subseteq \mathbb{R}^n$

un insieme aperto e

$f \colon A \to \mathbb{R}$

una funzione le cui derivate seconde sono continue, la sua concavità e convessità sono definite dalla matrice Hessiana:

Funzione
$f$

è convesso ovunque

$A$

se e solo se la sua matrice Hessiana è semidefinita positiva in ogni punto dell’insieme.
Funzione
$f$

è rigorosamente convesso ovunque

$A$

se e solo se la sua matrice Hessiana è definita positiva in ogni punto dell’insieme.

✓ Pertanto, se

$f$

è una funzione convessa in un punto in cui anche la matrice Jacobiana svanisce, questo punto è un minimo locale .

Funzione
$f$

è complessivamente concavo

$A$

se e solo se la sua matrice Hessiana è semidefinita negativa in ogni punto dell’insieme.
Funzione
$f$

è complessivamente rigorosamente concavo

$A$

se e solo se la sua matrice Hessiana è definita negativa in ogni punto dell’insieme.

✓ Pertanto, se

$f$

è una funzione concava in un punto in cui anche la matrice Jacobiana svanisce, questo punto è un massimo locale .

Di seguito hai un esempio di funzione convessa e un altro di funzione concava rappresentata in uno spazio tridimensionale:

funzione convessa

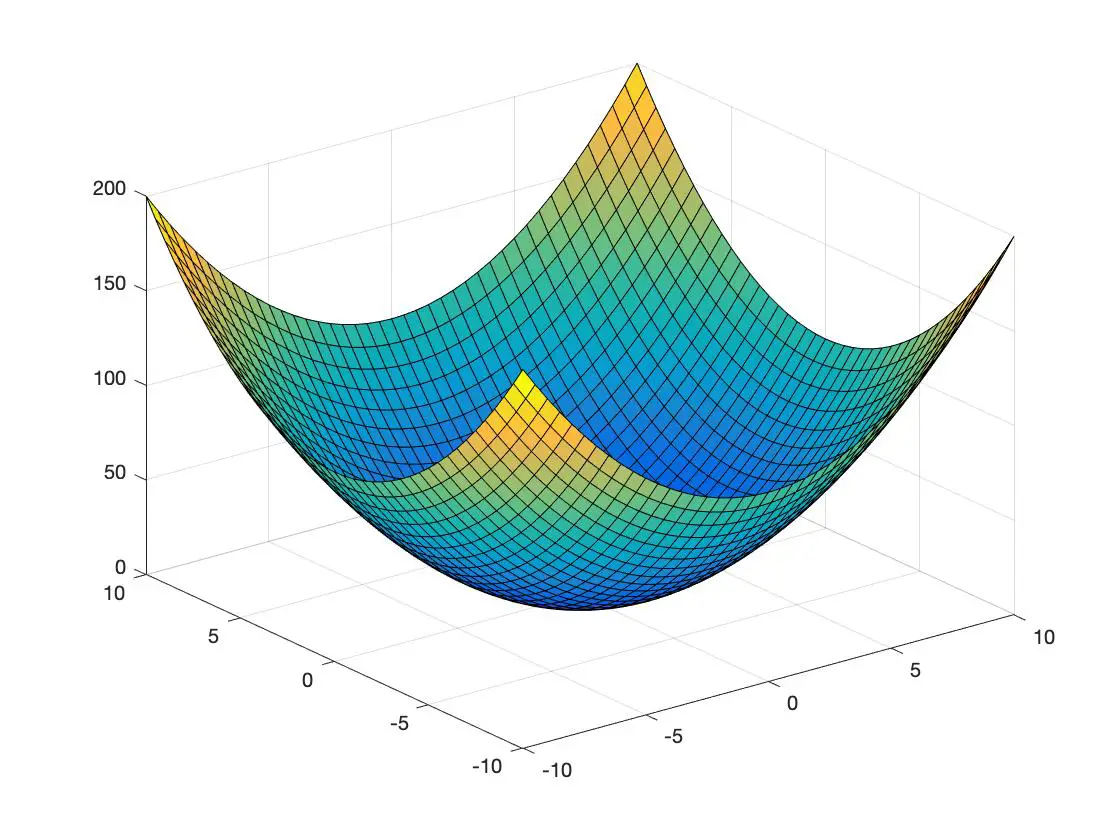
funzione concava

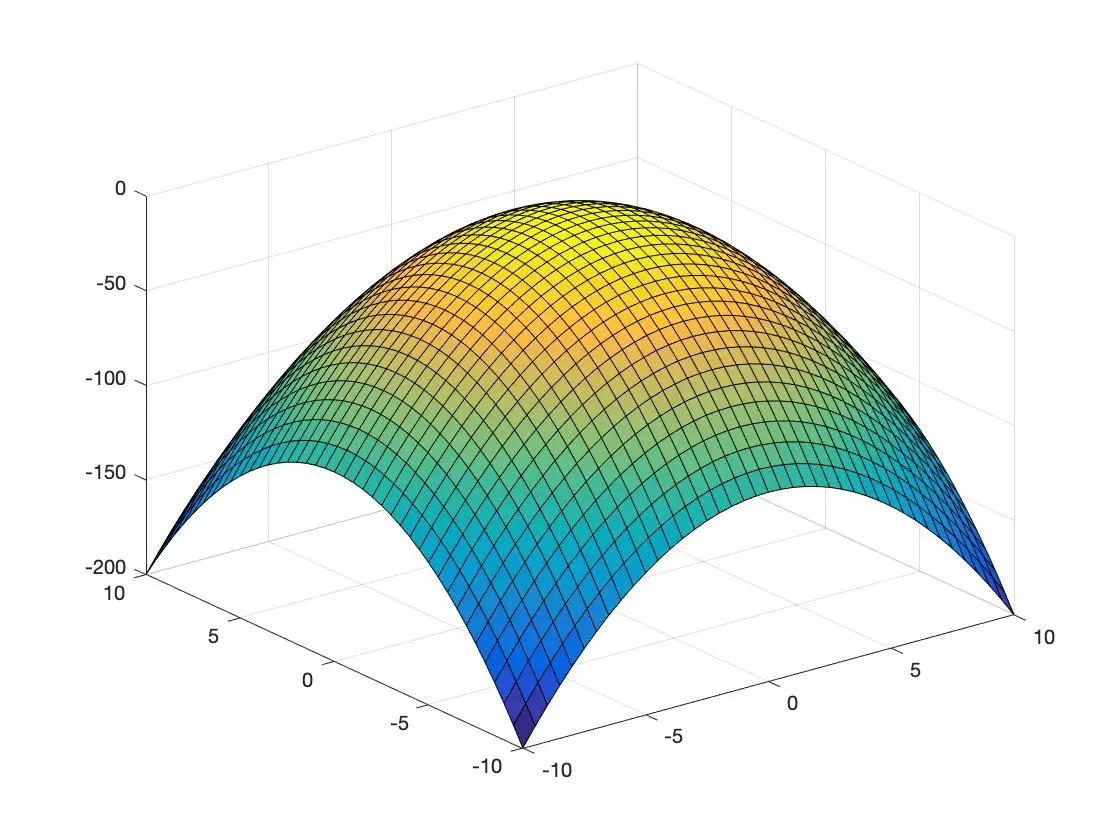
L'immagine ha un attributo ALT vuoto; il nome del file è concavità-e-convessità-di-una-funzione-con-la-matrice-di-iuta-1024x768.jpg

Ulteriori applicazioni della matrice dell’Assia

Gli usi principali della matrice Hessiana sono quelli che abbiamo già visto, tuttavia ha anche altre applicazioni. Ve li spieghiamo di seguito per i più curiosi.

Polinomio di Taylor

L’espansione del polinomio di Taylor per funzioni di 2 o più variabili nel punto

$a$

inizia così:

$\displaystyle T(x) = f(a) + (x-a)^T \nabla f(a) + \frac{1}{2}(x-a)^T \operatorname{H}_f(a)(x-a) + \ldots$

Come puoi vedere, i termini del secondo ordine dell’espansione di Taylor sono dati dalla matrice Hessiana valutata nel punto di espansione del polinomio.

Matrice di tela bordata

Un altro utilizzo della matrice Hessiana è calcolare i minimi e i massimi di una funzione multivariata

$f(x,y)$

limitato a un altro ruolo

$g(x,y)$

. Per risolvere questo problema si utilizza la matrice Hessiana limitata e si segue la seguente procedura:

Passaggio 1: viene calcolata la funzione Lagrange, definita dalla seguente espressione:

$\displaystyle L(x,y,\lambda) = f(x,y)+ \lambda \cdot g(x,y)$

Passo 2: Vengono trovati i punti critici della funzione Lagrange. Per fare ciò, calcoliamo il gradiente della funzione di Lagrange, impostiamo le equazioni uguali a 0 e risolviamo le equazioni.

$\displaystyle \nabla L = 0$

$\displaystyle \cfrac{\partial L}{\partial x} = 0 \qquad \cfrac{\partial L}{\partial y}=0 \qquad \cfrac{\partial L}{\partial \lambda}=0$

Passaggio 3: Per ogni punto trovato, calcoliamo l’Assia delimitata, che è definita dalla seguente matrice:

$\displaystyle H(f,g) = \begin{pmatrix}0 & \cfrac{\partial g}{\partial x_1} & \cfrac{\partial g}{\partial x_2} & \cdots & \cfrac{\partial g}{\partial x_n} \\[4ex] \cfrac{\partial g}{\partial x_1} & \cfrac{\partial^2 f}{\partial x_1^2} & \cfrac{\partial^2 f}{\partial x_1\,\partial x_2} & \cdots & \cfrac{\partial^2 f}{\partial x_1\,\partial x_n} \\[4ex] \cfrac{\partial g}{\partial x_2} & \cfrac{\partial^2 f}{\partial x_2\,\partial x_1} & \cfrac{\partial^2 f}{\partial x_2^2} & \cdots & \cfrac{\partial^2 f}{\partial x_2\,\partial x_n} \\[3ex] \vdots & \vdots & \vdots & \ddots & \vdots \\[3ex] \cfrac{\partial g}{\partial x_n} & \cfrac{\partial^2 f}{\partial x_n\,\partial x_1} & \cfrac{\partial^2 f}{\partial x_n\,\partial x_2} & \cdots & \cfrac{\partial^2 f}{\partial x_n^2}\end{pmatrix}$

Passaggio 4: determiniamo per ciascun punto critico se è un massimo o un minimo:

Questo sarà un massimo locale della funzione
$f$

sotto vincoli di funzione

$g$

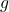
se gli ultimi nm (dove n è il numero di variabili e m il numero di vincoli) principali minori della matrice Hessiana delimitata valutata nel punto critico hanno segni alternati iniziando dal segno negativo.

Questo sarà un minimo locale della funzione
$f$

sotto vincoli di funzione

$g$

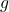
se gli ultimi nm (dove n è il numero di variabili e m il numero di vincoli) principali minori della matrice Hessiana netta valutata nel punto critico hanno tutti segno negativo.

Va tenuto presente che i minimi o massimi relativi di una funzione vincolata rispetto a un’altra non devono necessariamente essere così per la funzione non vincolata. La matrice Hessiana delimitata è quindi utile solo per questo tipo di problemi.

Rapporto con altre operazioni

Infine, la matrice Hessiana è legata anche ad altre importanti operazioni o matrici, principalmente con la matrice Jacobiana e con l’operatore di Laplace.

Relazione con la matrice Jacobiana

La matrice Hessiana di una funzione

$f$

è la matrice Jacobiana del gradiente della stessa funzione:

$\displaystyle H_f = J(\nabla f)$

Operatore di Laplace

La traccia della matrice Hessiana è equivalente all’operatore di Laplace :

$\displaystyle tr( H_f) = \Delta f$

Questa uguaglianza può essere facilmente dimostrata, poiché la definizione dell’operatore di Laplace è la divergenza del gradiente di una funzione:

$\displaystyle \Delta f =\nabla \cdot (\nabla f) = (\nabla \cdot \nabla )f = \nabla^2 f$

La sua espressione è quindi:

$\displaystyle \Delta f = \cfrac{\partial ^2 f}{\partial^2 x_1} +\cfrac{\partial ^2 f}{\partial^2 x_2} + \cfrac{\partial ^2 f}{\partial^2 x_3}+ \ldots +\cfrac{\partial ^2 f}{\partial^2 x_n}$

E questa somma è solo la traccia della matrice assiana, quindi l’equivalenza è dimostrata.

Matrice dell'assia (o hesse)

Cos’è la matrice dell’Assia?

Esempio di calcolo della matrice Hessiana

Problemi risolti delle matrici Hessiane

Esercizio 1

Esercizio 2

Esercizio 3

Esercizio 4

Come fai a sapere quando la matrice dell’Assia è positiva, negativa o indefinita?

Criterio degli autovalori (o autovalori)

Criterio di Silvestro

Come calcolare il massimo o il minimo di una funzione con la matrice Hessiana

Esempio di calcolo dei massimi e dei minimi di una funzione multivariabile

Determinazione della concavità o convessità di una funzione con la matrice Hessiana

Ulteriori applicazioni della matrice dell’Assia

Polinomio di Taylor

Matrice di tela bordata

Rapporto con altre operazioni

Relazione con la matrice Jacobiana

Operatore di Laplace

Lascia un commento Annulla risposta