Matrice antihermitiana (o antihermitiana).

In questa pagina vedrai cos’è una matrice antihermitiana, detta anche matrice antihermitiana. Troverai esempi di matrici anti-Hermitiane, tutte le loro proprietà e la forma di questo tipo di matrici quadrate complesse. Infine, troverai la spiegazione di come scomporre qualsiasi matrice complessa nella somma di una matrice anti-Hermitiana più un’altra matrice Hermitiana.

Cos’è una matrice antihermitiana o antihermitiana?

Una matrice anti-Hermitiana , o detta anche matrice anti-Hermitiana, è una matrice quadrata di numeri complessi la cui trasposizione coniugata è uguale alla stessa matrice ma di segno diverso.

A^*=-A

Oro

A^*

è la matrice coniugata trasposta di

A

.

Per curiosità, questo tipo di matrice è chiamata così perché soddisfa la condizione opposta della matrice hermitiana , il cui nome deriva dall’importante matematico francese Charles Hermite, professore e ricercatore di matematica del XIX secolo che compì importanti studi tra cui in il campo dell’algebra lineare.

Esempi di matrici antihermitiane

Una volta vista la definizione di matrice antihermitiana (o matrice antihermitiana) vedremo alcuni esempi di matrici antihermitiane di diverse dimensioni:

Esempio di matrice antihermitiana di ordine 2×2

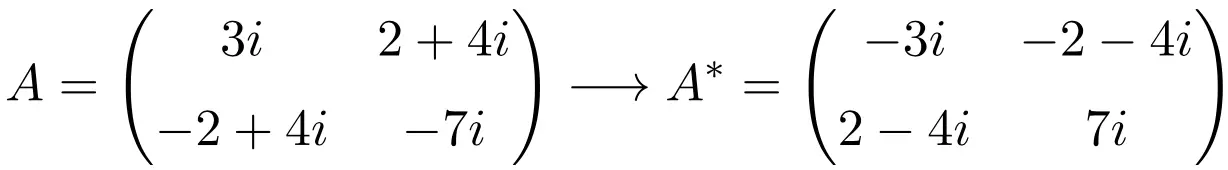
matrice antihermitiana o antihermitiana di dimensione 2x2

Esempio di matrice antihermitiana di dimensione 3×3

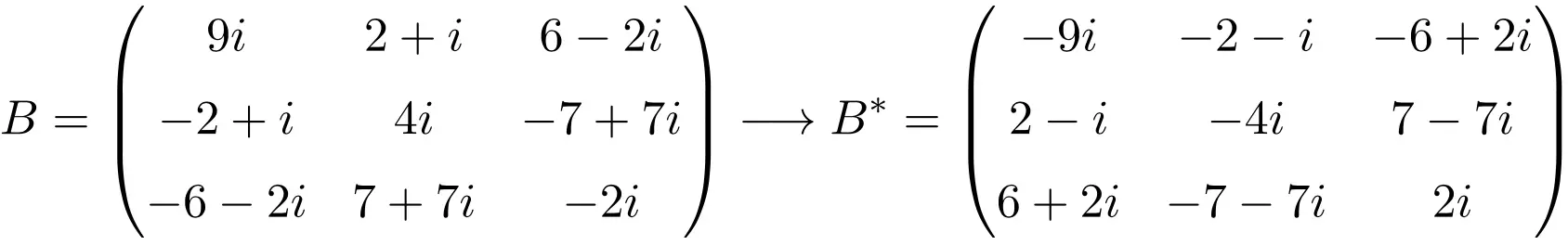
matrice antihermitiana o antihermitiana di dimensione 3x3

Esempio di matrice antihermitiana di dimensione 4×4

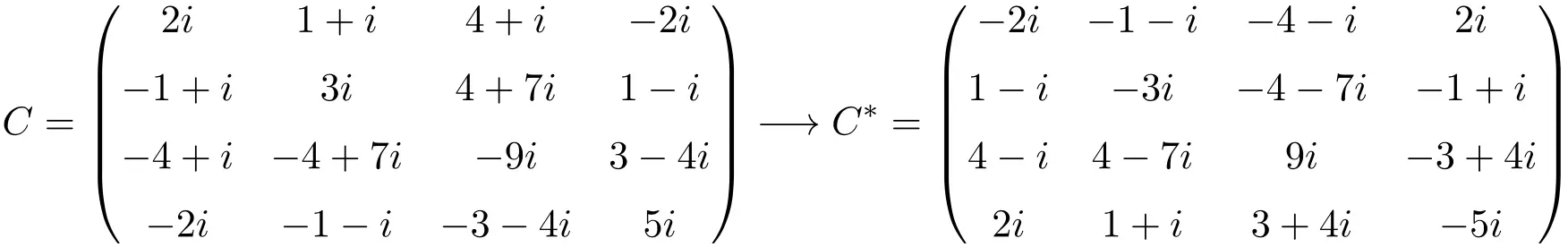
matrice antihermitiana o antihermitiana di dimensione 4x4

Come puoi vedere, le matrici A, B e C sono anti-Hermitiane perché la matrice trasposta coniugata di ciascuna è uguale alla matrice stessa ma con tutti gli elementi cambiati segno.

Struttura di una matrice antihermitiana

Se avete già visto gli esempi precedenti, le matrici anti-Hermitiane hanno sempre la stessa struttura: sono formate dai numeri immaginari (privi di parte reale) sulla diagonale principale, e dall’elemento complesso situato sulla i-esima retta e sulla j-esima linea. la colonna deve avere la stessa parte immaginaria e la stessa parte reale ma cambiato segno come l’elemento della j-esima riga e della i-esima colonna.

Anche se questo può sembrare un po’ complicato, è sicuramente meglio compreso dal seguente esempio:

Struttura di una matrice antihermitiana di dimensione 2×2

\displaystyle \begin{pmatrix} ai & b+ci\\[1.1ex]-b+ci & di \end{pmatrix}

Come puoi vedere, gli elementi della diagonale principale di una matrice antihermitiana sono totalmente immaginari e gli elementi della diagonale secondaria hanno la stessa parte immaginaria e la parte reale ha cambiato segno.

Pertanto, la parte reale di una matrice antihermitiana deve essere antisimmetrica e la parte immaginaria simmetrica.

Proprietà della matrice antihermitiana

Vedremo ora quali sono le proprietà di questo tipo di matrice quadrata complessa:

  • Ogni matrice antihermitiana è un esempio di matrice normale . Sebbene non tutte le matrici normali siano matrici antiermitiche.
  • Qualsiasi matrice anti-Hermitiana è diagonalizzabile. Inoltre, la matrice diagonale risultante contiene solo elementi puramente immaginari.
  • Pertanto gli autovalori (o autovalori) di una matrice anti-Hermitiana sono sempre numeri immaginari.
  • Allo stesso modo, gli autovettori (o autovettori) di diversi autovalori di una matrice anti-Hermitiana sono ortogonali.
  • Una matrice di numeri reali, vale a dire che nessun elemento ha una parte immaginaria, è antihermitiana se e solo se è una matrice antisimmetrica .
  • Una matrice antihermitiana può essere espressa come la somma di una matrice antisimmetrica reale e di una matrice simmetrica immaginaria.

A =B+Ci

  • La somma (o sottrazione) di due matrici anti-Hermitiane è uguale a un’altra matrice anti-Hermitiana.
  • Il risultato del prodotto di una matrice anti-Hermitiana e uno scalare è un’altra matrice anti-Hermitiana se lo scalare è un numero reale.
  • La potenza di una matrice anti-Hermitiana è pari a una matrice anti-Hermitiana se l’esponente è dispari; se invece viene elevato ad un esponente pari il risultato sarà una matrice hermitiana.
  • Sì

    A

    è una matrice antihermitiana, allora il prodotto

    iA

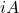
    è una matrice hermitiana.

Scomposizione di una matrice complessa in una matrice anti-Hermitiana e una matrice Hermitiana

Qualsiasi matrice contenente numeri complessi può essere scomposta nella somma di una matrice anti-Hermitiana più un’altra matrice Hermitiana . Ma per questo è necessario conoscere le seguenti caratteristiche di questi tipi di matrici:

  • La somma di una matrice quadrata complessa più il suo coniugato trasposto è equivalente a una matrice hermitiana (o hermitiana):

C + C^* = \text{Matriz Hermitiana}

  • La differenza tra una matrice quadrata complessa e il suo coniugato trasposto è uguale a una matrice anti-Hermitiana:

C - C^* = \text{Matriz Antihermitiana}

  • Pertanto, tutte le matrici complesse possono essere scomposte nella somma di una matrice Hermitiana e di una matrice anti-Hermitiana. Questo teorema è noto come decomposizione di Teoplitz :

\displaystyle \begin{array}{c} C = A + B \\[2ex] A = \cfrac{1}{2}\cdot (C+C^*) \qquad B = \cfrac{1}{2} \cdot (C-C^*)\end{array}

Dove C è la matrice complessa che vogliamo scomporre, C* il suo coniugato trasposto, ed infine A e B sono rispettivamente le matrici Hermitiana e AntiHermitiana in cui viene scomposta la matrice C.

Lascia un commento

Il tuo indirizzo email non sarà pubblicato. I campi obbligatori sono contrassegnati *

Torna in alto