Limiti laterali - Mathority

In questo articolo spieghiamo cos’è il limite laterale di una funzione (con esempi). Ti insegniamo anche come calcolare i limiti laterali sinistro e destro di una funzione, sia graficamente che numericamente. Inoltre, potrai allenarti con esercizi risolti passo dopo passo sui limiti laterali.

Quali sono i limiti laterali?

I limiti laterali di una funzione in un punto studiano il comportamento della funzione attorno a quel punto. Esiste il limite laterale sinistro e il limite laterale destro, che analizza il valore della funzione rispettivamente a sinistra e a destra del punto considerato.

Limiti laterali sinistro e destro

Come abbiamo visto nella definizione di confini laterali, esistono due tipologie: confini laterali sinistri e confini laterali destri.

Il limite sinistro della funzione è espresso con un segno meno nel punto in cui si analizza il limite e, invece, il limite destro è indicato con il segno più.

Limite laterale a sinistra

$\displaystyle\lim_{x\to a^{\color{orange}\bm{-}\color{black}}}f(x)$

Limite laterale a destra

$\displaystyle\lim_{x\to a^{\color{orange}\bm{+}\color{black}}}f(x)$

Guarda il seguente esempio per comprendere meglio il significato dei limiti laterali:

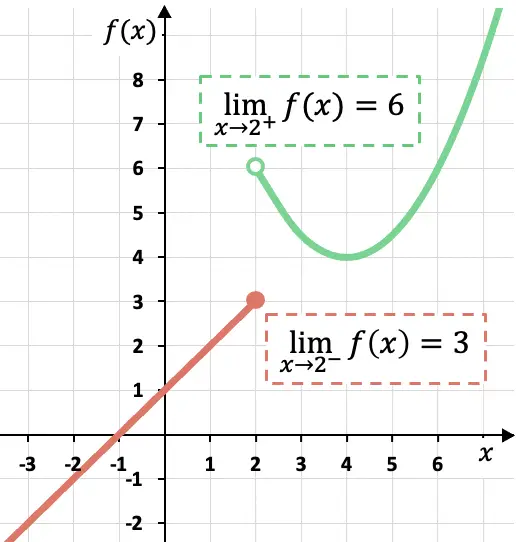
Come puoi vedere nella rappresentazione grafica di questa funzione a tratti, i limiti laterali dipendono dal lato su cui vengono calcolati.

In questo caso, la funzione si avvicina a 3 quando x si avvicina a 2 da sinistra, poiché la funzione assume valori più vicini a 3 quando x si avvicina a x=2 da sinistra.

Invece il limite laterale della funzione in x=2 tramite la retta vale 6. Perché se ci avviciniamo al punto x=2 tramite la sua retta, la funzione assume valori sempre più vicini a f(x)= 6.

D’altra parte, dovresti sapere che i limiti laterali hanno le stesse proprietà dei limiti ordinari. Nel seguente link puoi vedere quali sono le proprietà del confine:

➤ Vedi: proprietà del confine

limiti laterali uguali

Abbiamo appena visto un esempio in cui i limiti laterali di una funzione sono diversi, ma… cosa succede se i limiti laterali sono gli stessi?

Se entrambi i limiti laterali di una funzione in un punto esistono e sono uguali , il limite della funzione esiste in quel punto e il risultato del limite è il valore dei limiti laterali.

In altre parole, affinché esista il limite di una funzione in un punto, deve essere soddisfatta la seguente condizione:

$\displaystyle\lim_{x\to a^-}f(x)=\lim_{x\to a^+}f(x)=L \ \iff \ \lim_{x\to a}f(x)=L$

Pertanto, se i limiti laterali di una funzione in un punto sono diversi, il limite della funzione in quel punto non esiste.

Inoltre, che esista il limite di una funzione in un punto è una condizione essenziale affinché essa sia una funzione continua in un punto .

Risolviamo un esempio per completare la comprensione del concetto di limiti laterali:

I limiti laterali nel punto x=-2 della funzione rappresentata graficamente coincidono, poiché il valore della funzione tende a 3 sia che ci si avvicini a x=-2 da sinistra che da destra. Pertanto il limite della funzione in x=-2 è pari a 3.

$\displaystyle\lim_{x\to -2^-}f(x)=\lim_{x\to -2^+}f(x)=3 \ \longrightarrow \ \lim_{x\to -2}f(x)=3$

Nel punto x=4 invece i limiti laterali sono diversi, poiché da sinistra la funzione si avvicina a f(x)=3 ma da destra la funzione si avvicina a f(x)=2. Il limite della funzione a questo punto quindi non esiste.

$\displaystyle\lim_{x\to 4^-}f(x)=3 \neq \lim_{x\to 4^+}f(x)=2 \ \longrightarrow \ \cancel{\exists} \ \lim_{x\to 4}f(x)$

Calcolo dei limiti laterali

Data la definizione di limiti laterali, vedremo come vengono calcolati numericamente risolvendo il seguente esempio:

$\displaystyle\lim_{x\to 2}\frac{3}{x-2}$

Se calcoliamo il limite come al solito, otteniamo l’indeterminatezza di un numero reale diviso per 0:

$\displaystyle\lim_{x\to 2}\frac{3}{x-2}=\frac{3}{2-2}=\frac{3}{0}=\infty$

Tuttavia, quando si calcolano i limiti laterali, non si ottiene alcuna indeterminazione.

$\displaystyle\lim_{x\to 2^-}\frac{3}{x-2}=\ \color{red}\bm{?}\color{black} \qquad \lim_{x\to 2^+}\frac{3}{x-2}=\ \color{red}\bm{?}$

Per calcolare il limite laterale della funzione da sinistra in x=2, devi prendere un numero minore di x=2 ma molto vicino ad esso, ad esempio x=1.999.

$\displaystyle\lim_{x\to 2^-}\frac{3}{x-2}=\frac{3}{\color{red}\bm{1,999}\color{black}-2}$

In questo caso il denominatore sarà un numero negativo con un valore molto piccolo ma nemmeno zero, e solitamente è rappresentato da uno zero e da un segno meno davanti:

$\displaystyle\lim_{x\to 2^-}\frac{3}{x-2}=\frac{3}{1,999-2}=\frac{3}{\color{red}\bm{-0}\color{black}}$

Pertanto, il risultato del limite laterale è meno infinito, perché qualsiasi numero diviso per 0 dà infinito, e positivo diviso per negativo dà negativo:

$\displaystyle\lim_{x\to 2^-}\frac{3}{x-2}=\frac{3}{1,999-2}=\frac{3}{-0}=\color{red}\bm{-\infty}\color{black}$

Possiamo verificare che la funzione si avvicina a meno infinito calcolando le immagini della funzione con valori più vicini a x=2 da sinistra.

$\begin{array}{c}\begin{array}{l}f(1,9)=\cfrac{3}{1,9-2}=-30\\[2ex]f(1,99)=\cfrac{3}{1,99-2}=-300\\[2ex]f(1,999)=\cfrac{3}{1,999-2}=-3000\\[2ex]f(1,9999)=\cfrac{3}{1,9999-2}=-30000\\[2ex]f(1,99999)=\cfrac{3}{1,99999-2}=-300000\end{array}\\[16ex]\vdots\\[1.5ex] f(2^-)=-\infty\end{array}$

Allo stesso modo, per trovare il limite della funzione nel punto x=2 a destra, possiamo applicare lo stesso ragionamento: prendiamo un valore maggiore di 2 ma molto vicino, come 2001.

$\displaystyle\lim_{x\to 2^+}\frac{3}{x-2}=\frac{3}{2,001-2}=\frac{3}{+0}=+\infty$

Allo stesso modo possiamo verificare che la funzione tende all’infinito calcolando immagini della funzione con valori sempre più vicini a x=2 da destra.

$\begin{array}{c}\begin{array}{l}f(2,1)=\cfrac{3}{2,1-2}=30\\[2ex]f(2,01)=\cfrac{3}{2,01-2}=300\\[2ex]f(2,001)=\cfrac{3}{2,001-2}=3000\\[2ex]f(2,0001)=\cfrac{3}{2,0001-2}=30000\\[2ex]f(2,00001)=\cfrac{3}{2,00001-2}=300000\end{array}\\[16ex]\vdots\\[1.5ex] f(2^+)=+\infty\end{array}$

Nel grafico seguente potete vedere rappresentata la funzione analizzata. Come puoi vedere, il limite laterale della funzione nel punto x=2 a sinistra è meno infinito, e il limite laterale della funzione nel punto x=2 a destra è più infinito.

Risolti i problemi relativi ai confini laterali

Esercizio 1

Trova i limiti laterali della seguente funzione definita a tratti nei punti in cui cambia la definizione (x=-2 e x=4).

vedi soluzione

I limiti laterali non coincidono nel punto x=-2, a sinistra la funzione tende verso f(x)=5 e, invece, a destra la funzione è costante e vale 3.

$\displaystyle\lim_{x\to -2^-}f(x)=5$

$\displaystyle\lim_{x\to -2^+}f(x)=3$

Anche i limiti laterali sono diversi quando x si avvicina a 4. La funzione a tratti si avvicina a 3 da sinistra, ma si avvicina a -2 da destra.

$\displaystyle\lim_{x\to 4^-}f(x)=3$

$\displaystyle\lim_{x\to 4^+}f(x)=-2$

Esercizio 2

Determina se il limite esiste quando x tende a 3 della seguente funzione a tratti e, in tal caso, qual è il suo valore.

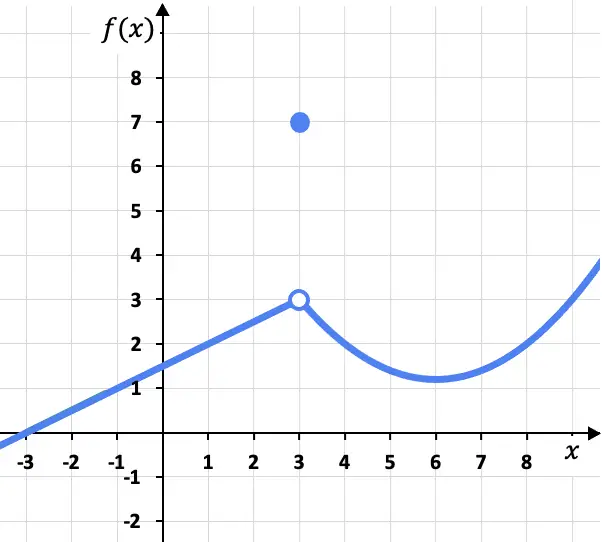
Limiti laterali di una funzione a tratti

vedi soluzione

In questo problema i limiti laterali nel punto x=3 da sinistra e da destra sono identici, poiché la funzione tende allo stesso valore (f(x)=3) sia che venga avvicinata da sinistra che da destra . il suo lato destro:

$\displaystyle\lim_{x\to 3^-}f(x)=3$

$\displaystyle\lim_{x\to 3^+}f(x)=3$

Pertanto, secondo la definizione matematica del limite, il limite della funzione quando x tende a 3 è uguale a 3, perché i due limiti laterali in questo stesso punto coincidono a questo valore:

$\displaystyle\lim_{x\to 3^-}f(x)=\lim_{x\to 3^+}f(x)=3 \ \longrightarrow \ \lim_{x\to 3}f(x)=3$

Sebbene il limite della funzione in x=3 sia 3, bisogna tenere conto che la funzione in questo punto non è 3, ma che f(3)=7. Come vedremo in seguito, ciò significa che la funzione non è continua in x=3, ma presenta piuttosto una discontinuità evitabile.

Esercizio 3

Calcola i limiti laterali della seguente funzione razionale nel punto x=4.

$f(x)=\cfrac{-2x+3}{x-4}$

vedi soluzione

Per calcolare il limite quando x tende a 4 da sinistra, prendiamo un valore inferiore a 4 ma molto vicino ad esso, ad esempio 3.999:

$\displaystyle\lim_{x\to 4^-}\frac{-2x+3}{x-4}=\frac{-2\cdot 3,999+3}{3,999-4}=\frac{-4,998}{-0}=+\infty$

Quindi il limite laterale per x che si avvicina a 4 da sinistra è più infinito.

E per risolvere il limite quando x tende a 4 da destra, valutiamo la funzione ad un valore maggiore di 4 ma molto vicino ad esso, ad esempio 4.001:

$\displaystyle\lim_{x\to 4^+}\frac{-2x+3}{x-4}=\frac{-2\cdot 4,001+3}{4,001-4}=\frac{-5,002}{+0}=-\infty$

Quindi il limite laterale per x che si avvicina a 4 da destra è meno infinito.

Esercizio 4

Trovare il limite, se esiste, della seguente funzione a tratti definita nel punto x=2:

$\displaystyle f(x)= \left\{ \begin{array}{lcl} x^2-3 & \text{si} & x \leq 2 \\[2ex]\displaystyle \frac{-3x+5}{x-3} & \text{si} & x>2 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”75″ width=”235″ style=”vertical-align: 0px;”></p> </p> <div class=$

vedi soluzione

In questo caso, la formulazione del problema ci chiede di trovare il limite in cui la funzione a tratti cambia espressione, quindi dobbiamo trovare il limite a sinistra utilizzando la prima espressione e il limite a destra utilizzando la seconda espressione.

$\displaystyle\lim_{x\to 2^+}f(x)=\lim_{x\to 2^+}\frac{-3x+5}{x-3}=\frac{-3\cdot 2+5}{2-3}=\frac{-1}{-1}=1$

Il limite della funzione in x=2 a sinistra coincide con il limite della funzione a destra, quindi il limite della funzione esiste ed è uguale a 1:

$\displaystyle\lim_{x\to 2^-}f(x)=\lim_{x\to 2^+}f(x)=1 \ \longrightarrow \ \lim_{x\to 2}f(x)=1$

Quali sono i limiti laterali?

Limiti laterali sinistro e destro

limiti laterali uguali

Calcolo dei limiti laterali

Risolti i problemi relativi ai confini laterali

Esercizio 1

Esercizio 2

Esercizio 3

Esercizio 4

Lascia un commento Annulla risposta