▷ Come risolvere i limiti all'infinito (+25 esercizi risolti)

Qui troverai come risolvere tutti i tipi di limiti all’infinito: funzioni polinomiali, razionali, esponenziali, con radici, indeterminazioni all’infinito… Inoltre, potrai allenarti con 25 esercizi risolti passo dopo passo sui limiti quando x tendere all’infinito. .

Limite di una funzione quando x tende all’infinito

Il limite di una funzione quando x si avvicina all’infinito , positivo o negativo, può essere un valore reale, più infinito, meno infinito o inesistente. Per risolvere i limiti all’infinito, è necessario sostituire x con infinito.

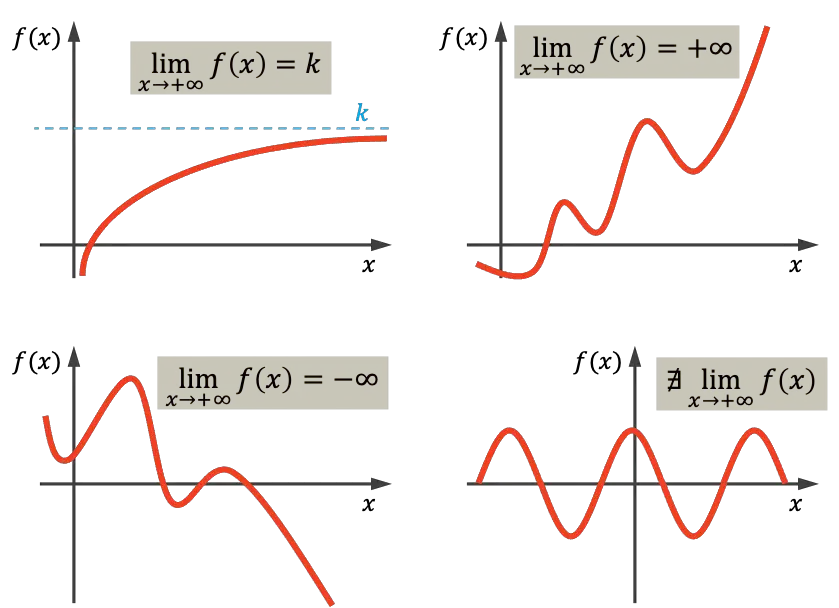
Come puoi vedere dal primo grafico, la funzione rappresentata tende al valore reale k verso l’infinito, perché si avvicina a k al crescere di x . La funzione in alto a destra tende all’infinito quando x si avvicina all’infinito, perché cresce indefinitamente all’aumentare del valore di x . Il grafico in basso a sinistra, invece, decresce senza fermarsi e tende quindi verso meno infinito. Infine, l’ultima funzione è periodica e non tende ad alcun valore, quindi in questo caso non c’è limite all’infinito.

Come risolvere i limiti all’infinito

Per risolvere un limite all’infinito nelle funzioni polinomiali, dobbiamo sostituire x con infinito solo nel termine di grado più alto della funzione.

Ad esempio, guarda il seguente calcolo di un limite all’infinito in cui sostituiamo solo l’infinito nel monomio di grado più alto:

$\displaystyle \lim_{x \to +\infty}(3x^2-4x+6) = 3(+\infty)^2 = \bm{+\infty}$

Come puoi vedere nell’esempio, +∞ al quadrato dà +∞, poiché un numero molto grande (+∞) elevato a 2 darà sempre un numero molto grande (+∞).

E la stessa cosa accade con la moltiplicazione: se moltiplichi un numero molto grande (+∞), otterrai sempre un numero molto grande (+∞). Per esempio:

$3\cdot (+\infty)= +\infty.$

Attenzione: per calcolare i limiti all’infinito è importante tenere conto dei seguenti elementi:

→ Un numero negativo elevato a un esponente pari è positivo. Pertanto meno infinito elevato ad esponente pari dà più infinito:

$(-\infty)^2 = +\infty$

→ Un numero negativo elevato a un esponente dispari è negativo. Pertanto, meno infinito elevato a un esponente dispari è meno infinito:

$(-\infty)^3 = -\infty$

→ Moltiplicando un numero negativo si cambia il segno dell’infinito:

$-2(+\infty) = - \infty$

→ Qualsiasi numero diviso per

$\pm \infty$

dà 0:

$\cfrac{5}{\infty} = 0$

Esempi di limiti all’infinito

Quindi puoi vedere come i limiti all’infinito vengono risolti nei polinomi, di seguito sono riportati diversi limiti risolti:

$\begin{array}{l}\displaystyle \lim_{x \to +\infty} (x^3-x^2+4)= (+\infty) ^3 = \bm{+\infty}\\[4ex]\displaystyle\lim_{x \to +\infty} (-5x+2)= -5(+\infty)= \bm{-\infty}\\[4ex]\displaystyle \lim_{x \to -\infty} (x^2-7x+1) = (-\infty)^2 = \bm{+\infty}\\[4ex]\displaystyle \lim_{x \to -\infty} (x^3-x^2+4)= (-\infty) ^3 = \bm{-\infty}\\[4ex]\displaystyle \lim_{x \to +\infty} \ \cfrac{1}{x}= \cfrac{1}{+\infty} = \bm{0}\end{array}$

Limiti indeterminati all’infinito

I limiti all’infinito non saranno sempre così facili da calcolare, poiché a volte otterremo l’indeterminazione dell’infinito tra infinito o l’indeterminazione dell’infinito meno infinito.

$\cfrac{\infty}{\infty}\qquad \qquad \infty-\infty$

Quando otteniamo questo tipo di indeterminazioni (o forme indeterminate), non possiamo conoscere direttamente il risultato, ma dobbiamo piuttosto eseguire una procedura preliminare per trovare il valore limite. Vedremo poi come si risolvono i limiti indeterminati all’infinito.

Infinita indeterminatezza tra gli infiniti

Per trovare il risultato dell’indeterminazione infinito diviso infinito dobbiamo confrontare il grado del numeratore e il grado del denominatore della frazione:

Se il grado del polinomio del numeratore è inferiore al grado del polinomio del denominatore, l’indeterminatezza infinita sull’infinito è uguale a zero.
Se il grado del polinomio del numeratore è equivalente al grado del polinomio del denominatore, l’indeterminatezza infinita su infinito è il quoziente dei coefficienti principali dei due polinomi.
Se il grado del polinomio del numeratore è maggiore del grado del polinomio del denominatore, l’infinita indeterminazione tra infinito dà più o meno infinito (il segno dipende dai termini principali dei due polinomi).

$\displaystyle \lim_{x \to \pm \infty}}\frac{a_nx^r+a_{n-1}x^{r-1}+a_{n-2}x^{r-2}+\dots}{b_nx^s+b_{n-1}x^{s-1}+b_{n-2}x^{s-2}+\dots}=\left\{ \begin{array}{lcl} 0 & \text{si} & r<s \\[3ex]="" \cfrac{a_n}{b_n}="" &="" \text{si}="" r="s" \\[5ex]="" \pm="" \infty="">s \end{array}\right.” title=”Rendered by QuickLaTeX.com” height=”139″ width=”767″ style=”vertical-align: 0px;”> Ad esempio, nel limite seguente, il polinomio del numeratore è di secondo grado, mentre il polinomio del denominatore è di terzo grado, quindi la soluzione del limite è 0. <p class=$ $\displaystyle \lim_{x \to +\infty} \cfrac{6x^2-5}{x^3+1} = \cfrac{6(+\infty)^2}{(+\infty)^3} = \cfrac{+\infty}{+\infty}= \bm{0}$

Guarda quest’altro esempio, in cui i due polinomi della funzione razionale sono di secondo grado, quindi dobbiamo dividere i coefficienti dei termini di grado superiore per calcolare il limite all’infinito.

$\displaystyle \lim_{x \to +\infty} \cfrac{4x^2+1}{2x^2-5} = \cfrac{4(+\infty)^2}{2(+\infty)^2}= \cfrac{+\infty}{+\infty} =\cfrac{4}{2} = \bm{2}$

Infine, al limite successivo, la funzione del numeratore ha grado maggiore di quella del denominatore, quindi l’indeterminazione di infinito su infinito dà infinito. Inoltre, dal numeratore si ottiene un infinito positivo, ma dal denominatore un infinito negativo, quindi il risultato del limite è negativo (il positivo tra i negativi è negativo).

$\displaystyle \lim_{x \to -\infty} \cfrac{3x^2+2x-5}{7x+1} = \cfrac{3(-\infty)^2}{7(-\infty)}=\cfrac{3(+\infty)}{-\infty}}= \cfrac{+\infty}{-\infty}= \bm{-\infty}$

Infinita indeterminatezza tra l’infinito con radici

Il grado di una funzione irrazionale (funzione con radici) è invece il quoziente tra il grado del termine principale e l’indice del radicale.

$\sqrt[\color{red}\bm{m}\color{black}]{a_nx^{\color{blue}\bm{n}\color{black}}+a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+\dots} \ \longrightarrow \ \text{grado}=\cfrac{\color{blue}\bm{n}\color{black}}{\color{red}\bm{m}\color{black}}$

Pertanto, se il limite di una funzione con radici dà infinita indeterminazione tra infinito , dobbiamo applicare le stesse regole spiegate sopra per quanto riguarda i gradi del numeratore e del denominatore, tenendo però conto che il grado di un polinomio con radici si calcola diversamente.

Guarda il seguente esempio del limite infinito di una funzione con radicali:

$\displaystyle\lim_{x\to +\infty}\frac{4x^2+11}{\sqrt{x^8-3x^2-5}}=\frac{4(+\infty)^2}{\sqrt{(+\infty)^8}}=\frac{+\infty}{+\infty}=\bm{0}$

Il grado del numeratore è 2 e il grado del denominatore è 4 (8/2=4), quindi il limite è 0 perché il grado del numeratore è inferiore al grado del denominatore.

Indeterminazione infinita tra infinito con funzioni esponenziali

La crescita di una funzione esponenziale è molto maggiore della crescita di una funzione polinomiale, quindi dobbiamo considerare che il grado di una funzione esponenziale è maggiore del grado di una funzione polinomiale.

$\text{exponencial}>\text{polinomio}” title=”Rendered by QuickLaTeX.com” height=”16″ width=”192″ style=”vertical-align: -4px;”> Quindi, se l’indeterminazione infinito diviso infinito risulta da un limite con funzioni esponenziali, dobbiamo semplicemente applicare le stesse regole che spiegano i gradi del numeratore e del denominatore, ma tenendo conto che una funzione esponenziale è di ordine superiore a un polinomio. Inoltre, se abbiamo funzioni esponenziali al numeratore e al denominatore della divisione, la funzione esponenziale con la base più grande sarà quella di ordine più alto. <p class=$ $\displaystyle\lim_{x\to +\infty}\frac{7x^5+6x^3-4x}{4^x}=\frac{7(+\infty)^5}{4^{+\infty}}=\frac{+\infty}{+\infty}=\bm{0}$

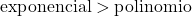
In questo esempio, il denominatore è formato da una funzione esponenziale, quindi è di ordine superiore rispetto al numeratore. Pertanto, la forma indeterminata infinito tra infinito dà 0.

Infinito meno infinita indeterminatezza

Risolvere l’infinito meno l’indeterminazione infinita dipende dal fatto che la funzione abbia frazioni o radici. Vediamo quindi come risolvere questo tipo di indeterminatezza per questi due diversi casi.

Indeterminazione infinito meno infinito con le frazioni

Quando si verifica l’indeterminazione infinito meno infinita in un’addizione o sottrazione di frazioni algebriche , dobbiamo prima eseguire l’addizione o la sottrazione delle frazioni e quindi calcolare il limite.

Vediamo come calcolare l’indeterminazione infinito meno infinito in una funzione con frazioni risolvendo passo dopo passo un esempio:

$\displaystyle \lim_{x \to +\infty} \left( \frac{x^2}{x-1} - \frac{x}{3}\right)$

Proviamo innanzitutto a calcolare il limite:

$\displaystyle \lim_{x \to +\infty}\left( \frac{x^2}{x-1} - \frac{x}{3}\right) = \frac{(+\infty)^2}{(+\infty)-1} - \frac{+\infty}{3} = \bm{+\infty - \infty}$

Ma otteniamo l’indeterminazione ∞-∞.

Dobbiamo prima sottrarre le frazioni. Per fare ciò, riduciamo le frazioni a un denominatore comune, ovvero moltiplichiamo il numeratore e il denominatore di una frazione per il denominatore dell’altra:

$\begin{array}{l}\displaystyle\lim_{x \to +\infty} \left( \frac{x^2}{x-1}-\frac{x}{3}\right)=\\[5ex]\displaystyle =\lim_{x \to +\infty}\left(\frac{x^2 \cdot 3}{(x-1)\cdot 3}- \frac{x\cdot (x-1)}{3\cdot (x-1)} \right)=\\[5ex]\displaystyle = \lim_{x \to +\infty} \left( \frac{3x^2 }{3(x-1)}- \frac{x^2-x}{3(x-1)}\right)\end{array}$

E ora che le due frazioni hanno lo stesso denominatore possiamo unirle in un’unica frazione:

$\displaystyle \lim_{x \to +\infty} \frac{3x^2 -(x^2-x)}{3(x-1)}$

Operiamo sul numeratore e sul denominatore:

$\displaystyle \lim_{x \to +\infty} \frac{3x^2 -x^2+x}{3x-3} = \lim_{x \to +\infty} \frac{2x^2+x}{3x-3}$

E infine calcoliamo nuovamente il limite:

$\displaystyle \lim_{x \to +\infty}\frac{2x^2+x}{3x-3}=\frac{+\infty}{+\infty}=\bm{+\infty}$

In questo caso l’infinita indeterminazione tra infinito dà +∞ perché il grado del numeratore è maggiore del grado del denominatore.

Indeterminazione infinito meno infinito con radici

Quando si verifica l’indeterminazione infinita meno infinita nell’addizione o nella sottrazione radicale , dobbiamo prima moltiplicare e dividere la funzione per l’espressione radicale coniugata e quindi risolvere il limite.

Vediamo come risolvere l’indeterminazione infinito meno infinito in una funzione irrazionale seguendo un esempio passo passo:

$\displaystyle\lim_{x\to +\infty}\left(x-\sqrt{x^2-5}\right)$

Proviamo innanzitutto a risolvere il limite della funzione con i radicali:

$\displaystyle\lim_{x\to +\infty}\left(x-\sqrt{x^2-5}\right)=+\infty-\sqrt{(+\infty)^2}=\bm{+\infty-\infty}$

Tuttavia, otteniamo la forma indeterminata ∞-∞. Quindi per sapere quanta indeterminazione fa infinito meno infinito devi applicare il procedimento spiegato.

Poiché la funzione ha radicali, moltiplichiamo e dividiamo l’intera funzione per l’espressione irrazionale coniugata:

$\displaystyle\lim_{x \to +\infty}\left(x-\sqrt{x^2-5}\right)= \lim_{x \to +\infty}\frac{\left(x-\sqrt{x^2-5}\right)\cdot\left(x+\sqrt{x^2-5}\right)}{x+\sqrt{x^2-5}}$

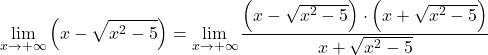
L’espressione algebrica del numeratore corrisponde all’identità notevole del prodotto di una somma e di una differenza, possiamo quindi semplificare l’espressione:

$\displaystyle \lim_{x \to +\infty} \cfrac{\left(x-\sqrt{x^2-5}\right) \cdot \left(x + \sqrt{x^2-5}\right)}{ x + \sqrt{x^2-5}}= \lim_{x \to +\infty} \cfrac{x^2- \left( \sqrt{x^2-5}\right)^2}{ x + \sqrt{x^2-5}}$

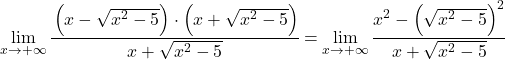
Ora semplifichiamo la radice del limite, poiché è quadrata:

$\displaystyle \lim_{x \to +\infty}\frac{x^2-(x^2-5)}{x+\sqrt{x^2-5}}$

Operiamo sul numeratore della frazione:

$\displaystyle \lim_{x \to +\infty} \frac{x^2- x^2+5}{x+\sqrt{x^2-5}}$

$\displaystyle \lim_{x \to +\infty} \frac{5}{x+\sqrt{x^2-5}}$

E infine, rifacciamo il calcolo del limite:

$\displaystyle \lim_{x \to +\infty} \frac{5}{x+\sqrt{x^2-5}}=\frac{5}{+\infty+\sqrt{(+\infty)^2}}=\frac{5}{+\infty}=\bm{0}$

Il risultato del limite è quindi 0, perché qualsiasi numero diviso per infinito è uguale a zero.

Esercizi risolti sui limiti all’infinito

Esercizio 1

Trovare i seguenti limiti della funzione grafica:

$\displaystyle\lim_{x\to -\infty}f(x)$

$\displaystyle\lim_{x\to +\infty}f(x)$

$\displaystyle\lim_{x\to -1^-}f(x)$

$\displaystyle\lim_{x\to -1^+}f(x)$

$\displaystyle\lim_{x\to 1^-}f(x)$

$\displaystyle\lim_{x\to 1^+}f(x)$

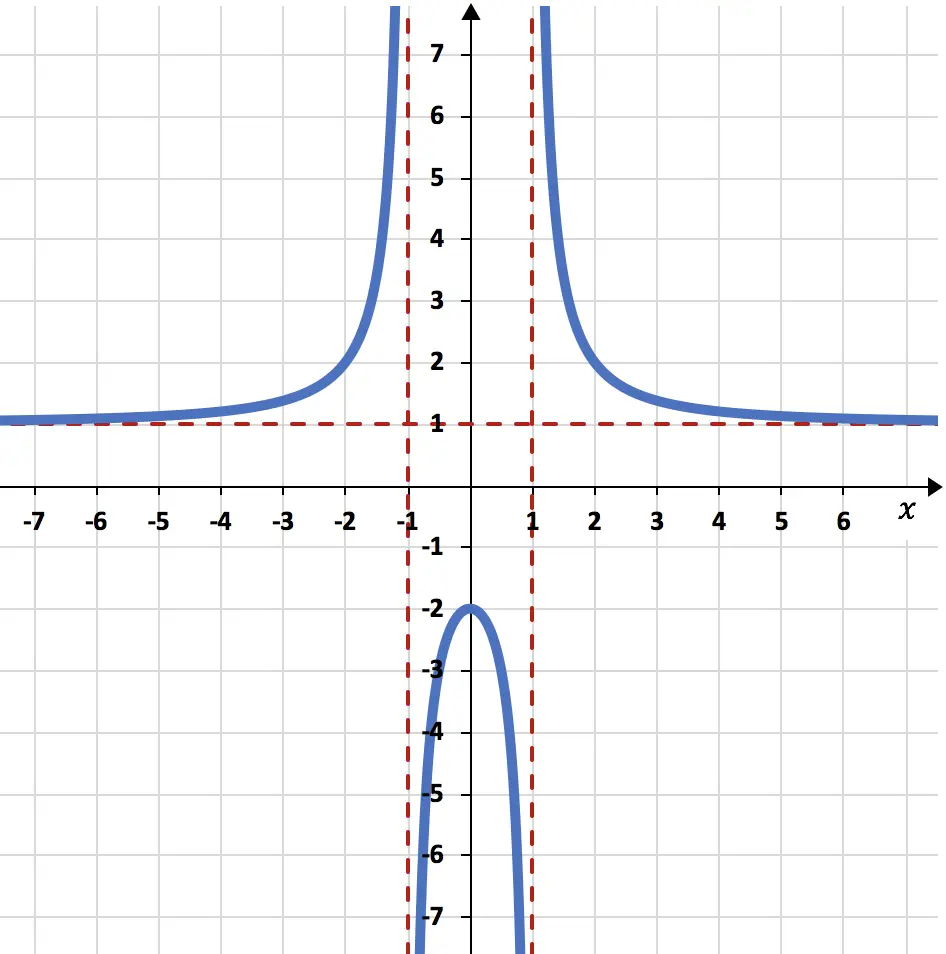
limiti all'infinito dalla rappresentazione di una funzione

Vedi la soluzione

Il limite della funzione quando x tende a meno infinito e più infinito dà 1:

$\displaystyle\lim_{x\to -\infty}f(x)=1$

$\displaystyle\lim_{x\to +\infty}f(x)=1$

I limiti laterali della funzione a sinistra e a destra nel punto x=-1 sono rispettivamente più infinito e meno infinito:

$\displaystyle\lim_{x\to -1^-}f(x)=+\infty$

$\displaystyle\lim_{x\to -1^+}f(x)=-\infty$

Infine, i limiti laterali della funzione quando x tende a 1 valgono meno infinito e più infinito:

$\displaystyle\lim_{x\to 1^-}f(x)=-\infty$

$\displaystyle\lim_{x\to 1^+}f(x)=+\infty$

Esercizio 2

Risolvi il limite quando x si avvicina all’infinito della seguente funzione:

$\displaystyle \lim_{x \to +\infty} (x^2+4x+1)$

Vedi la soluzione

Per risolvere il limite all’infinito, dobbiamo sostituire x con infinito nel termine di grado più alto del polinomio:

$\displaystyle \lim_{x \to +\infty} (x^2+4x+1) = (+\infty)^2= \bm{+\infty}$

Esercizio 3

Calcolare il limite all’infinito della seguente funzione polinomiale:

$\displaystyle \lim_{x \to +\infty} (-3x^2+8x+5)$

Vedi la soluzione

Per risolvere il limite all’infinito, sostituiamo x con infinito nel termine di grado più alto del polinomio ed eseguiamo i calcoli:

$\displaystyle \lim_{x \to +\infty} (-3x^2+8x+5) = -3(+\infty)^2= -3\cdot (+\infty) = \bm{-\infty}$

Esercizio 4

Risolvi il limite almeno infinito della seguente funzione polinomiale:

$\displaystyle \lim_{x \to -\infty} (6x^2-3x-4)$

Vedi la soluzione

Per calcolare il limite all’infinito, sostituiamo x con meno infinito nel termine di grado più alto del polinomio e valutiamo la funzione:

$\displaystyle \lim_{x \to -\infty} (6x^2-3x-4) = 6(-\infty)^2= 6\cdot (+\infty) = \bm{+\infty}$

Poiché meno infinito è al quadrato, il segno dell’infinito diventa positivo.

Esercizio 5

Trovare il limite all’infinito della seguente funzione razionale:

$\displaystyle \lim_{x \to +\infty}\frac{7}{2x-5}$

Vedi la soluzione

Per determinare il limite all’infinito, sostituiamo x con più infinito al termine del grado più alto del numeratore e del denominatore della frazione:

$\displaystyle \lim_{x \to +\infty}\frac{7}{2x-5} = \cfrac{7}{2\cdot(+\infty)}=\frac{7}{+\infty}=\bm{0}$

Ricorda che qualsiasi numero diviso per più o meno infinito è uguale a 0.

Esercizio 6

Risolvi il seguente limite all’infinito:

$\displaystyle \lim_{x \to -\infty} (-x^3+x^2+5x)$

Vedi la soluzione

Per calcolare il limite quando x tende a ±∞ di una funzione, basta guardare il monomio del grado più alto della funzione:

$\displaystyle \lim_{x \to -\infty} (-x^3+x^2+5x) = -(-\infty)^3= -(-\infty)= \bm{+\infty}$

Esercizio 7

Calcola il limite della seguente funzione quando x si avvicina all’infinito negativo:

$\displaystyle \lim_{x \to -\infty} (-4x^2+4)$

Vedi la soluzione

In questo caso è sufficiente sostituire il termine quadratico con infinito:

$\displaystyle \lim_{x \to -\infty} (-4x^2+4) = -4(-\infty)^2= -4\cdot (+\infty) = \bm{-\infty}$

Esercizio 8

Trova il limite della seguente funzione esponenziale quando x tende all’infinito:

$\displaystyle \lim_{x \to +\infty} 2^x$

Vedi la soluzione

Sebbene sia una funzione esponenziale, il procedimento per risolvere il limite è lo stesso: sostituire x con infinito.

$\displaystyle \lim_{x \to +\infty} 2^x = 2^{+\infty}=\bm{+\infty}$

Esercizio 9

Risolvi il limite infinito della seguente funzione esponenziale:

$\displaystyle \lim_{x \to +\infty} 5^{-x}$

Vedi la soluzione

Per risolvere questo limite è necessario utilizzare le proprietà delle frazioni:

$\displaystyle \lim_{x \to +\infty} 5^{-x} = 5^{-(+\infty)}=5^{-\infty}= \cfrac{1}{5^{+\infty}}= \cfrac{1}{\infty} =\bm{0}$

Esercizio 10

Risolvi il seguente limite all’infinito:

$\displaystyle \lim_{x \to +\infty} \cfrac{-4x^2+3}{3x+1}$

Vedi la soluzione

Il limite dà l’indeterminazione meno infinito tra più infinito. Il grado del numeratore è maggiore del grado del denominatore, quindi il limite indeterminato è uguale a più infinito. Tuttavia, poiché la divisione è infinito negativo per infinito positivo, il risultato è infinito negativo.

$\displaystyle \lim_{x \to +\infty} \cfrac{-4x^2+3}{3x+1} = \cfrac{-4(+\infty)^2}{3(+\infty)} =\cfrac{-4(+\infty)}{+\infty}= \cfrac{-\infty}{+\infty}= \bm{-\infty}$

Esercizio 11

Correggi il seguente limite indeterminato:

$\displaystyle \lim_{x \to +\infty} \cfrac{5x+8}{-5x+2}$

Vedi la soluzione

In questo problema, la forma indeterminata infinito su infinito si ottiene dal quoziente di due polinomi dello stesso grado, quindi il risultato del limite indeterminato è la divisione dei loro coefficienti principali:

$\displaystyle \lim_{x \to +\infty} \cfrac{5x+8}{-5x+2} = \cfrac{5(+\infty)}{-5(+\infty)} = \cfrac{+\infty}{-\infty}=\cfrac{5}{-5}= \bm{-1}$

Esercizio 12

Calcolare almeno all’infinito il seguente limite:

$\displaystyle \lim_{x \to -\infty} \cfrac{x^2+3x+5}{x^4-x-6}$

Vedi la soluzione

Il grado di espressione algebrica del numeratore è inferiore al grado di espressione del denominatore, quindi l’indeterminazione +∞/+∞ dà 0:

$\displaystyle \lim_{x \to -\infty} \cfrac{x^2+3x+5}{x^4-x-6} = \cfrac{(-\infty)^2}{(-\infty)^4} = \cfrac{+\infty}{+\infty}= \bm{0}$

Esercizio 13

Risolvi il seguente limite indeterminato di una funzione con radici:

$\displaystyle\lim_{x\to +\infty}\frac{\sqrt[3]{x^7-4x^3}}{x^2+5x}$

Vedi la soluzione

L’espressione del numeratore è sotto radicale, il suo grado è quindi 7/3. D’altra parte, il polinomio del denominatore è quadratico. E poiché 7/3>2, il limite dà più infinito:

$\displaystyle \lim_{x \to +\infty}\frac{\sqrt[3]{x^7-4x^3}}{x^2+5x}=\frac{\sqrt[3]{(+\infty)^7}}{(+\infty)^2}=\frac{+\infty}{+\infty}=\bm{+\infty}$

Esercizio 14

Determina il limite infinito della seguente funzione con le frazioni:

$\displaystyle\lim_{x \to +\infty} \cfrac{-2x^2}{5-4x}$

Vedi la soluzione

In questo esercizio otteniamo l’indeterminazione meno infinito diviso meno infinito con il grado del numeratore maggiore del grado del denominatore, quindi:

$\displaystyle \lim_{x \to +\infty} \cfrac{-2x^2}{5-4x} = \cfrac{-2(+\infty)^2}{-4(+\infty)} = \cfrac{-2(+\infty)}{-\infty}= \cfrac{-\infty}{-\infty} =\bm{+\infty}$

Esercizio 15

Trovare il limite almeno infinito della seguente funzione:

$\displaystyle \lim_{x \to -\infty} \cfrac{9x}{4-x^2}$

Vedi la soluzione

Il polinomio al denominatore è quadratico, mentre il polinomio al numeratore è lineare. Pertanto, l’indeterminatezza infinita divisa per infinito dà 0.

$\displaystyle \lim_{x \to -\infty} \cfrac{9x}{4-x^2} = \cfrac{9(-\infty)}{-(-\infty)^2} = \cfrac{-\infty}{-(+\infty)}=\cfrac{-\infty}{-\infty}= \bm{0}$

Esercizio 16

Risolvi il limite almeno infinito della seguente funzione:

$\displaystyle \lim_{x \to -\infty} \cfrac{-2x^3-3x}{-3x^2+4x-1}$

Vedi la soluzione

Il numeratore è un grado maggiore del denominatore, quindi il risultato della forma indeterminata ∞/∞ sarà infinito. Inoltre, il segno dell’infinito sarà negativo perché il positivo tra il negativo si traduce in negativo:

$\displaystyle \lim_{x \to -\infty} \cfrac{-2x^3-3x}{-3x^2+4x-1} = \cfrac{-2(-\infty)^3}{-3(-\infty)^2} =\cfrac{-2(-\infty)}{-3(+\infty)}= \cfrac{+\infty}{-\infty}= \bm{-\infty}$

Esercizio 17

Risolvi il seguente limite all’infinito:

$\displaystyle\lim_{x \to +\infty}\cfrac{2^x-4}{-2x^6+x^4}$

Vedi la soluzione

La funzione esponenziale è di ordine superiore rispetto alla funzione polinomiale, quindi il limite darà infinito. Tuttavia, dividendo il positivo per il negativo, il segno dell’infinito sarà negativo:

$\displaystyle\lim_{x \to +\infty}\frac{2^x-4}{-2x^6+x^4}=\frac{2^{+\infty}}{-2(+\infty)^6}=\frac{+\infty}{-\infty}=\bm{-\infty}$

Esercizio 18

Calcola il limite infinito della seguente funzione con radice quadrata:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt{4x^2+1}}{-2x}$

Vedi la soluzione

Il numeratore è formato da una radice quadrata, il suo grado è quindi 2/2=1. Allora, il grado del numeratore è uguale a quello del denominatore, quindi l’infinita indeterminazione tra infinito si risolve come segue:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt{4x^2+1}}{-2x}= \cfrac{\sqrt{4(+\infty)^2}}{-2(\infty)}= \cfrac{+\infty}{-\infty} = \cfrac{\sqrt{4}}{-2}=\cfrac{2}{-2}=\bm{-1}$

Esercizio 19

Risolvi il limite infinito della seguente funzione con due radicali:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[3]{6x^7+2x^3}}{\sqrt{x^5-3x^4+2x}}$

Vedi la soluzione

Il grado del numeratore è 7/3=2,33 e il grado del denominatore è 5/2=2,5. Pertanto, poiché il grado del numeratore è inferiore al grado del denominatore, il limite infinito indeterminato tra l’infinito è 0:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[3]{6x^7+2x^3}}{\sqrt{x^5-3x^4+2x}}=\cfrac{\sqrt[3]{6(+\infty)^7}}{\sqrt{(+\infty)^5}}=\cfrac{+\infty}{+\infty}=\bm{0}$

Esercizio 20

Calcolare il seguente limite:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[5]{x^7-2x^5-1}}{4^{x-2}+3x}$

Vedi la soluzione

Indipendentemente dal grado del numeratore, poiché abbiamo una funzione esponenziale al denominatore, il risultato della forma indeterminata infinito su infinito è 0:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[5]{x^7-2x^5-1}}{4^{x-2}+3x}=\cfrac{\sqrt[5]{(+\infty)^7}}{4^{+\infty-2}}=\cfrac{+\infty}{+\infty}=\bm{0}$

Esercizio 21

Determinare il limite infinito della seguente funzione razionale:

$\displaystyle\lim_{x\to +\infty}\left(\frac{x^3+1}{x-1}-\frac{x}{4} \right)$

Vedi la soluzione

Per prima cosa proviamo a calcolare il limite sostituendo l’infinito nella funzione:

$\displaystyle\lim_{x\to +\infty}\left(\frac{x^3+1}{x-1}-\frac{x}{4}\right)=\frac{(+\infty)^3+1}{+\infty-1}-\frac{+\infty}{4} = \bm{+\infty -\infty}$

Ma troviamo l’indeterminazione ∞ – ∞. Pertanto, riduciamo le frazioni a un denominatore comune:

$\begin{array}{l}\displaystyle\lim\limits_{x \to +\infty} \left(\frac{x^3+1}{x-1}-\frac{x}{4} \right)=\\[5ex]\displaystyle = \lim_{x\to +\infty}\left(\frac{(x^3+1)\cdot4}{(x-1)\cdot4}-\frac{x\cdot(x-1)}{4\cdot (x-1)}\right)=\\[5ex]\displaystyle =\lim_{x\to +\infty}\left(\frac{4x^3+4}{4x-4}-\frac{x^2-x}{4x-4}\right)\end{array}$

E poiché le due frazioni ora hanno lo stesso denominatore, possiamo combinarle in un’unica frazione:

$\displaystyle\lim_{x \to +\infty}\left(\frac{4x^3+4}{4x-4}-\frac{x^2-x}{4x-4}\right)=\lim_{x\to +\infty}\frac{4x^3+4-(x^2-x)}{4x-4}$

Scriviamo le parentesi del numeratore:

$\displaystyle\lim_{x \to +\infty} \frac{4x^3+4-x^2+x}{4x-4}$

E infine, determiniamo il limite:

$\displaystyle\lim_{x \to +\infty}\frac{4x^3+4-x^2+x}{4x-4}=\frac{4(+\infty)^3}{4(+\infty)}=\frac{+\infty}{+\infty} = \bm{+\infty}$

In questo caso l’indeterminazione ∞/∞ dà +∞ perché il grado del numeratore è maggiore del grado del denominatore.

Esercizio 22

Risolvi il limite della seguente funzione frazionaria quando x si avvicina a 0:

$\displaystyle\lim_{x\to 0}\left(\frac{-3x-2}{x^4}-\frac{5}{x^2}\right)$

Vedi la soluzione

Proviamo innanzitutto a calcolare il limite come al solito:

$\displaystyle\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5}{x^2}\right)=\frac{-3\cdot0-2}{0^4}-\frac{5}{0^2}=\frac{-2}{0}-\frac{5}{0}=\bm{\infty-\infty}$

Ma otteniamo la forma indeterminata ∞-∞. Dobbiamo quindi ridurre le frazioni della funzione ad un denominatore comune.

In questo caso x ⁴ è un multiplo di x ² , quindi semplicemente moltiplicando il numeratore e il denominatore della seconda frazione per x ² ci assicureremo che entrambe le frazioni abbiano lo stesso denominatore:

$\begin{array}{l}\displaystyle\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5}{x^2}\right)=\\[5ex]\displaystyle =\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5\cdot x^2}{x^2\cdot x^2} \right)=\\[5ex]\displaystyle =\lim_{x\to 0}\left(\frac{-3x-2}{x^4}-\frac{5x^2}{x^4}\right)\end{array}$

Ora possiamo sottrarre le due frazioni:

$\displaystyle\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5x^2}{x^4}\right)=\lim_{x\to 0}\frac{-3x-2-5x^2 }{x^4}$

Proviamo a risolvere nuovamente il limite:

$\displaystyle \lim_{x \to 0} \cfrac{-3x-2-5x^2 }{x^4} =\cfrac{-3\cdot 0-2-5\cdot 0^2}{0^4}=\frac{-2}{0}$

Ma ci ritroviamo con l’indeterminatezza di una costante che parte da zero. È quindi necessario calcolare i limiti laterali della funzione.

$\displaystyle\lim_{x \to 0^{-}} \frac{-3x-2-5x^2}{x^4}=\frac{-2}{+0}=-\infty$

$\displaystyle\lim_{x \to 0^{+}}\frac{-3x-2-5x^2}{x^4}=\frac{-2}{+0}=-\infty$

In conclusione, poiché i due limiti laterali della funzione nel punto x=0 danno -∞, la soluzione del limite è -∞:

$\displaystyle \lim_{x \to 0^-}f(x)=\lim_{x \to 0^+}f(x)=-\infty\ \longrightarrow \ \lim_{x \to 0}f(x)= \bm{-\infty}$

Esercizio 23

Risolvi il limite infinito della seguente funzione con radici:

$\displaystyle\lim_{x\to +\infty}\left(4x^2-\sqrt{x^4+1}\right)$

Vedi la soluzione

Cercando di risolvere il limite, otteniamo l’indeterminazione infinito meno infinito:

$\displaystyle\lim_{x\to +\infty}\left(4x^2-\sqrt{x^4+1}\right)=4(+\infty)^2-\sqrt{(+\infty)^4}=\bm{+\infty -\infty}$

Pertanto, poiché nella funzione sono presenti radicali, è necessario moltiplicarla e dividerla per l’espressione radicale coniugata:

$\displaystyle\lim_{x \to +\infty}\left(4x^2-\sqrt{x^4+1} \right)=\lim_{x \to +\infty}\frac{\left(4x^2-\sqrt{x^4+1}\right)\cdot\left(4x^2+\sqrt{x^4+1}\right)}{4x^2+\sqrt{x^4+1}}$

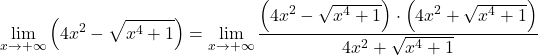
Al numeratore abbiamo il prodotto notevole di una somma per una differenza, che è uguale alla differenza dei quadrati. Ancora:

$\displaystyle\lim_{x\to +\infty}\frac{\left(4x^2\right)^2-\left(\sqrt{x^4+1}\right)^2}{4x^2+\sqrt{x^4+1}}$

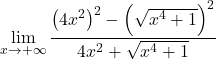
Semplifichiamo il radicale al quadrato:

$\displaystyle\lim_{x\to +\infty}\frac{\bigl(4x^2\bigr)^2-(x^4+1)}{4x^2+\sqrt{x^4+1}}$

Operiamo sul numeratore:

$\displaystyle\lim_{x\to +\infty}\frac{16x^4-x^4-1}{4x^2+\sqrt{x^4+1}}$

$\displaystyle\lim_{x\to +\infty}\frac{15x^4-1}{4x^2+\sqrt{x^4+1}}$

E infine troviamo il limite:

$\displaystyle\lim_{x\to +\infty}\frac{15x^4-1}{4x^2+\sqrt{x^4+1}}=\frac{15(+\infty)^4}{4(+\infty)^2+\sqrt{(+\infty)^4}}=\frac{+\infty}{+\infty}= \bm{+\infty}$

In questo caso l’indeterminazione infinito diviso infinito è più infinita perché il grado del numeratore è maggiore del grado del denominatore (ricordiamo che la radice quadrata riduce il grado di due:

$\sqrt{x^4} = x^{4/2} = x^2$

Esercizio 24

Risolvi il limite per x che tende all’infinito della seguente funzione irrazionale:

$\displaystyle\lim_{x\to +\infty}\left(2x-1-\sqrt{4x^2+1}\right)$

Vedi la soluzione

Per prima cosa proviamo a calcolare il limite come al solito:

$\displaystyle\lim_{x\to +\infty}\left(2x-1-\sqrt{4x^2+1}\right)=2(+\infty)-\sqrt{4(+\infty)^2}=\bm{+\infty -\infty}$

Ma ciò porta all’indeterminazione della differenza degli infiniti. Pertanto, poiché la funzione ha radici, dobbiamo moltiplicare e dividere l’espressione per il radicale coniugato:

$\displaystyle\lim_{x\to +\infty}\frac{\left(2x-1-\sqrt{4x^2+1}\right)\cdot\left(2x-1+\sqrt{4x^2+1}\right)}{2x-1 +\sqrt{4x^2+1}}$

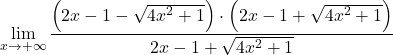
Raggruppiamo l’uguaglianza notevole del numeratore della frazione:

$\displaystyle\lim_{x\to +\infty}\frac{\left(2x-1\right)^2-\left(\sqrt{4x^2+1}\right)^2}{2x-1+\sqrt{4x^2+1}}$

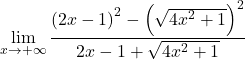
Risolviamo la radice quadrata:

$\displaystyle\lim_{x\to +\infty}\frac{\left(2x-1\right)^2-\left(4x^2+1\right)}{2x-1+\sqrt{4x^2+1}}$

Risolviamo l’identità notevole del quadrato di una differenza:

$\displaystyle\lim_{x\to +\infty}\frac{4x^2+1-4x-\left(4x^2+1\right)}{2x-1+\sqrt{4x^2+1}}$

Operiamo sul numeratore:

$\displaystyle\lim_{x\to +\infty}\frac{4x^2+1-4x-4x^2-1}{2x-1+\sqrt{4x^2+1}}$

$\displaystyle\lim_{x \to +\infty}\frac{-4x}{2x-1+\sqrt{4x^2+1}}$

E infine calcoliamo il valore del limite all’infinito:

$\displaystyle\lim_{x \to +\infty} \cfrac{-4x }{2x-1 +\sqrt{4x^2+1} } = \cfrac{-4(+\infty) }{2(+\infty)+\sqrt{4(+\infty)^2} } = \cfrac{-\infty}{+\infty} =$

Anche se c’è una x al quadrato al denominatore, il suo grado in realtà è 1 perché è all’interno di una radice:

$\sqrt{4x^2} =\sqrt{4}\cdot \sqrt{x^2} = \sqrt{4}\cdot x^{2/2} =\sqrt{4} x^1=\sqrt{4}x .$

Pertanto il risultato dell’indeterminazione -∞/+∞ è la divisione dei coefficienti delle x di massimo grado, poiché il grado del numeratore è uguale al grado del denominatore.

$\displaystyle\lim_{x\to +\infty}\frac{-4x}{2x-1+\sqrt{4x^2+1} }=\frac{-\infty}{+\infty}=\frac{-4}{2+\sqrt{4}}=\frac{-4}{2+2}=\frac{-4}{4}=\bm{-1}$

Nota che poiché ci sono due termini di primo grado al denominatore

$\bigl(2x$

$\sqrt{4x^2}\bigr)$

, per risolvere l’indeterminazione -∞/+∞ occorre prendere tutti i coefficienti dei termini di primo grado, cioè i

$2$

$2x$

e il

$\sqrt{4}$

$\sqrt{4x^2}.$

Esercizio 25

Calcola il limite quando x tende a 1 della seguente funzione con frazioni:

$\displaystyle\lim_{x\to 1}\left(\frac{1}{1-x}-\frac{3}{1-x^3}\right)$

Vedi la soluzione

Provando a fare il limite otteniamo il limite indeterminato di infinito meno infinito:

$\displaystyle\lim_{x\to 1}\left(\frac{1}{1-x}-\frac{3}{1-x^3}\right)=\frac{1}{1-1}--\frac{3}{1-1^3}=\frac{1}{0}-\frac{3}{0}=\bm{\infty-\infty}$

Dobbiamo quindi ridurre le frazioni ad un denominatore comune, o in altre parole dobbiamo moltiplicare il numeratore e il denominatore di una frazione per il denominatore dell’altra:

$\begin{array}{l}\displaystyle\lim_{x \to 1}\left(\frac{1}{1-x}-\frac{3}{1-x^3} \right)=\\[5ex]\displaystyle =\lim_{x\to 1}\left( \frac{1\cdot(1-x^3)}{(1-x)\cdot(1-x^3)}-\frac{3\cdot(1-x)}{(1-x^3)\cdot(1-x)}\right)=\\[5ex]\displaystyle =\lim_{x \to 1}\left(\frac{1-x^3}{1-x-x^3+x^4}-\frac{3-3x}{1-x-x^3+x^4}\right)\end{array}$

E poiché ora le due frazioni hanno lo stesso denominatore, possiamo metterle insieme:

$\displaystyle\lim_{x \to 1}\left(\frac{1-x^3}{1-x-x^3+x^4}-\frac{3-3x}{1-x-x^3+x^4}\right)=\lim_{x\to 1}\frac{1-x^3-(3-3x)}{1-x-x^3+x^4}$

Operiamo:

$\displaystyle\lim_{x \to 1} \cfrac{1-x^3-3+3x}{1-x-x^3+x^4}$

$\displaystyle\lim_{x \to 1} \cfrac{-x^3+3x-2}{x^4-x^3-x+1}$

E proviamo di nuovo a risolvere il limite:

$\displaystyle\lim_{x \to 1}\frac{-x^3+3x-2}{x^4-x^3-x+1}=\frac{-1^3+3\cdot1-2}{1^4-1^3-1+1}=\mathbf{\frac{0}{0}}$

Ma troviamo l’indeterminazione zero divisa per zero. Dobbiamo quindi fattorizzare i polinomi del numeratore e del denominatore:

$\displaystyle\lim_{x \to 1}\frac{-x^3+3x-2}{x^4-x^3-x+1}=\lim_{x \to 1}\frac{-(x-1)^2(x+2)}{(x-1)^2(x^2+x+1)}$

Ora semplifichiamo la frazione eliminando il fattore che si ripete al numeratore e al denominatore:

$\displaystyle\lim_{x \to 1}\frac{-\cancel{(x-1)^2}(x+2)}{\cancel{(x-1)^2}(x^2+x+1)}=\lim_{x \to 1}\frac{-(x+2)}{x^2+x+1}$

E infine, risolviamo il limite:

$\displaystyle\lim_{x \to 1}\frac{-(x+2)}{x^2+x+1}=\frac{-(1+2)}{1^2+1+1}=\frac{-3}{3}=\bm{-1}$

Limiti all'infinito

Limite di una funzione quando x tende all’infinito

Come risolvere i limiti all’infinito

Esempi di limiti all’infinito

Limiti indeterminati all’infinito

Infinita indeterminatezza tra gli infiniti

Infinita indeterminatezza tra l’infinito con radici

Indeterminazione infinita tra infinito con funzioni esponenziali

Infinito meno infinita indeterminatezza

Indeterminazione infinito meno infinito con le frazioni

Indeterminazione infinito meno infinito con radici

Esercizi risolti sui limiti all’infinito

Esercizio 1

Esercizio 2

Esercizio 3

Esercizio 4

Esercizio 5

Esercizio 6

Esercizio 7

Esercizio 8

Esercizio 9

Esercizio 10

Esercizio 11

Esercizio 12

Esercizio 13

Esercizio 14

Esercizio 15

Esercizio 16

Esercizio 17

Esercizio 18

Esercizio 19

Esercizio 20

Esercizio 21

Esercizio 22

Esercizio 23

Esercizio 24

Esercizio 25

Lascia un commento Annulla risposta