Indeterminazione infinito meno infinito (∞-∞)

In questo articolo spieghiamo come risolvere l’indeterminazione infinito meno infinito (∞-∞). Troverai esempi di questa indeterminazione con diversi tipi di funzioni e, inoltre, potrai esercitarti con esercizi risolti passo dopo passo sull’indeterminazione infinito meno infinito.

Risolvere l’indeterminazione infinito meno infinito

Quando il limite di una funzione dà infinito meno infinito, significa che si tratta di un’indeterminazione (o di una forma indeterminata). Cioè il limite di una funzione che dà indeterminazione meno infinito non può essere determinato eseguendo il calcolo diretto, ma occorre piuttosto effettuare una procedura preliminare.

Quindi, per risolvere l’indeterminatezza infinito meno infinito, dobbiamo prima applicare un procedimento che dipende dal tipo di funzione: se è una funzione polinomiale, si può calcolare per confronto, se è una funzione razionale, le frazioni devono essere ridotte a un denominatore comune e, se è una funzione irrazionale, deve essere moltiplicata per il coniugato.

$\displaystyle\lim_{x\to+\infty}\Bigl(f(x)-g(x)\Bigr)=\infty-\infty$

Successivamente vedremo con esempi come viene risolta l’indeterminazione infinito meno infinito in ciascun tipo di funzione.

Infinito meno infinita indeterminazione nelle funzioni polinomiali

In un polinomio, l’indeterminazione infinito meno infinito è uguale all’infinito di ordine massimo, ovvero il termine di ordine massimo determina il segno positivo o negativo dell’infinito.

Ad esempio, considera il limite della seguente funzione polinomiale che dà la forma indeterminata infinito meno infinito:

$\displaystyle\lim_{x\to+\infty}\bigl(x^2-3x\bigr)=(+\infty)^2-3\cdot (\infty)=+\infty-\infty=+\infty$

In questo caso il termine x ² è di secondo grado e il termine 3x è di primo grado, quindi il monomio x ² è dominante perché di ordine superiore. Pertanto il risultato del limite è l’infinito ottenuto da questo termine.

Dai un’occhiata a questi altri esempi:

$\begin{array}{l}\displaystyle\lim_{x\to+\infty}\bigl(x^5-4x^2-3x\bigr)=(+\infty)^5=+\infty\\[5ex]\displaystyle\lim_{x\to-\infty}\bigl(-3x^2-5x\bigr)=-3\cdot (-\infty)^2=-3\cdot \infty=-\infty\\[5ex]\displaystyle\lim_{x\to+\infty}\bigl(x^7-5x^4+x^3-2x-10\bigr)=(+\infty)^7=+\infty\end{array}$

In breve, quando poniamo limiti all’infinito nelle funzioni polinomiali , dobbiamo semplicemente sostituire l’infinito nel termine di grado più alto , ignorando tutti gli altri termini.

Indeterminazione infinito meno infinito con le frazioni

Quando l’indeterminazione infinito meno infinito si verifica in un’addizione o sottrazione di frazioni algebriche , dobbiamo prima fare l’addizione o la sottrazione delle frazioni e poi calcolare il limite.

Vediamo come calcolare l’indeterminazione infinito meno infinito in una funzione con frazioni risolvendo passo passo un esempio:

$\displaystyle \lim_{x \to +\infty} \left( \frac{x^2}{x-1} - \frac{x}{3}\right)$

Proviamo prima a calcolare il limite:

$\displaystyle \lim_{x \to +\infty}\left( \frac{x^2}{x-1} - \frac{x}{3}\right) = \frac{(+\infty)^2}{(+\infty)-1} - \frac{+\infty}{3} = \bm{+\infty - \infty}$

Ma otteniamo l’indeterminazione ∞-∞.

Quindi prima dobbiamo fare la sottrazione delle frazioni. Per fare ciò, riduciamo le frazioni a un denominatore comune, ovvero moltiplichiamo il numeratore e il denominatore di una frazione per il denominatore dell’altra:

$\begin{array}{l}\displaystyle\lim_{x \to +\infty} \left( \frac{x^2}{x-1}-\frac{x}{3}\right)=\\[5ex]\displaystyle =\lim_{x \to +\infty}\left(\frac{x^2 \cdot 3}{(x-1)\cdot 3}- \frac{x\cdot (x-1)}{3\cdot (x-1)} \right)=\\[5ex]\displaystyle = \lim_{x \to +\infty} \left( \frac{3x^2 }{3(x-1)}- \frac{x^2-x}{3(x-1)}\right)\end{array}$

E ora che entrambe le frazioni hanno lo stesso denominatore, possiamo combinarle in un’unica frazione:

$\displaystyle \lim_{x \to +\infty} \frac{3x^2 -(x^2-x)}{3(x-1)}$

Operiamo al numeratore e al denominatore:

$\displaystyle \lim_{x \to +\infty} \frac{3x^2 -x^2+x}{3x-3} = \lim_{x \to +\infty} \frac{2x^2+x}{3x-3}$

E infine, calcoliamo nuovamente il limite:

$\displaystyle \lim_{x \to +\infty}\frac{2x^2+x}{3x-3}=\frac{+\infty}{+\infty}=\bm{+\infty}$

In questo caso l’infinita indeterminazione tra infinito dà +∞ perché il grado del numeratore è maggiore del grado del denominatore.

➤ Vedi: cos’è l’infinito tra l’infinito?

indeterminazione infinito meno infinito con radici

Quando l’indeterminazione infinito meno infinito si verifica nell’addizione o nella sottrazione radicale , dobbiamo prima moltiplicare e dividere la funzione per l’espressione radicale coniugata, quindi risolvere il limite.

Vedremo come risolvere l’indeterminazione infinito meno infinito in una funzione irrazionale utilizzando un esempio passo passo:

$\displaystyle\lim_{x\to +\infty}\left(x-\sqrt{x^2-5}\right)$

Proviamo prima a risolvere il limite della funzione con i radicali:

$\displaystyle\lim_{x\to +\infty}\left(x-\sqrt{x^2-5}\right)=+\infty-\sqrt{(+\infty)^2}=\bm{+\infty-\infty}$

Tuttavia, otteniamo la forma indeterminata ∞-∞. Quindi, per sapere quanta indeterminazione è infinito meno infinito, dobbiamo applicare la procedura spiegata.

Poiché la funzione ha radicali, moltiplichiamo e dividiamo l’intera funzione per l’espressione irrazionale coniugata:

$\displaystyle\lim_{x \to +\infty}\left(x-\sqrt{x^2-5}\right)= \lim_{x \to +\infty}\frac{\left(x-\sqrt{x^2-5}\right)\cdot\left(x+\sqrt{x^2-5}\right)}{x+\sqrt{x^2-5}}$

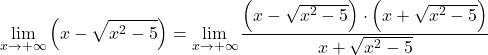
L’espressione algebrica del numeratore corrisponde all’identità notevole del prodotto di una somma per una differenza, possiamo quindi semplificare l’espressione:

$\displaystyle \lim_{x \to +\infty} \cfrac{\left(x-\sqrt{x^2-5}\right) \cdot \left(x + \sqrt{x^2-5}\right)}{ x + \sqrt{x^2-5}}= \lim_{x \to +\infty} \cfrac{x^2- \left( \sqrt{x^2-5}\right)^2}{ x + \sqrt{x^2-5}}$

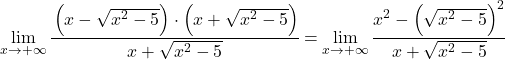
Semplifichiamo ora la radice del limite, poiché è quadrata:

$\displaystyle \lim_{x \to +\infty}\frac{x^2-(x^2-5)}{x+\sqrt{x^2-5}}$

Operiamo sul numeratore della frazione:

$\displaystyle \lim_{x \to +\infty} \frac{x^2- x^2+5}{x+\sqrt{x^2-5}}$

$\displaystyle \lim_{x \to +\infty} \frac{5}{x+\sqrt{x^2-5}}$

E infine, rifacciamo il calcolo del limite:

$\displaystyle \lim_{x \to +\infty} \frac{5}{x+\sqrt{x^2-5}}=\frac{5}{+\infty+\sqrt{(+\infty)^2}}=\frac{5}{+\infty}=\bm{0}$

Il risultato del limite è quindi 0, perché qualsiasi numero diviso per infinito è uguale a zero.

Risolti problemi di indeterminazione infinita meno infinita

Esercizio 1

Risolvi il seguente limite quando x si avvicina a più infinito:

$\displaystyle\lim_{x\to +\infty}(7x^2-2x^3)$

vedi soluzione

In questo limite il termine di ordine più alto è di terzo grado, quindi ci concentriamo sull’infinito ottenuto da questo termine.

$\displaystyle\lim_{x\to +\infty}(+7x^2-2x^3)=+\infty^2-\infty^3=+\infty-\infty=\bm{-\infty}$

Esercizio 2

Calcola il limite della seguente funzione polinomiale quando x si avvicina all’infinito negativo:

$\displaystyle\lim_{x\to -\infty}(-5x^3-9x^2)$

vedi soluzione

L’infinito negativo al cubo rimane negativo, ma al quadrato diventa positivo. in seguito Sebbene i loro segni siano modificati dai coefficienti che li precedono:

$\begin{array}{l}\displaystyle\lim_{x\to -\infty}(-5x^3+x^2)=\\[3ex]=-5(-\infty)^3-9(-\infty)^2=\\[3ex]=-5\cdot (-\infty)-9\cdot \infty=\\[3ex]=+\infty-\infty\end{array}$

Allora, la forma indeterminata infinito meno infinito è definita dal termine di ordine più alto (-5x ³ ), da cui si ottiene l’infinito positivo:

$\displaystyle\lim_{x\to -\infty}(-5x^3+x^2)=\bm{+\infty}$

Esercizio 3

Determinare il limite all’infinito della seguente funzione razionale:

$\displaystyle\lim_{x\to +\infty}\left(\frac{x^3+1}{x-1}-\frac{x}{4} \right)$

vedi soluzione

Per prima cosa proviamo a calcolare il limite sostituendo l’infinito nella funzione:

$\displaystyle\lim_{x\to +\infty}\left(\frac{x^3+1}{x-1}-\frac{x}{4}\right)=\frac{(+\infty)^3+1}{+\infty-1}-\frac{+\infty}{4} = \bm{+\infty -\infty}$

Ma ci ritroviamo con l’indeterminazione ∞ – ∞. Pertanto, riduciamo le frazioni a un denominatore comune:

$\begin{array}{l}\displaystyle\lim\limits_{x \to +\infty} \left(\frac{x^3+1}{x-1}-\frac{x}{4} \right)=\\[5ex]\displaystyle = \lim_{x\to +\infty}\left(\frac{(x^3+1)\cdot4}{(x-1)\cdot4}-\frac{x\cdot(x-1)}{4\cdot (x-1)}\right)=\\[5ex]\displaystyle =\lim_{x\to +\infty}\left(\frac{4x^3+4}{4x-4}-\frac{x^2-x}{4x-4}\right)\end{array}$

E poiché entrambe le frazioni ora hanno lo stesso denominatore, possiamo combinarle in un’unica frazione:

$\displaystyle\lim_{x \to +\infty}\left(\frac{4x^3+4}{4x-4}-\frac{x^2-x}{4x-4}\right)=\lim_{x\to +\infty}\frac{4x^3+4-(x^2-x)}{4x-4}$

Scriviamo le parentesi del numeratore:

$\displaystyle\lim_{x \to +\infty} \frac{4x^3+4-x^2+x}{4x-4}$

E, infine, determiniamo il limite:

$\displaystyle\lim_{x \to +\infty}\frac{4x^3+4-x^2+x}{4x-4}=\frac{4(+\infty)^3}{4(+\infty)}=\frac{+\infty}{+\infty} = \bm{+\infty}$

In questo caso l’indeterminazione ∞/∞ dà +∞ perché il grado del numeratore è maggiore del grado del denominatore.

Esercizio 4

Risolvi il limite della seguente funzione frazionaria quando x si avvicina a 0:

$\displaystyle\lim_{x\to 0}\left(\frac{-3x-2}{x^4}-\frac{5}{x^2}\right)$

vedi soluzione

Proviamo innanzitutto a calcolare il limite come al solito:

$\displaystyle\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5}{x^2}\right)=\frac{-3\cdot0-2}{0^4}-\frac{5}{0^2}=\frac{-2}{0}-\frac{5}{0}=\bm{\infty-\infty}$

Ma otteniamo la forma indeterminata ∞-∞. Pertanto, dobbiamo ridurre le frazioni della funzione a un denominatore comune.

In questo caso x ⁴ è multiplo di x ² , quindi semplicemente moltiplicando numeratore e denominatore della seconda frazione per x ² otterremo che entrambe le frazioni hanno lo stesso denominatore:

$\begin{array}{l}\displaystyle\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5}{x^2}\right)=\\[5ex]\displaystyle =\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5\cdot x^2}{x^2\cdot x^2} \right)=\\[5ex]\displaystyle =\lim_{x\to 0}\left(\frac{-3x-2}{x^4}-\frac{5x^2}{x^4}\right)\end{array}$

Ora possiamo sottrarre le due frazioni:

$\displaystyle\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5x^2}{x^4}\right)=\lim_{x\to 0}\frac{-3x-2-5x^2 }{x^4}$

Proviamo a risolvere nuovamente il limite:

$\displaystyle \lim_{x \to 0} \cfrac{-3x-2-5x^2 }{x^4} =\cfrac{-3\cdot 0-2-5\cdot 0^2}{0^4}=\frac{-2}{0}$

Ma ci ritroviamo con l’indeterminatezza di una costante divisa per zero. È quindi necessario calcolare i limiti laterali della funzione.

$\displaystyle\lim_{x \to 0^{-}} \frac{-3x-2-5x^2}{x^4}=\frac{-2}{+0}=-\infty$

$\displaystyle\lim_{x \to 0^{+}}\frac{-3x-2-5x^2}{x^4}=\frac{-2}{+0}=-\infty$

In conclusione, poiché i due limiti laterali della funzione nel punto x=0 danno -∞, la soluzione del limite è -∞:

$\displaystyle \lim_{x \to 0^-}f(x)=\lim_{x \to 0^+}f(x)=-\infty\ \longrightarrow \ \lim_{x \to 0}f(x)= \bm{-\infty}$

Esercizio 5

Risolvi il limite all’infinito della seguente funzione con radici:

$\displaystyle\lim_{x\to +\infty}\left(4x^2-\sqrt{x^4+1}\right)$

vedi soluzione

Cercando di risolvere il limite, otteniamo l’indeterminazione infinito meno infinito:

$\displaystyle\lim_{x\to +\infty}\left(4x^2-\sqrt{x^4+1}\right)=4(+\infty)^2-\sqrt{(+\infty)^4}=\bm{+\infty -\infty}$

Pertanto, poiché nella funzione sono presenti radicali, dobbiamo moltiplicarla e dividerla per l’espressione radicale coniugata:

$\displaystyle\lim_{x \to +\infty}\left(4x^2-\sqrt{x^4+1} \right)=\lim_{x \to +\infty}\frac{\left(4x^2-\sqrt{x^4+1}\right)\cdot\left(4x^2+\sqrt{x^4+1}\right)}{4x^2+\sqrt{x^4+1}}$

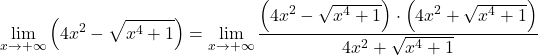
Al numeratore abbiamo il prodotto notevole di una somma per una differenza, che è uguale alla differenza dei quadrati. Ancora:

$\displaystyle\lim_{x\to +\infty}\frac{\left(4x^2\right)^2-\left(\sqrt{x^4+1}\right)^2}{4x^2+\sqrt{x^4+1}}$

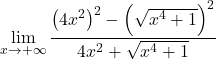
Semplifichiamo il radicale al quadrato:

$\displaystyle\lim_{x\to +\infty}\frac{\bigl(4x^2\bigr)^2-(x^4+1)}{4x^2+\sqrt{x^4+1}}$

Operiamo al numeratore:

$\displaystyle\lim_{x\to +\infty}\frac{16x^4-x^4-1}{4x^2+\sqrt{x^4+1}}$

$\displaystyle\lim_{x\to +\infty}\frac{15x^4-1}{4x^2+\sqrt{x^4+1}}$

E, infine, troviamo il limite:

$\displaystyle\lim_{x\to +\infty}\frac{15x^4-1}{4x^2+\sqrt{x^4+1}}=\frac{15(+\infty)^4}{4(+\infty)^2+\sqrt{(+\infty)^4}}=\frac{+\infty}{+\infty}= \bm{+\infty}$

In questo caso l’indeterminatezza infinita divisa per infinito è più infinita perché il grado del numeratore è maggiore del grado del denominatore (ricordiamo che la radice quadrata riduce il grado di due:

$\sqrt{x^4} = x^{4/2} = x^2$

Esercizio 6

Risolvi il limite per x che tende all’infinito della seguente funzione irrazionale:

$\displaystyle\lim_{x\to +\infty}\left(2x-1-\sqrt{4x^2+1}\right)$

vedi soluzione

Per prima cosa proviamo a calcolare il limite come al solito:

$\displaystyle\lim_{x\to +\infty}\left(2x-1-\sqrt{4x^2+1}\right)=2(+\infty)-\sqrt{4(+\infty)^2}=\bm{+\infty -\infty}$

Ma ci dà come risultato l’indeterminazione della differenza degli infiniti. Pertanto, poiché la funzione ha radici, dobbiamo moltiplicare e dividere l’espressione per il radicale coniugato:

$\displaystyle\lim_{x\to +\infty}\frac{\left(2x-1-\sqrt{4x^2+1}\right)\cdot\left(2x-1+\sqrt{4x^2+1}\right)}{2x-1 +\sqrt{4x^2+1}}$

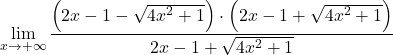
Raggruppiamo l’uguaglianza notevole del numeratore della frazione:

$\displaystyle\lim_{x\to +\infty}\frac{\left(2x-1\right)^2-\left(\sqrt{4x^2+1}\right)^2}{2x-1+\sqrt{4x^2+1}}$

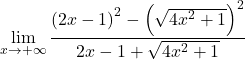
Risolviamo la radice quadrata:

$\displaystyle\lim_{x\to +\infty}\frac{\left(2x-1\right)^2-\left(4x^2+1\right)}{2x-1+\sqrt{4x^2+1}}$

Risolviamo l’identità notevole del quadrato di una differenza:

$\displaystyle\lim_{x\to +\infty}\frac{4x^2+1-4x-\left(4x^2+1\right)}{2x-1+\sqrt{4x^2+1}}$

Operiamo al numeratore:

$\displaystyle\lim_{x\to +\infty}\frac{4x^2+1-4x-4x^2-1}{2x-1+\sqrt{4x^2+1}}$

$\displaystyle\lim_{x \to +\infty}\frac{-4x}{2x-1+\sqrt{4x^2+1}}$

E, infine, calcoliamo il valore del limite all’infinito:

$\displaystyle\lim_{x \to +\infty} \cfrac{-4x }{2x-1 +\sqrt{4x^2+1} } = \cfrac{-4(+\infty) }{2(+\infty)+\sqrt{4(+\infty)^2} } = \cfrac{-\infty}{+\infty} =$

Anche se c’è una x al quadrato al denominatore, il suo grado in realtà è 1 perché è all’interno di una radice:

$\sqrt{4x^2} =\sqrt{4}\cdot \sqrt{x^2} = \sqrt{4}\cdot x^{2/2} =\sqrt{4} x^1=\sqrt{4}x .$

Pertanto il risultato dell’indeterminazione -∞/+∞ è la divisione dei coefficienti delle x di grado superiore, poiché il grado del numeratore è uguale al grado del denominatore.

$\displaystyle\lim_{x\to +\infty}\frac{-4x}{2x-1+\sqrt{4x^2+1} }=\frac{-\infty}{+\infty}=\frac{-4}{2+\sqrt{4}}=\frac{-4}{2+2}=\frac{-4}{4}=\bm{-1}$

Nota che poiché ci sono due termini di primo grado al denominatore

$\bigl(2x$

$\sqrt{4x^2}\bigr)$

, per risolvere l’indeterminazione -∞/+∞ occorre prendere tutti i coefficienti dei termini di primo grado, cioè i

$2$

$2x$

e il

$\sqrt{4}$

$\sqrt{4x^2}.$

Esercizio 7

Calcola il limite quando x tende a 1 della seguente funzione con frazioni:

$\displaystyle\lim_{x\to 1}\left(\frac{1}{1-x}-\frac{3}{1-x^3}\right)$

vedi soluzione

Cercando di fare il limite, otteniamo il limite indeterminato di infinito meno infinito:

$\displaystyle\lim_{x\to 1}\left(\frac{1}{1-x}-\frac{3}{1-x^3}\right)=\frac{1}{1-1}--\frac{3}{1-1^3}=\frac{1}{0}-\frac{3}{0}=\bm{\infty-\infty}$

Dobbiamo quindi ridurre le frazioni ad un denominatore comune, o in altre parole dobbiamo moltiplicare il numeratore e il denominatore di una frazione per il denominatore dell’altra:

$\begin{array}{l}\displaystyle\lim_{x \to 1}\left(\frac{1}{1-x}-\frac{3}{1-x^3} \right)=\\[5ex]\displaystyle =\lim_{x\to 1}\left( \frac{1\cdot(1-x^3)}{(1-x)\cdot(1-x^3)}-\frac{3\cdot(1-x)}{(1-x^3)\cdot(1-x)}\right)=\\[5ex]\displaystyle =\lim_{x \to 1}\left(\frac{1-x^3}{1-x-x^3+x^4}-\frac{3-3x}{1-x-x^3+x^4}\right)\end{array}$

E poiché le due frazioni ora hanno lo stesso denominatore, possiamo metterle insieme:

$\displaystyle\lim_{x \to 1}\left(\frac{1-x^3}{1-x-x^3+x^4}-\frac{3-3x}{1-x-x^3+x^4}\right)=\lim_{x\to 1}\frac{1-x^3-(3-3x)}{1-x-x^3+x^4}$

Operiamo:

$\displaystyle\lim_{x \to 1} \cfrac{1-x^3-3+3x}{1-x-x^3+x^4}$

$\displaystyle\lim_{x \to 1} \cfrac{-x^3+3x-2}{x^4-x^3-x+1}$

E proviamo di nuovo a risolvere il limite:

$\displaystyle\lim_{x \to 1}\frac{-x^3+3x-2}{x^4-x^3-x+1}=\frac{-1^3+3\cdot1-2}{1^4-1^3-1+1}=\mathbf{\frac{0}{0}}$

Ma troviamo l’indeterminazione zero divisa per zero. Dobbiamo quindi fattorizzare i polinomi del numeratore e del denominatore:

$\displaystyle\lim_{x \to 1}\frac{-x^3+3x-2}{x^4-x^3-x+1}=\lim_{x \to 1}\frac{-(x-1)^2(x+2)}{(x-1)^2(x^2+x+1)}$

Ora semplifichiamo la frazione rimuovendo il fattore che si ripete al numeratore e al denominatore:

$\displaystyle\lim_{x \to 1}\frac{-\cancel{(x-1)^2}(x+2)}{\cancel{(x-1)^2}(x^2+x+1)}=\lim_{x \to 1}\frac{-(x+2)}{x^2+x+1}$

E, infine, risolviamo il limite:

$\displaystyle\lim_{x \to 1}\frac{-(x+2)}{x^2+x+1}=\frac{-(1+2)}{1^2+1+1}=\frac{-3}{3}=\bm{-1}$

Risolvere l’indeterminazione infinito meno infinito

Infinito meno infinita indeterminazione nelle funzioni polinomiali

Indeterminazione infinito meno infinito con le frazioni

indeterminazione infinito meno infinito con radici

Risolti problemi di indeterminazione infinita meno infinita

Esercizio 1

Esercizio 2

Esercizio 3

Esercizio 4

Esercizio 5

Esercizio 6

Esercizio 7

Lascia un commento Annulla risposta