Indeterminatezza infinita tra l'infinito (∞/∞)

In questo articolo spieghiamo come calcolare l’infinito dell’indeterminazione tra l’infinito (∞/∞). Troverai esempi di questa indeterminazione con tutti i tipi di funzioni: funzioni polinomiali, radicali, esponenziali, ecc. Inoltre potrai allenarti con esercizi risolti passo dopo passo di limiti che danno infinite indeterminazioni tra gli infiniti.

Come risolvere l’indeterminatezza infinita tra infiniti

Quando il limite di una funzione dà infinito diviso infinito, significa che si tratta di un’indeterminazione (o forma indeterminata). Per risolvere il limite di una funzione che dà infinito di indeterminazione tra infinito, è necessario confrontare il grado del polinomio al numeratore con il grado del polinomio al denominatore.

$\displaystyle\lim_{x\to +\infty}\frac{a_nx^r+a_{n-1}x^{r-1}+a_{n-2}x^{r-2}+\dots}{b_nx^s+b_{n-1}x^{s-1}+b_{n-2}x^{s-2}+\dots}=\frac{+\infty}{+\infty}$

Il risultato dell’indeterminazione infinito diviso per infinito dipende dal grado del numeratore e dal grado del denominatore della frazione:

Se il grado del polinomio del numeratore è inferiore al grado del polinomio del denominatore, l’infinito dell’indeterminazione diviso per infinito è uguale a zero.
Se il grado del polinomio del numeratore è equivalente al grado del polinomio del denominatore, l’indeterminazione infinita su infinito è il quoziente dei coefficienti principali dei due polinomi.
Se il grado del polinomio del numeratore è maggiore del grado del polinomio del denominatore, l’infinito dell’indeterminazione tra gli infiniti dà più o meno infinito (il segno dipende dai termini principali dei due polinomi).

$\displaystyle \lim_{x \to \pm \infty}}\frac{a_nx^r+a_{n-1}x^{r-1}+a_{n-2}x^{r-2}+\dots}{b_nx^s+b_{n-1}x^{s-1}+b_{n-2}x^{s-2}+\dots}=\left\{ \begin{array}{lcl} 0 & \text{si} & r<s \\[3ex]="" \cfrac{a_n}{b_n}="" &="" \text{si}="" r="s" \\[5ex]="" \pm="" \infty="">s \end{array}\right.” title=”Rendered by QuickLaTeX.com” height=”139″ width=”767″ style=”vertical-align: 0px;”> <h2 class=$ Esempi di infinite indeterminazioni tra l’infinito

Vediamo come viene risolta la forma indeterminata infinito tra infinito osservando diversi esempi di ciascun caso:

grado del numeratore minore del grado del denominatore

Come abbiamo visto sopra, quando il grado del polinomio del numeratore è inferiore al grado del polinomio del denominatore, il limite indeterminato infinito tra l’infinito dà sempre 0.

Esempio 1:

$\displaystyle \lim_{x \to +\infty} \cfrac{6x^2-5}{x^3+1} = \cfrac{6(+\infty)^2}{(+\infty)^3} = \cfrac{+\infty}{+\infty}= \bm{0}$

Il polinomio del numeratore è di secondo grado, mentre quello del denominatore è di terzo grado, quindi la soluzione del limite è 0.

Esempio 2:

$\displaystyle \lim_{x \to -\infty} \frac{-7x}{2x^4+3x^2}=\frac{-7\cdot (-\infty)}{2(-\infty)^4}=\frac{+\infty}{+\infty}= \bm{0}$

La funzione polinomiale del numeratore è di primo grado, ma la funzione del denominatore è di quarto grado, quindi il limite all’infinito negativo è 0.

grado del numeratore uguale al grado del denominatore

Quando il grado del polinomio del numeratore è uguale al grado del polinomio del denominatore, il limite indeterminato infinito per infinito viene calcolato dividendo i coefficienti principali (coefficiente del termine di grado superiore) dei due polinomi.

Esempio 3:

$\displaystyle \lim_{x \to +\infty} \cfrac{4x^2+1}{2x^2-5} = \cfrac{4(+\infty)^2}{2(+\infty)^2}= \cfrac{+\infty}{+\infty} =\cfrac{4}{2} = \bm{2}$

In questo caso i due polinomi sono di secondo grado, è quindi necessario dividere i coefficienti dei termini di grado superiore per trovare il limite all’infinito positivo.

Esempio 4:

$\displaystyle \lim_{x \to -\infty} \cfrac{2x+1}{5x+3} = \cfrac{2(-\infty)}{5(-\infty)}= \cfrac{-\infty}{-\infty} =\cfrac{\bm{2}}{\bm{5}}$

Sebbene il limite sia quando x tende a meno infinito, l’infinita indeterminazione tra l’infinito si risolve allo stesso modo.

Grado del numeratore maggiore del grado del denominatore

Quando il grado del polinomio del numeratore è maggiore del grado del polinomio del denominatore, la forma indeterminata dell’infinito tra infiniti darà sempre infinito, e il segno dell’infinito è determinato dai termini di grado superiore dei due polinomi.

Esempio 5:

$\displaystyle \lim_{x \to +\infty} \cfrac{x^2+7}{x-2} = \cfrac{(+\infty)^2}{+\infty} = \cfrac{+\infty}{+\infty} = \bm{+\infty}$

La funzione del numeratore ha grado maggiore di quella del denominatore, quindi l’indeterminazione infinito su infinito dà infinito. Inoltre, in questo caso sia il numeratore che il denominatore ottengono infinito positivo, quindi anche il risultato del limite deve essere positivo.

Esempio 6:

$\displaystyle \lim_{x \to -\infty} \cfrac{3x^2+2x-5}{7x+1} = \cfrac{3(-\infty)^2}{7(-\infty)}=\cfrac{3(+\infty)}{-\infty}}= \cfrac{+\infty}{-\infty}= \bm{-\infty}$

In questo problema, dal numeratore si ottiene un infinito positivo perché qualsiasi termine al quadrato è positivo, mentre dal denominatore si ottiene un infinito negativo. Pertanto, il limite risultante è negativo perché positivo diviso per negativo è uguale a negativo.

Infinita indeterminatezza tra l’infinito con radici

Abbiamo appena visto come calcolare l’indeterminatezza infinita tra l’infinito quando abbiamo funzioni polinomiali. Ma… quanto fa l’infinito diviso per l’infinito se abbiamo radici?

Il grado di una funzione irrazionale (funzione con radici) è il quoziente tra il grado del termine principale e l’indice del radicale.

$\sqrt[\color{red}\bm{m}\color{black}]{a_nx^{\color{blue}\bm{n}\color{black}}+a_{n-1}x^{n-1}+a_{n-2}x^{n-2}+\dots} \ \longrightarrow \ \text{grado}=\cfrac{\color{blue}\bm{n}\color{black}}{\color{red}\bm{m}\color{black}}$

Pertanto, se il limite di una funzione con radici dà l’indeterminazione tra infinito , dobbiamo applicare le stesse regole spiegate sopra per i gradi del numeratore e del denominatore, tenendo però conto che il grado di un polinomio con radici si calcola diversamente.

Guarda il seguente esempio del limite all’infinito di una funzione con radicali:

$\displaystyle\lim_{x\to +\infty}\frac{4x^2+11}{\sqrt{x^8-3x^2-5}}=\frac{4(+\infty)^2}{\sqrt{(+\infty)^8}}=\frac{+\infty}{+\infty}=\bm{0}$

Il grado del numeratore è 2 e il grado del denominatore è 4 (8/2=4), quindi il limite è 0 perché il grado del numeratore è inferiore al grado del denominatore.

Se invece il grado del numeratore e quello del denominatore sono uguali, per calcolare il limite indeterminato dobbiamo prendere il coefficiente principale con il radicale:

$\displaystyle\lim_{x\to +\infty}\frac{6x-5}{\sqrt{9x^2+2x}}=\frac{6(+\infty)}{\sqrt{9(+\infty)^2}}=\frac{+\infty}{+\infty}=\frac{6}{\sqrt{9}}=\frac{6}{3}=\bm{2}$

Indeterminazione infinita tra infinito con funzioni esponenziali

Non ci resta infine che studiare un caso del quoziente di indeterminazione degli infiniti: quanto vale l’infinita indeterminazione tra infinito e funzioni esponenziali.

La crescita di una funzione esponenziale è molto maggiore della crescita di una funzione polinomiale, quindi dobbiamo considerare che il grado di una funzione esponenziale è maggiore del grado di una funzione polinomiale.

$\text{exponencial}>\text{polinomio}” title=”Rendered by QuickLaTeX.com” height=”16″ width=”192″ style=”vertical-align: -4px;”> Pertanto, se l’indeterminazione infinita divisa per infinito risulta da un limite con funzioni esponenziali, è sufficiente applicare le stesse regole spiegate per i gradi del numeratore e del denominatore, tenendo però conto che una funzione esponenziale è di ordine superiore a un polinomio. . Inoltre, se abbiamo funzioni esponenziali al numeratore e al denominatore della divisione, la funzione esponenziale con la base più grande sarà di ordine superiore. <p class=$ $\displaystyle\lim_{x\to +\infty}\frac{7x^5+6x^3-4x}{4^x}=\frac{7(+\infty)^5}{4^{+\infty}}=\frac{+\infty}{+\infty}=\bm{0}$

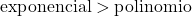
In questo caso il denominatore è formato da una funzione esponenziale, quindi è di ordine superiore al numeratore. Dunque la forma indeterminata dell’infinito tra l’infinito svanisce.

Esercizi risolti di infinita indeterminatezza tra l’infinito

Esercizio 1

Calcolare il limite della seguente funzione razionale:

$\displaystyle\lim_{x \to +\infty} \cfrac{6x-5}{x^2-1}$

vedi soluzione

Nel calcolare il limite, otteniamo l’infinita indeterminazione tra l’infinito, ma poiché il grado del numeratore è inferiore al grado del denominatore, il limite indeterminato è uguale a zero.

$\displaystyle \lim_{x \to +\infty} \cfrac{6x-5}{x^2-1} = \cfrac{6(+\infty)}{(+\infty)^2} = \cfrac{+\infty}{+\infty}= \bm{0}$

Esercizio 2

Risolvi il seguente limite indeterminato:

$\displaystyle\lim_{x \to +\infty} \cfrac{x^3+4x-1}{5x^2-3x+4}$

vedi soluzione

Quando si tenta di calcolare il limite, si ottiene l’indeterminazione ∞/∞. In questo caso, il grado del polinomio del numeratore è maggiore del grado del polinomio del denominatore, quindi il limite indeterminato è uguale a più infinito.

$\displaystyle \lim_{x \to +\infty} \cfrac{x^3+4x-1}{5x^2-3x+4} = \cfrac{(+\infty)^3}{5(+\infty)^2} = \cfrac{+\infty}{+\infty}= \bm{+\infty}$

Esercizio 3

Risolvi il seguente limite all’infinito:

$\displaystyle \lim_{x \to +\infty} \cfrac{-4x^2+3}{3x+1}$

vedi soluzione

Il limite dà l’indeterminazione meno infinito tra più infinito. Il grado del numeratore è maggiore del grado del denominatore, quindi il limite indeterminato è uguale a più infinito. Tuttavia, poiché la divisione è infinito negativo per infinito positivo, il risultato è meno infinito.

$\displaystyle \lim_{x \to +\infty} \cfrac{-4x^2+3}{3x+1} = \cfrac{-4(+\infty)^2}{3(+\infty)} =\cfrac{-4(+\infty)}{+\infty}= \cfrac{-\infty}{+\infty}= \bm{-\infty}$

Esercizio 4

Risolvi il seguente limite indeterminato:

$\displaystyle \lim_{x \to +\infty} \cfrac{5x+8}{-5x+2}$

vedi soluzione

In questo problema la forma infinita indeterminata su infinito si ottiene dal quoziente di due polinomi dello stesso grado, quindi il risultato del limite indeterminato è la divisione dei loro coefficienti principali:

$\displaystyle \lim_{x \to +\infty} \cfrac{5x+8}{-5x+2} = \cfrac{5(+\infty)}{-5(+\infty)} = \cfrac{+\infty}{-\infty}=\cfrac{5}{-5}= \bm{-1}$

Esercizio 5

Calcolare almeno all’infinito il seguente limite:

$\displaystyle \lim_{x \to -\infty} \cfrac{x^2+3x+5}{x^4-x-6}$

vedi soluzione

Il grado dell’espressione algebrica del numeratore è inferiore al grado dell’espressione del denominatore, quindi l’indeterminazione +∞/+∞ dà 0:

$\displaystyle \lim_{x \to -\infty} \cfrac{x^2+3x+5}{x^4-x-6} = \cfrac{(-\infty)^2}{(-\infty)^4} = \cfrac{+\infty}{+\infty}= \bm{0}$

Esercizio 6

Risolvi il seguente limite indeterminato di una funzione con radici:

$\displaystyle\lim_{x\to +\infty}\frac{\sqrt[3]{x^7-4x^3}}{x^2+5x}$

vedi soluzione

L’espressione del numeratore è sotto un radicale, quindi il suo grado è 7/3. D’altra parte, il polinomio al denominatore è quadratico. E poiché 7/3>2, il limite dà più infinito:

$\displaystyle \lim_{x \to +\infty}\frac{\sqrt[3]{x^7-4x^3}}{x^2+5x}=\frac{\sqrt[3]{(+\infty)^7}}{(+\infty)^2}=\frac{+\infty}{+\infty}=+\infty$

Esercizio 7

Determina il limite all’infinito della seguente funzione con le frazioni:

$\displaystyle\lim_{x \to +\infty} \cfrac{-2x^2}{5-4x}$

vedi soluzione

In questo esercizio l’indeterminazione meno infinito diviso meno infinito si ottiene con il grado del numeratore maggiore del grado del denominatore, quindi:

$\displaystyle \lim_{x \to +\infty} \cfrac{-2x^2}{5-4x} = \cfrac{-2(+\infty)^2}{-4(+\infty)} = \cfrac{-2(+\infty)}{-\infty}= \cfrac{-\infty}{-\infty} =\bm{+\infty}$

Esercizio 8

Trovare il limite almeno all’infinito della seguente funzione:

$\displaystyle \lim_{x \to -\infty} \cfrac{9x}{4-x^2}$

vedi soluzione

Il polinomio al denominatore è quadratico, mentre il polinomio al numeratore è lineare. Pertanto, l’infinito di indeterminatezza diviso per infinito dà 0.

$\displaystyle \lim_{x \to -\infty} \cfrac{9x}{4-x^2} = \cfrac{9(-\infty)}{-(-\infty)^2} = \cfrac{-\infty}{-(+\infty)}=\cfrac{-\infty}{-\infty}= \bm{0}$

Esercizio 9

Risolvi il limite almeno infinito della seguente funzione:

$\displaystyle \lim_{x \to -\infty} \cfrac{-2x^3-3x}{-3x^2+4x-1}$

vedi soluzione

Il numeratore è di grado maggiore del denominatore, quindi il risultato della forma indeterminata ∞/∞ sarà infinito. Inoltre, il segno dell’infinito sarà negativo perché il positivo diviso per il negativo dà il negativo:

$\displaystyle \lim_{x \to -\infty} \cfrac{-2x^3-3x}{-3x^2+4x-1} = \cfrac{-2(-\infty)^3}{-3(-\infty)^2} =\cfrac{-2(-\infty)}{-3(+\infty)}= \cfrac{+\infty}{-\infty}= \bm{-\infty}$

Esercizio 10

Risolvi il seguente limite con indeterminazione infinita tra infinito:

$\displaystyle\lim_{x \to +\infty}\cfrac{2^x-4}{-2x^6+x^4}$

vedi soluzione

La funzione esponenziale è di ordine superiore rispetto alla funzione polinomiale, quindi il limite darà infinito. Tuttavia, dividendo il positivo per il negativo, il segno dell’infinito sarà negativo:

$\displaystyle\lim_{x \to +\infty}\frac{2^x-4}{-2x^6+x^4}=\frac{2^{+\infty}}{-2(+\infty)^6}=\frac{+\infty}{-\infty}=\bm{-\infty}$

Esercizio 11

Calcolare il seguente limite:

$\displaystyle \lim_{x \to -\infty} \cfrac{x^3-5x}{-x^3-5x^2}$

vedi soluzione

In questo problema l’indeterminazione infinito su infinito si risolve dividendo i coefficienti dominanti dei due polinomi, poiché sono dello stesso grado:

$\displaystyle \lim_{x \to -\infty} \cfrac{x^3-5x}{-x^3-5x^2} = \cfrac{(-\infty)^3}{-(-\infty)^3} = \cfrac{-\infty}{-(-\infty)}= \cfrac{-\infty}{+\infty}=\cfrac{1}{-1}=\bm{-1}$

Esercizio 12

Risolvi il limite della seguente funzione quando x tende all’infinito:

$\displaystyle \lim_{x \to +\infty} \cfrac{(x+3)^2}{x}$

vedi soluzione

Sebbene l’incognita al numeratore non sia direttamente al quadrato, risolvendo l’identità notevole possiamo vedere chiaramente che il grado del numeratore è maggiore del grado del denominatore. Ancora:

$\displaystyle \lim_{x \to +\infty} \cfrac{(x+3)^2}{x}=\lim_{x \to +\infty} \cfrac{x^2+9+6x}{x} = \cfrac{(+\infty)^2}{+\infty} = \cfrac{+\infty}{+\infty} = \bm{+\infty}$

Esercizio 13

Calcola il limite all’infinito della seguente funzione con radice cubica:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[3]{8x^3+1}}{-4x}$

vedi soluzione

Il numeratore è formato da una radice cubica, quindi il suo grado è 3/3=1. Allora, il grado del numeratore è uguale a quello del denominatore, quindi l’infinita indeterminazione tra infinito si risolve come segue:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[3]{8x^3+1}}{-4x}= \cfrac{\sqrt[3]{8(+\infty)^3}}{-4(\infty)}= \cfrac{+\infty}{-\infty} = \cfrac{\sqrt[3]{8}}{-4}=\cfrac{2}{-4}=\bm{-}\mathbf{\cfrac{1}{2}}$

Esercizio 14

Risolvi il limite all’infinito della seguente funzione con due radicali:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[3]{6x^7+2x^3}}{\sqrt{x^5-3x^4+2x}}$

vedi soluzione

Il grado del numeratore è 7/3 = 2,33 e il grado del denominatore è 5/2 = 2,5. Pertanto, poiché il grado del numeratore è inferiore al grado del denominatore, il limite infinito indeterminato tra l’infinito è 0:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[3]{6x^7+2x^3}}{\sqrt{x^5-3x^4+2x}}=\cfrac{\sqrt[3]{6(+\infty)^7}}{\sqrt{(+\infty)^5}}=\cfrac{+\infty}{+\infty}=\bm{0}$

Esercizio 15

Calcolare il seguente limite:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[5]{x^7-2x^5-1}}{4^{x-2}+3x}$

vedi soluzione

Indipendentemente dal grado del numeratore, poiché abbiamo una funzione esponenziale al denominatore, il risultato della forma indeterminata infinito su infinito è 0:

$\displaystyle \lim_{x \to +\infty} \cfrac{\sqrt[5]{x^7-2x^5-1}}{4^{x-2}+3x}=\cfrac{\sqrt[5]{(+\infty)^7}}{4^{+\infty-2}}=\cfrac{+\infty}{+\infty}=\bm{0}$

Indeterminazione infinita tra l'infinito (∞/∞)

Come risolvere l’indeterminatezza infinita tra infiniti

grado del numeratore minore del grado del denominatore

Esempio 1:

Esempio 2:

grado del numeratore uguale al grado del denominatore

Esempio 3:

Esempio 4:

Grado del numeratore maggiore del grado del denominatore

Esempio 5:

Esempio 6:

Infinita indeterminatezza tra l’infinito con radici

Indeterminazione infinita tra infinito con funzioni esponenziali

Esercizi risolti di infinita indeterminatezza tra l’infinito

Esercizio 1

Esercizio 2

Esercizio 3

Esercizio 4

Esercizio 5

Esercizio 6

Esercizio 7

Esercizio 8

Esercizio 9

Esercizio 10

Esercizio 11

Esercizio 12

Esercizio 13

Esercizio 14

Esercizio 15

Lascia un commento Annulla risposta