Identità notevoli (o prodotti notevoli) -

Qui troverai la spiegazione della risoluzione di tutti i tipi di identità notevoli (o prodotti notevoli). Potrai vedere quali sono le formule di tutte le identità notevoli, oltre ad esempi ed esercizi risolti passo dopo passo. Inoltre, ti mostreremo a cosa servono queste famose regole matematiche.

👉👉 Di seguito spieghiamo passo dopo passo ogni identità notevole, ma se preferisci puoi andare direttamente alla tabella 😉 dove sono riassunte tutte le formule . 👈👈

Cosa sono le identità notevoli (o i prodotti notevoli)?

Le identità notevoli , chiamate anche prodotti notevoli o uguaglianze notevoli , sono regole matematiche che consentono di risolvere direttamente operazioni con polinomi.

Le formule di identità degne di nota più comuni sono il quadrato di una somma , il quadrato di una differenza (o sottrazione) e la somma per la differenza .

identità o uguaglianze notevoli del prodotto

Ma di seguito non solo ti insegneremo come calcolare questi prodotti notevoli, ma ti mostreremo anche tutti i tipi di identità notevoli che esistono.

Formule di identità notevoli (o prodotti)

Una volta che abbiamo visto la definizione di prodotti notevoli (o uguaglianze notevoli), vedremo quali sono le formule per le identità notevoli. Se invece sei interessato alle demo delle formule, puoi visualizzarle facendo clic sui pulsanti “visualizza demo”.

quadrato di una somma

Il quadrato di una somma , o somma al quadrato , è una delle identità più importanti. Più precisamente si tratta di un binomio con due termini positivi elevato a 2, cioè la sua espressione algebrica è (a+b) ² .

Quindi la formula per il quadrato di una somma è:

identità notevoli al quadrato con una somma

Guarda la dimostrazione della formula

Se partiamo da un binomio positivo elevato a 2:

$(a+b)^2$

Matematicamente, il quadrato sopra equivale al fattore

$(a+b)$

moltiplicato per se stesso:

$(a+b)^2=(a+b)\cdot (a+b)$

Quindi moltiplichiamo i polinomi utilizzando la proprietà distributiva:

$\begin{aligned} (a+b)\cdot (a+b) & = a\cdot a +a\cdot b +b\cdot a +b\cdot b \\[2ex] &=a^2+ab+ba+b^2 \end{aligned}$

Dei quattro termini ottenuti,

$ab$

$ba$

sembrano simili, quindi possiamo raggrupparli:

$a^2+ab+ba+b^2 = a^2+2ab+b^2$

Tanto che siamo già arrivati all’espressione della formula della somma al quadrato, da cui si ricava:

$(a+b)^2= a^2+2ab+b^2$

Per curiosità, lo sviluppo espressivo di questo tipo di prodotto straordinario è chiamato trinomio quadrato perfetto.

Quindi il quadrato di una somma è uguale al quadrato del primo termine, più il doppio del prodotto del primo per il secondo, più il quadrato del secondo.

Quindi per risolvere una somma quadrata non è sufficiente elevare ciascuna addizione ad entrambe, ma, in più, le due addizioni devono essere moltiplicate tra loro e per 2. È importante ricordarlo perché un errore molto tipico di questo tipo di prodotto È notevole dimenticare questo termine.

identità polinomiali e binomiali notevoli

Esempio:

Calcola la seguente identità notevole applicando la formula corrispondente:

$(x+5)^2$

Come abbiamo appena visto, la formula per l’uguaglianza notevole di una somma al quadrato è:

$(a+b)^2=a^2+2ab+b^2$

Pertanto, dobbiamo prima identificare i parametri

$a$

$b$

della formula. In questo caso,

$a$

rappresenta il

$x$

della coppia e

$b$

corrisponde al numero 5:

$\left. \begin{array}{l} (a+b)^2\\[2ex] (x+5)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=5 \end{array}$

Quindi, ora che conosciamo i valori di

$a$

e di

$b,$

possiamo usare la formula per un binomio positivo quadrato per trovare il risultato:

quadrato di una differenza

Il quadrato di una differenza , o differenza al quadrato , è un’altra delle 3 identità notevoli più utilizzate. In particolare, corrisponde ad un binomio formato da un termine positivo e da un altro termine negativo elevato a 2, vale a dire che la sua espressione algebrica è (ab) ² .

Quindi, la formula per il quadrato di una differenza (o quadrato di una sottrazione) è la seguente:

Guarda la demo della formula

Dall’espressione binomiale di una sottrazione al quadrato:

$(a-b)^2$

Ovviamente la potenza precedente è uguale al prodotto del fattore

$(a-b)$

moltiplicato per se stesso:

$(a-b)^2= (a-b)\cdot (a-b)$

Ora moltiplichiamo le due parentesi applicando la proprietà distributiva:

$\begin{aligned}(a-b)\cdot (a-b) & = a\cdot a +a\cdot (-b) - b\cdot a - b \cdot (-b) \\[2ex] & = a^2-ab-ba+b^2 \end{aligned}$

Quindi devi solo raggruppare insieme i termini simili per completare il controllo della formula:

$a^2-ab-ba+b^2 = a^2-2ab +b^2$

Quindi la formula per il quadrato di una differenza viene dimostrata matematicamente:

$(a-b)^2=a^2-2ab+b^2$

Quindi il quadrato di una differenza è uguale al quadrato del primo termine, meno il doppio del prodotto del primo per il secondo, più il quadrato del secondo.

Per quanto riguarda la notevole uguaglianza della somma al quadrato, non dobbiamo dimenticare di inserire il termine medio della formula, poiché la seguente equazione non è corretta:

Esempio:

Risolvi la seguente uguaglianza notevole di una differenza al quadrato:

$(x-3)^2$

È il prodotto notevole di una sottrazione al quadrato, occorre quindi applicare la formula corrispondente:

$(a-b)^2=a^2-2ab+b^2$

Successivamente, dobbiamo identificare quali sono i valori delle incognite.

$a$

$b$

della formula. In questo caso,

$a$

è la variabile

$x$

$b$

corrisponde al numero 3:

$\left. \begin{array}{l} (a-b)^2\\[2ex] (x-3)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=3 \end{array}$

Si noti che il segno negativo non fa parte del parametro

$b,$

ma devi sempre prendere il numero senza segno per applicare correttamente questa formula.

Conosciamo quindi già i valori di

$a$

e di

$b$

, è quindi sufficiente sostituire questi valori nella formula per risolvere l’identità notevole:

esempi ed esercizi risolti passo dopo passo di uguaglianze notevoli

somma per differenza

Il prodotto di una somma per una differenza è una delle 3 identità notevoli più utilizzate. Come suggerisce il nome, si tratta di un binomio positivo moltiplicato per il suo binomio coniugato (stesso binomio ma cambiato il segno intermedio), vale a dire che l’espressione algebrica di questo tipo di prodotto notevole è (a +b) · (ab) .

La formula per l’identità notevole del prodotto di una somma per una differenza è la seguente:

identità, prodotti e uguaglianze notevoli delle scuole superiori 2, 3 e 4 che

Guarda la dimostrazione della formula

Partendo dal prodotto di una somma per la sottrazione di due termini qualsiasi:

$(a+b)\cdot (a-b)$

Per dimostrare la formula, dobbiamo semplicemente moltiplicare la prima parentesi per la seconda parentesi utilizzando la proprietà distributiva:

$\begin{array}{l}(a+b)\cdot (a-b)= \\[2ex] = a\cdot a +a\cdot (-b) +b \cdot a +b\cdot (-b) =\\[2ex] = a^2 -ab+ba-b^2\end{array}$

Ora raggruppiamo insieme termini simili:

$a^2 -ab+ba-b^2=a^2-b^2$

E abbiamo così raggiunto l’espressione di una notevole uguaglianza. Così viene dimostrata la formula per questo notevole tipo di identità:

$(a+b)\cdot (a-b) =a^2-b^2$

Pertanto, il prodotto della somma per la differenza di due quantità è uguale alla differenza dei quadrati di queste quantità. O in altre parole, moltiplicare la somma di due termini diversi sottraendo gli stessi due termini equivale a elevare al quadrato ciascuno dei 2 termini e sottrarli.

Esempio:

Trovare, utilizzando la formula corrispondente, il seguente prodotto notevole della somma per la differenza di due termini diversi:

$(x+2)\cdot (x-2)$

Come abbiamo visto sopra, la formula per l’uguaglianza notevole di una somma moltiplicata per una differenza è la seguente:

$(a+b)\cdot (a-b) =a^2-b^2$

Innanzitutto quello che dobbiamo fare è identificare i valori delle lettere

$a$

$b$

della formula. In questo caso

$a$

corrispondono alla variabile

$x$

$b$

corrisponde al numero 2.

$\left. \begin{array}{l} (a+b)\cdot (a-b) \\[2ex] (x+2)\cdot (x-2) \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=2 \end{array}$

E quando sappiamo già quali valori assumono i parametri

$a$

$b,$

Applichiamo la formula del prodotto della somma per la differenza:

quadrato di un trinomio

Il quadrato di un trinomio (polinomio formato da 3 termini) è uguale al quadrato del primo termine, più il quadrato del secondo termine, più il quadrato del terzo termine, più il doppio del primo per il secondo, più il doppio del primo per il terzo, più il doppio del secondo per il terzo.

Quali sono le formule per tutte le identità, i prodotti o le uguaglianze notevoli?

Guarda la demo della formula

Da qualsiasi trinomio al quadrato:

$(a+b+c)^2$

Il quadrato sopra può essere scomposto nel trinomio moltiplicato per se stesso:

$(a+b+c)^2 = (a+b+c)(a+b+c)$

Ora risolviamo la moltiplicazione polinomiale:

$(a+b+c)(a+b+c)= a^2+ab+ac+ba+b^2+bc+ca+cb+c^2$

E infine, raggruppiamo termini simili:

$a^2+ab+ac+ba+b^2+bc+ca+cb+c^2 = a^2+b^2+c^2+2ab+2ac+2bc$

In questo modo siamo già arrivati all’espressione della formula, quindi è dimostrata la formula per il quadrato di un trinomio:

$(a+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc$

Esempio:

Trova la seguente uguaglianza notevole:

$\left(x^2+x+3\right)^2$

La formula del quadrato di un trinomio è:

$(a+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc$

Come in tutte le uguaglianze notevoli, bisogna prima individuare i valori delle incognite presenti nella formula. In questo esercizio

$a$

Est

$x^2,$

il coefficiente

$b$

corrispondono a

$x,$

$c$

è il termine indipendente 3:

$\left. \begin{array}{c} (a+b+c)^2\\[2ex] \left(x^2+x+3\right)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x^2 \\[2ex] b=x \\[2ex] c=3 \end{array}$

E quando conosciamo già i valori, sostituiamo semplicemente questi valori nella formula ed eseguiamo i calcoli:

calcolatore di identità, prodotti e uguaglianze notevoli

Identità (o prodotti) notevoli al cubo

Abbiamo appena studiato tutte le identità notevoli al quadrato, cioè tutti i tipi di identità notevoli che sono formate da potenze elevate a 2. Bene, ora analizzeremo le identità notevoli al cubo. Naturalmente, le formule di identità al cubo sono un po’ più complicate, ma sono anche molto utili.

cubo di una somma

Il notevole prodotto cubico di una somma è un binomio (polinomio con solo due monomi) elevato a 3 i cui due elementi sono positivi. Pertanto, algebricamente, il cubo di una somma è espresso come (a+b) ³ .

La formula per l’uguaglianza notevole del cubo di una somma è:

Quali sono tutti i prodotti, le identità o i legami degni di nota?

Guarda la dimostrazione della formula

Partendo da un binomio positivo al cubo:

$(a+b)^3$

La potenza di cui sopra può essere fattorizzata nel prodotto del fattore

$(a+b)$

dal suo quadrato:

$(a+b)^3=(a+b)\cdot (a+b)^2$

Allo stesso modo, come abbiamo visto nelle uguaglianze quadrate notevoli, il binomio

$(a+b)$

Può essere risolto con la formula del quadrato di una somma:

$(a+b)\cdot (a+b)^2=(a+b)\cdot (a^2+2ab+b^2)$

Quindi moltiplichiamo i due polinomi tra loro:

$\begin{aligned} (a+b)\cdot (a^2+2ab+b^2) & = a\cdot a^2 +a\cdot 2ab + a\cdot b^2+b\cdot a^2 +b\cdot 2ab +b \cdot b^2 \\[2ex] & = a^3+2a^2b+ab^2+ba^2+2ab^2+b^3 \end{aligned}$

Infine, non ci resta che raggruppare insieme termini simili:

$a^3+2a^2b+ab^2+ba^2+2ab^2+b^3 = a^3+3a^2b+3ab^2+b^3$

E così è verificata la formula per l’identità notevole di una somma binomia al cubo:

$(a+b)^3 = a^3+3a^2b+3ab^2 +b^3$

In breve, una somma elevata a 3 è uguale al cubo della prima, più tre volte il quadrato della prima per la seconda, più tre volte la prima per il quadrato della seconda, più il cubo della seconda.

Esempio:

Risolvi la seguente identità notevole di una somma cubica utilizzando la formula corrispondente:

$(x+2)^3$

In questo problema abbiamo un binomio elevato a 3 i cui due termini sono positivi. Dobbiamo quindi utilizzare la formula per una somma al cubo:

$(a+b)^3 = a^3+3a^2b+3ab^2 +b^3$

Ora dobbiamo trovare il valore dei parametri

$a$

$b$

della formula. In questo caso,

$a$

corrispondono alla variabile

$x$

$b$

è il numero 2.

$\left. \begin{array}{l} (a+b)^3\\[2ex] (x+2)^3 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=2 \end{array}$

Con cui calcoliamo il prodotto notevole sostituendo i valori di

$a$

e di

$b$

nella formula:

10 esempi di prodotti o identità degne di nota

cubo di differenza

Il cubo di differenza , o cubo di sottrazione , è un binomio elevato a 3 che ha un termine con segno negativo. Quindi, l’espressione matematica per questo straordinario tipo di prodotto è (ab) ³ .

La formula per il cubo di una differenza (o sottrazione) è:

identità cubiche, prodotti o uguaglianze notevoli

Guarda la dimostrazione della formula

Ovviamente la dimostrazione di questa formula è molto simile a quella del prodotto notevole di una somma al cubo. Ma in questo caso partiamo da un binomio al cubo negativo:

$(a-b)^3$

Chiaramente il potenziamento precedente può essere scomposto nel prodotto del fattore

$(a-b)$

moltiplicato per il suo quadrato:

$(a-b)^3=(a-b)\cdot (a-b)^2$

Quindi, come abbiamo studiato nelle identità quadrate notevoli, il binomio

$(a-b)$

Può essere calcolato con la formula del quadrato di una differenza:

$(a-b)\cdot (a-b)^2=(a-b)\cdot (a^2-2ab+b^2)$

Produciamo ora il prodotto dei due polinomi:

$\begin{aligned} (a-b)\cdot (a^2-2ab+b^2) & = a\cdot a^2 +a\cdot (-2ab) + a\cdot b^2-b\cdot a^2 -b\cdot (-2ab)-b \cdot b^2 \\[2ex] & = a^3-2a^2b+ab^2-ba^2+2ab^2-b^3 \end{aligned}$

E l’ultimo passaggio è raggruppare termini simili:

$a^3-2a^2b+ab^2-ba^2+2ab^2-b^3 = a^3-3a^2b+3ab^2-b^3$

Si verifica così la formula per l’identità notevole di un binomio sottratto elevato al cubo:

$(a-b)^3 = a^3-3a^2b+3ab^2-b^3$

Quindi una differenza (o sottrazione) elevata a tre è uguale al cubo della prima, meno tre volte il quadrato della prima per la seconda, più tre volte la prima per il quadrato della seconda, meno il cubo della seconda.

Esempio:

Calcola il successivo binomio al cubo (differenza) utilizzando la formula corrispondente:

$(3x-2)^3$

In questo esercizio abbiamo una coppia con un elemento positivo e un elemento negativo. Dobbiamo quindi utilizzare la formula per la differenza al cubo:

$(a-b)^3 = a^3-3a^2b+3ab^2 -b^3$

Innanzitutto, come sempre, identifichiamo il valore delle incognite

$a$

$b$

della formula. In questo caso

$a$

rappresenta il monomio

$3x$

$b$

è il termine indipendente del binomio, cioè 2.

$\left. \begin{array}{l} (a-b)^3\\[2ex] (3x-2)^3 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=3x \\[2ex] b=2 \end{array}$

Si noti che il parametro

$b$

è semplicemente uguale a 2, senza il segno negativo del numero. È importante tenerlo presente per applicare correttamente la formula.

Infine, troviamo la notevole identità mettendo i valori di

$a$

e di

$b$

nella formula:

sviluppare identità, prodotti e uguaglianze notevoli

Tabella riassuntiva delle identità notevoli

In sintesi, abbiamo creato una tabella con tutte le identità (o prodotti) notevoli che abbiamo visto, così sarà più facile per te studiarli. 😉

formule di identità o uguaglianze di prodotti notevoli

Esercizi risolti di identità notevoli (o prodotti)

Affinché tu possa comprendere meglio la nozione di identità notevoli, chiamate anche prodotti notevoli o uguaglianze notevoli, abbiamo preparato diversi esercizi risolti passo dopo passo. Puoi provare a farli e poi verificare se sei andato bene con le soluzioni degli esercizi.

⬇⬇ Non dimenticare che puoi farci tutte le tue domande qui sotto nei commenti! ⬇⬇

Esercizio 1

Espandi le seguenti identità notevoli (quadrati somma):

$\text{A)} \ (x+3)^2$

$\text{B)} \ (6x+2)^2$

$\text{C)} \ \left(x^2+7\right)^2$

$\text{D)} \ (5x+8y)^2$

vedi soluzione

Tutte le identità notevoli nel problema sono somme quadrate, quindi in questo caso dobbiamo applicare sempre la stessa formula:

$(a+b)^2=a^2+2ab+b^2$

$\text{A)} \ \begin{aligned}(x+3)^2& =x^2+2\cdot x\cdot 3 +3^2\\[2ex] & = \bm{x^2+6x +9}\end{aligned}$

$\text{B)} \ \begin{aligned}(6x+2)^2 & =(6x)^2+2\cdot 6x \cdot 2+2^2\\[2ex] & = \bm{36x^2+24x+4}\end{aligned}$

$\text{C)} \ \begin{aligned}\left(x^2+7\right)^2 & = \left(x^2\right)^2+2\cdot x^2\cdot 7 +7^2\\[2ex] & = \bm{x^4+14x^2 +49}\end{aligned}$

$\text{D)} \ \begin{aligned}(5x+8y)^2 & =(5x)^2+2\cdot 5x\cdot 8y +(8y)^2\\[2ex] & = \bm{25x^2+80xy+64y^2}\end{aligned}$

Esercizio 2

Sviluppa i seguenti prodotti degni di nota (differenze al quadrato):

$\text{A)} \ (x-2)^2$

$\text{B)} \ (3-7x)^2$

$\text{C)} \ \left(x^2-6\right)^2$

$\text{D)} \ (-3x+y)^2$

vedi soluzione

Tutti i prodotti degni di nota in questo esercizio sono sottrazioni quadrate, quindi dobbiamo applicare solo una formula:

$(a-b)^2=a^2-2ab+b^2$

$\text{A)} \ \begin{aligned}(x-2)^2& =x^2-2\cdot x\cdot 2 +2^2\\[2ex] & = \bm{x^2-4x +4}\end{aligned}$

$\text{B)} \ \begin{aligned}(3-7x)^2 & =3^2-2\cdot 3\cdot 7x +(7x)^2\\[2ex] & = \bm{9-42x+49x^2}\end{aligned}$

$\text{C)} \ \begin{aligned}\left(x^2-6\right)^2 & = \left(x^2\right)^2-2\cdot x^2\cdot 6 +6^2\\[2ex] & = \bm{x^4-12x^2 +36}\end{aligned}$

$\text{D)} \ \begin{aligned}(-3x+y)^2 & = (y-3x)^2 \\[2ex] & = y^2-2\cdot y\cdot 3x +(3x)^2\\[2ex] & = \bm{y^2-6yx+9x^2}\end{aligned}$

Esercizio 3

Sviluppa le seguenti uguaglianze notevoli (prodotti di somme per differenze):

$\text{A)} \ (x+5)(x-5)$

$\text{B)} \ (2x+6)(2x-6)$

$\text{C)} \ (x+7)(x-7)$

$\text{D)} \ (x-4y)(x+4y)$

vedi soluzione

Poiché tutte le uguaglianze notevoli in questo esercizio sono moltiplicazioni di somme per differenze, vengono tutte risolte con la stessa formula:

$(a+b)\cdot (a-b) =a^2-b^2$

$\text{A)} \ \begin{aligned}(x+5)(x-5) &=x^2-5^2\\[2ex] & = \bm{x^2-25}\end{aligned}$

$\text{B)} \ \begin{aligned}(2x+6)(2x-6) & =(2x)^2-6^2 \\[2ex] & = \bm{4x^2-36}\end{aligned}$

$\text{C)} \ \begin{aligned}(x+7)(x-7) & =x^2-7^2 \\[2ex] & = \bm{x^2-49}\end{aligned}$

$\text{D)} \ \begin{aligned}(x-4y)(x+4y) & =(x+4y)(x-4y) \\[2ex] & =x^2-(4y)^2\\[2ex] & = \bm{x^2-16y^2}\end{aligned}$

Esercizio 4

Risolvi tutte le seguenti identità importanti:

$\text{A)} \ \left(x^2+10\right)\left(x^2-10\right)$

$\text{B)} \ \left(4x^2+2y^3\right)^2$

$\text{C)} \ \left(6x^3-4y^4\right)^2$

$\text{D)} \ \left(8x^3+y^2\right)\left(8x^3-y^2\right)$

$\text{E)} \ \left(5x^2-9x\right)^2$

vedi soluzione

$\text{A)} \ \begin{aligned}\left(x^2+10\right)\left(x^2-10\right) & =\left(x^2\right)^2-10^2\\[2ex] & = \bm{x^4-100}\end{aligned}$

$\text{B)} \ \begin{aligned}\left(4x^2+2y^3\right)^2 & =\left(4x^2\right)^2+2\cdot 4x^2\cdot 2y^3 +\left(2y^3\right)^2\\[2ex] & = \bm{16x^4+16x^2y^3+4y^6}\end{aligned}$

$\text{C)} \ \begin{aligned}\left(6x^3-4y^4\right)^2 & =\left(6x^3\right)^2-2\cdot 6x^3\cdot 4y^4 +\left(4y^4\right)^2 = \\[2ex] &= \bm{36x^6-48x^3y^4+16y^8}\end{aligned}$

$\text{D)} \ \begin{aligned}\left(8x^3+y^2\right)\left(8x^3-y^2\right) & =\left(8x^3\right)^2-\left(y^2\right)^2 \\[2ex] & = \bm{64x^6-y^4}\end{aligned}$

$\text{E)} \ \begin{aligned}\left(5x^2-9x\right)^2 & =\left(5x^2\right)^2-2\cdot 5x^2\cdot 9x +\left(9x\right)^2 \\[2ex] & = \bm{25x^4-90x^3+81x^2}\end{aligned}$

Esercizio 5

Calcolare i seguenti prodotti notevoli:

$\text{A)} \ (x+4)^3$

$\text{B)} \ \left(x^2-5\right)^3$

$\text{C)} \ \left(2x-1\right)^3$

$\text{D)} \ (5x+2)^3$

vedi soluzione

Per trovare tutti i prodotti notevoli del problema è necessario applicare le formule per una somma e una differenza al cubo a seconda dei casi:

$(a+b)^3 = a^3+3a^2b+3ab^2 +b^3$

$(a-b)^3 = a^3-3a^2b+3ab^2-b^3$

$\text{A)} \ \begin{aligned}(x+4)^3& =x^3+3\cdot x^2\cdot 4 +3\cdot x\cdot 4^2+4^3\\[2ex] & =x^3+3\cdot x^2\cdot 4 +3\cdot x\cdot 16+64 \\[2ex] & = \bm{x^3+12x^2+48x+64}\end{aligned}$

$\text{B)} \ \begin{aligned}\left(x^2-5\right)^3& =\left(x^2\right)^3-3\cdot \left(x^2\right)^2\cdot 5 +3\cdot x^2\cdot 5^2-5^3\\[2ex] & =x^6-3\cdot x^4\cdot 5 +3\cdot x^2\cdot 25-125 \\[2ex] & = \bm{x^6-15x^4+75x^2-125}\end{aligned}$

$\text{C)} \ \begin{aligned}\left(2x-1\right)^3& =\left(2x\right)^3-3\cdot \left(2x\right)^2\cdot 1 +3\cdot 2x\cdot 1^2-1^3\\[2ex] & =8x^3-3\cdot 4x^2\cdot 1 +3\cdot 2x\cdot 1-1 \\[2ex] & = \bm{8x^3-12x^2+6x-1}\end{aligned}$

$\text{D)} \ \begin{aligned}(5x+2)^3& =(5x)^3+3\cdot \left(5x\right)^2\cdot 2 +3\cdot 5x\cdot 2^2+2^3\\[2ex] & =125x^3+3\cdot 25x^2\cdot 2 +3\cdot 5x\cdot 4+8 \\[2ex] & = \bm{125x^3+150x^2+60x+8}\end{aligned}$

Esercizio 6

Risolvi le seguenti uguaglianze notevoli:

$\text{A)} \ \left(x^2+x+5\right)^2$

$\text{B)} \ \left(x^2+3x-4\right)^2$

$\text{C)} \ \left(4x^2-6x+3\right)^2$

$\text{D)} \ \left(x^3-3x^2-9x\right)^2$

vedi soluzione

Per risolvere tutte queste identità importanti, dobbiamo usare la formula per il quadrato di un trinomio, che è:

$(a+b+c)^2=a^2+b^2+c^2+2ab+2ac+2bc$

$\text{A)} \ \begin{array}{l} \left(x^2+x+5\right)^2 = \\[2ex] = \left(x^2\right)^2+x^2+5^2+2\cdot x^2 \cdot x + 2 \cdot x^2 \cdot 5 +2 \cdot x \cdot 5 = \\[2ex] = x^4+x^2+25+2x^3 + 10x^2 +10x = \\[2ex] = \bm{x^4+2x^3+11x^2+10x+25} \end{array}$

$\text{B)} \ \begin{array}{l}\left(x^2+3x-4\right)^2 = \\[2ex] = \left(x^2\right)^2+(3x)^2+(-4)^2+2\cdot x^2 \cdot 3x + 2 \cdot x^2 \cdot (-4) +2 \cdot 3x \cdot (-4) = \\[2ex] = x^4+9x^2+16+6x^3-8x^2-24x = \\[2ex] = \bm{x^4+6x^3+x^2-24x+16} \end{array}$

$\text{C)} \ \begin{array}{l}\left(4x^2-6x+3\right)^2 = \\[2ex] = \left(4x^2\right)^2+(-6x)^2+3^2+2\cdot 4x^2 \cdot (-6x) + 2 \cdot 4x^2 \cdot 3 +2 \cdot (-6x) \cdot 3 = \\[2ex] = 16x^4+36x^2+9-48x^3+24x^2-36x = \\[2ex] = \bm{16x^4-48x^3+60x^2-36x+9} \end{array}\end{array}$

$\text{D)} \ \begin{array}{l} \left(x^3-3x^2-9x\right)^2 = \\[2ex] = \left(x^3\right)^2+\left(-3x^2\right)^2+(-9x)^2+2\cdot x^3 \cdot (-3x^2) + 2 \cdot x^3 \cdot (-9x) +2 \cdot (-3x^2) \cdot (-9x) = \\[2ex] = x^6+9x^4+81x^2-6x^5-18x^4+54x^3 = \\[2ex] = \bm{x^6-6x^5-9x^4+54x^3+81x^2} \end{array}$

Esercizio 7

Calcola le seguenti identità notevoli con radici e frazioni (alta difficoltà):

$\text{A)} \ \displaystyle \left(\sqrt{2x}-\sqrt{8x}\right)^2$

$\text{B)} \ \displaystyle \left(\frac{1}{2}x^2+\frac{5}{3}x\right)\left(\frac{1}{2}x^2-\frac{5}{3}x\right)$

$\text{C)} \ \displaystyle \left(\frac{4}{3}x^2+\frac{3}{2}x\right)^2$

$\text{D)} \ \Bigl(9x^3+\sqrt{5x}\Bigr)\Bigl(9x^3-\sqrt{5x}\Bigr)$

vedi soluzione

La sezione A) consiste in una sottrazione al quadrato, per cui per risolverla occorre applicare la formula corrispondente e, inoltre, bisogna ricordare che se una radice è quadrata si semplifica:

$\text{A)} \ \begin{aligned}\left(\sqrt{2x}-\sqrt{8x}\right)^2 & =\left(\sqrt{2x}\right)^2-2\cdot \sqrt{2x}\cdot \sqrt{8x} +\left(\sqrt{8x}\right)^2\\[2ex] & =2x-2\sqrt{2x\cdot 8x} +8x \\[2ex] & = 10x-2\sqrt{16x^2} \\[2ex] &= 10x-2\cdot 4x = \\[2ex] & = 10x -8x \\[2ex] & = \bm{2x}\end{aligned}$

La sezione B) tratta dell’addizione per sottrazione e i monomi hanno coefficienti frazionari, con i quali questo notevole prodotto deve essere determinato utilizzando la formula dell’addizione per sottrazione e le proprietà delle frazioni:

$\text{B)} \ \begin{aligned}\displaystyle \left(\frac{1}{2}x^2+\frac{5}{3}x\right)\left(\frac{1}{2}x^2-\frac{5}{3}x\right) & \displaystyle =\left(\frac{1}{2}x^2\right)^2-\left(\frac{5}{3}x\right)^2\\[4ex] \displaystyle & =\frac{1^2}{2^2}x^4-\frac{5^2}{3^2}x^2\\[4ex]\displaystyle & = \mathbf{\frac{1}{4}}\bm{x^4-}\mathbf{\frac{25}{9}}\bm{x^2} \end{aligned}$

La notevole uguaglianza nella sezione C) è una somma elevata a 2 e, parimenti, è composta da frazioni. Pertanto, per calcolarlo dobbiamo utilizzare la formula della somma quadrata più le proprietà delle frazioni:

$\text{C)} \ \displaystyle \begin{aligned} \left(\frac{4}{3}x^2+\frac{3}{2}x\right)^2 & = \left(\frac{4}{3}x^2\right)^2+2\cdot \frac{4}{3}x^2\cdot \frac{3}{2}x +\left(\frac{3}{2}x\right)^2\\[2ex] & = \frac{4^2}{3^2}x^4+2\cdot \frac{12}{6}x^3 +\frac{3^2}{2^2}x^2 \\[2ex] &= \frac{16}{9}x^4 +2\cdot 2x^3+\frac{9}{4}x^2 \\[2ex] & = \mathbf{\frac{16}{9}} \bm{x^4+4x^3+}\mathbf{\frac{9}{4}}\bm{x^2}\end{aligned}$

L’ultima identità degna di nota riguarda una somma per una differenza con coefficienti irrazionali, quindi applichiamo la formula per una somma per una differenza e quindi semplifichiamo le radici quadrate:

$\text{D)} \ \begin{aligned}\Bigl(9x^3+\sqrt{5x}\Bigr)\Bigl(9x^3-\sqrt{5x}\Bigr) & =\Bigl(9x^3\Bigr)^2-\left(\sqrt{5x}\right)^2\\[2ex] & = \bm{81x^6-5x}\end{aligned}$

Altri tipi di identità notevoli

Tutte le identità importanti di cui abbiamo discusso sopra sono quelle più comunemente usate. Tuttavia, in matematica ci sono altri tipi di prodotti degni di nota che è interessante conoscere, poiché vengono utilizzati per scopi diversi.

somma di cubi

La somma dei cubi corrisponde a un binomio i cui due termini sono positivi e, inoltre, le sue radici cubiche sono esatte. Pertanto, l’espressione algebrica per una somma di cubi è a ³ +b ³ .

identità, prodotti o legami notevoli risolti

La formula di questo notevole prodotto viene utilizzata per fattorizzare un polinomio, ovvero attraverso la formula trasformiamo un polinomio in un prodotto di un binomio per un trinomio.

Quindi puoi vedere come è fatto, ecco un esempio di applicazione di questa straordinaria identità:

$x^3+8$

Infatti l’espressione precedente consiste in un’addizione di cubi perché radice cubica del monomio

$x^3$

è esatto (non fornisce un numero decimale) e anche il numero 8:

$\sqrt[3]{x^3} = x$

$\sqrt[3]{8} = 2$

$x^3+8=x^3+2^3$

Possiamo quindi utilizzare la formula della somma dei cubi perfetti per trasformare l’espressione cubica nel prodotto di un binomio per un trinomio:

$a^3+b^3 = (a+b)(a^2-ab+b^2)$

$\begin{aligned} x^3 +2^3 & = (x+2)(x^2-x \cdot 2 + 2^2) \\[2ex] & = (x+2)(x^2-2x + 4) \end{aligned}$

differenza di cubi

La differenza (o sottrazione) dei cubi è un binomio composto da un termine positivo e da un termine negativo le cui radici cubiche sono esatte. In altre parole, una differenza di cubi è espressa nella forma a ³ -b ³ .

Esercizi risolti per fattorizzare polinomi con identità notevoli

Facciamo un esempio per vedere come viene risolto questo notevole tipo di identità:

$x^3-27$

È una differenza di cubi perché entrambi hanno la radice cubica del monomio

$x^3$

poiché 27 sono corretti:

$\sqrt[3]{x^3} = x$

$\sqrt[3]{27} = 3$

$x^3-27=x^3-3^3$

Puoi quindi utilizzare la formula per la differenza dei cubi perfetti per fattorizzare il binomio:

$a^3-b^3 = (a-b)(a^2+ab+b^2)$

$\begin{aligned} x^3 -3^3 & = (x-3)(x^2+x \cdot 3 + 3^2) \\[2ex] & =(x-3)(x^2+3x + 9) \end{aligned}$

Prodotto di binomi con un termine comune

Questo prodotto notevole viene utilizzato per convertire un prodotto di due binomi che hanno un termine comune in un polinomio quadratico.

identità, prodotti o uguaglianze notevoli pdf

Ecco un esempio elaborato di questo tipo di prodotto straordinario:

$\begin{aligned} (x+4)(x+5) &= x^2+(4+5)x+4\cdot 5 \\[2ex] & = x^2+9x+20 \end{aligned}$

più identità

Sebbene le identità notevoli siano le più famose perché sono le più comuni, va notato che esistono più identità anche con altri nomi. Ecco un elenco di altre identità meno conosciute nel caso tu sia curioso:

Identità lagrangiane:

$(a^2+b^2)\cdot (x^2+y^2) =(ax+by)^2+(ay-bx)^2$
$(a^2-b^2)\cdot (x^2-y^2) =(ax+by)^2-(ay+bx)^2$

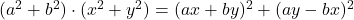
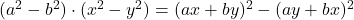
Identità di Legendre:

$(a+b)^2+(a-b)^2=2(a^2+b^2)$
$(a+b)^2-(a-b)^2=4ab$
$(a+b)^4-(a-b)^4=8ab(a^2+b^2)$

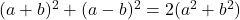
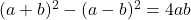
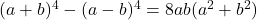
Identità di Argand:

$(x^2+x+1)(x^2-x+1) = x^4+x^2+1$

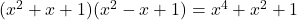
Identità gaussiane:

$a^3+b^3+c^3-3abc= (a+b+c)(a^2+b^2+c^2-ab-bc-ac)$
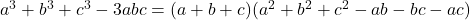
$a^3+b^3+c^3-3abc= \frac{1}{2} (a+b+c)\left[(a-b)^2+(b-c)^2+(a-c)^2\right]$

App di identità notevoli

Se sei arrivato fin qui, significa che sai già come eseguire calcoli con identità notevoli. Luminoso! Ma davvero… a cosa servono le identità notevoli? E quando vengono utilizzate le identità notevoli?

Come abbiamo visto in questo articolo, lo scopo principale delle identità notevoli è semplificare i calcoli. Vale a dire che grazie a prodotti notevoli possiamo risolvere direttamente alcune potenze di polinomi complessi senza dover effettuare operazioni difficili.

Ma le uguaglianze notevoli hanno anche altre funzioni, come la fattorizzazione dei polinomi e il completamento dei quadrati. Poi vedremo in cosa consiste ciascuna di queste applicazioni.

Fattorizzare i polinomi

Alcuni tipi molto specifici di polinomi possono essere fattorizzati con identità notevoli. Ad esempio, se troviamo un polinomio composto da due termini che sono quadrati perfetti (le loro radici quadrate sono esatte), possiamo fattorizzarlo utilizzando la formula di uguaglianza notevole del prodotto di una somma per una differenza:

$a^2-b^2 =(a+b)(a-b)$

$x^2-9 =(x+3)(x-3)$

Allo stesso modo, i trinomi che rispettano le identità notevoli del quadrato di un’addizione o di una sottrazione possono essere fattorizzati:

$a^2+2ab+b^2=(a+b)^2$

$x^2+4x+4=(x+2)^2$

$a^2-2ab+b^2=(a-b)^2$

$x^2-10x+25=(x-5)^2$

Allo stesso modo, una volta scomposto un polinomio, è possibile trovare le radici (o zeri) di quel polinomio. Anche così, questo concetto è un po’ più complicato da comprendere, quindi se sei più interessato, ti consigliamo di cercare la spiegazione nel motore di ricerca sul nostro sito (in alto a destra), poiché abbiamo un intero articolo che lo spiega.

completamento della piazza

Il completamento dei quadrati è una procedura matematica utilizzata per convertire un trinomio quadratico nella somma di un quadrato più (o meno) un numero.

Dato un qualsiasi trinomio:

$ax^2+bx+c$

Quindi il trinomio può essere trasformato nella seguente espressione:

$a(x+h)^2+k$

dove i parametri

$h$

$k$

vengono calcolati con le seguenti formule:

$h=\cfrac{b}{2a} \qquad \qquad k=c-ah^2$

Anche se non ti sembra, queste due formule sono desunte da identità illustri. Quindi, grazie ai notevoli prodotti, i quadrati possono essere completati.

Ad esempio, applicheremo questa procedura al seguente trinomio:

$2x^2+4x+3$

Calcoliamo i parametri

$h$

$k:$

$h=\cfrac{b}{2a}=\cfrac{4}{2\cdot 2} =1$

$k=c-ah^2 = 3-2\cdot 1^2 = 1$

E quindi il polinomio rimane:

$2(x+1)^2+1$

Cosa sono le identità notevoli (o i prodotti notevoli)?

Formule di identità notevoli (o prodotti)

quadrato di una somma

Esempio:

quadrato di una differenza

Esempio:

somma per differenza

Esempio:

quadrato di un trinomio

Esempio:

Identità (o prodotti) notevoli al cubo

cubo di una somma

Esempio:

cubo di differenza

Esempio:

Tabella riassuntiva delle identità notevoli

Esercizi risolti di identità notevoli (o prodotti)

Esercizio 1

Esercizio 2

Esercizio 3

Esercizio 4

Esercizio 5

Esercizio 6

Esercizio 7

Altri tipi di identità notevoli

somma di cubi

differenza di cubi

Prodotto di binomi con un termine comune

più identità

App di identità notevoli

Fattorizzare i polinomi

completamento della piazza

Lascia un commento Annulla risposta