In questa pagina troverai la spiegazione di cos’è un aereo, come si calcola e tutte le sue proprietà. Inoltre, potrai vedere esempi di piani, quali sono le posizioni relative tra due piani, come determinare l’angolo tra 2 piani e, infine, come esprimere numericamente qualsiasi piano utilizzando le equazioni del piano.
Cos’è un piano?
Nella geometria analitica, la definizione di piano è la seguente:
Un piano è un oggetto geometrico che ha due dimensioni (lunghezza e larghezza).
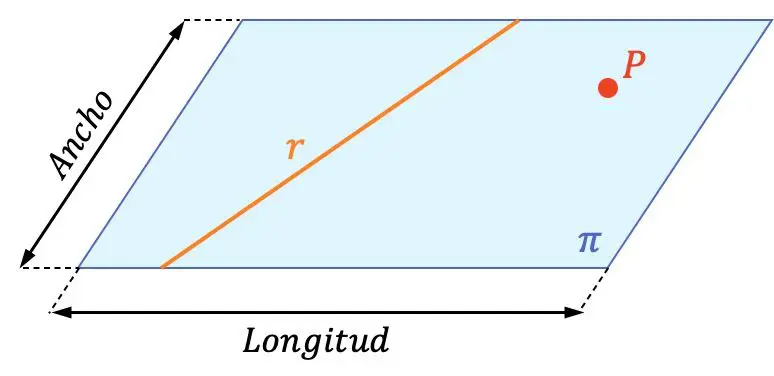
Pertanto un piano contiene infinite linee e infiniti punti. Nella rappresentazione grafica sopra puoi vedere la differenza tra un piano, una linea e un punto. Puoi anche verificare che la linea
![]()
e la mancia
![]()
sono contenuti nell’aereo
![]()
Come puoi vedere nel piano grafico, i piani sono solitamente denominati con lettere greche:
![]()
Un esempio di piano che usiamo molto in matematica è il piano cartesiano. Il piano cartesiano è il piano definito dall’asse delle ascisse (asse X) e dall’asse delle ordinate (asse Y). Uno degli usi del piano cartesiano è che viene utilizzato per descrivere la posizione di un oggetto in un sistema di riferimento.
Determinazione di un piano
Ora che abbiamo visto il significato di piano, vediamo come può essere determinato qualsiasi piano nello spazio tridimensionale (in R3).
Una pianta è interamente determinata dai seguenti elementi geometrici:
- Tre punti non allineati.
- Una linea retta e un punto esterno.
- Due rette parallele o due rette che si intersecano.
Per quanto riguarda l’ultimo punto, probabilmente già sai cosa significa che due rette sono parallele. Ma il significato delle linee secanti è meno conosciuto, quindi se hai qualche domanda qui, puoi controllare cosa sono le linee secanti .
Pertanto, se rispettiamo una delle 3 condizioni precedenti, significa che possiamo elaborare un piano.
proprietà del piano
Il piano risponde alle seguenti caratteristiche:
- Un piano contiene un’infinità di punti.
- Un piano contiene un’infinità di linee.
- Un piano è illimitato, cioè è una superficie che si estende nello spazio senza limiti.
- Due piani che si intersecano determinano una linea.
- Una linea che ha un punto in un piano non è necessariamente contenuta in esso. Affinché una linea faccia parte di un piano, deve avere almeno due punti nel piano.
- Infiniti piani attraversano una linea retta.
- Un semipiano è ciascuna delle 2 parti in cui si divide un piano quando viene tagliato da una delle sue linee.
equazioni piane
Nella geometria analitica, l’ equazione di un piano è un’equazione che consente di esprimere matematicamente qualsiasi piano. Quindi, per trovare l’equazione di un piano, hai solo bisogno di un punto e di due vettori linearmente indipendenti appartenenti a quel piano.

Tuttavia, come abbiamo visto in precedenza nella spiegazione del concetto di piano, esistono diversi modi per determinare un piano. Ebbene, allo stesso modo, ci sono anche diversi modi di esprimere analiticamente un piano.
Quindi tutti i tipi di equazioni del piano sono: l’ equazione vettoriale , le equazioni parametriche , l’ equazione implicita (o generale) e l’ equazione canonica (o segmentale) del piano.
Poi vedremo nel dettaglio la spiegazione e la formula di tutte le equazioni del piano.
Equazione vettoriale del piano
Consideriamo un punto e due vettori di direzione di un piano:
![Rendered by QuickLaTeX.com \begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cf5d4130501bb01b15aa80f8f80caf1a_l3.png)
La formula per l’equazione vettoriale di un piano è:
![]()
O equivalente:
![]()
Oro
![]()
E
![]()
sono due scalari, cioè due numeri reali.
Equazioni parametriche del piano
La formula per l’ equazione parametrica di un piano è:
![]()
Oro:
-
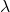
E
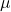
sono due scalari, cioè due numeri reali.
-
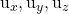
sono le componenti di uno dei due vettori guida del piano
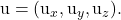
-
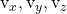
sono le componenti dell’altro vettore direttivo del piano
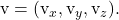
Equazione implicita o generale del piano
Consideriamo un punto e due vettori di direzione di un piano:
![Rendered by QuickLaTeX.com \begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-cf5d4130501bb01b15aa80f8f80caf1a_l3.png)
L’equazione implicita, generale o cartesiana di un piano si ottiene risolvendo il seguente determinante e ponendo il risultato uguale a 0:
![Rendered by QuickLaTeX.com \displaystyle \begin{vmatrix}\text{u}_x & \text{v}_x & x-P_x \\[1.1ex]\text{u}_y & \text{v}_y & y-P_y \\[1.1ex]\text{u}_z & \text{v}_z & z-P_z \end{vmatrix} = 0](https://mathority.org/wp-content/ql-cache/quicklatex.com-68d67612dfa54d76666aa37b702a472f_l3.png)
Pertanto, l’ equazione implicita o generale del piano risultante sarà la seguente:
![]()
Questo tipo di equazione piana è anche chiamata equazione piana cartesiana.
Equazione canonica o segmentale del piano
La formula per l’equazione canonica o segmentale di un piano è la seguente:
![]()
Oro:
-

è il punto di intersezione tra il piano e l’asse X.
-

è il punto di intersezione tra il piano e l’asse Y.
-

Qui è dove il piano interseca l’asse Z.
L’equazione canonica (o segmentale) del piano si può ricavare anche dalla sua equazione generale:
![]()
Innanzitutto, risolviamo il coefficiente D dall’equazione:
![]()
Quindi dividiamo l’intera equazione del piano per il valore del parametro D cambiato segno:
![]()
![]()
E, utilizzando le proprietà delle frazioni, arriviamo alla seguente espressione:
![]()
Da questa espressione deduciamo quindi le formule che permettono di calcolare direttamente i termini dell’equazione canonica o segmentaria di un piano:
![]()
di conseguenza, per poter formare questa variante delle equazioni del piano, i coefficienti A, B e C devono essere diversi da zero, evitando così indeterminazioni delle frazioni.
Posizione relativa di due piani
Nella geometria analitica ci sono solo tre possibili posizioni relative tra due piani: piani secanti, piani paralleli e piani coincidenti.
- Piani che si intersecano : due piani si intersecano se si intersecano solo su una linea.
- Piani paralleli : due piani sono paralleli se non si intersecano in nessun punto.
- Piani coincidenti : Due piani sono coincidenti se hanno tutti punti in comune.
piani che si intersecano

piani paralleli

piani coincidenti

Inoltre, se due piani che si intersecano si intersecano con un angolo di 90º, sono due piani reciprocamente perpendicolari .
Angolo tra due piani
L’angolo tra due piani è uguale all’angolo formato dai vettori normali di detti piani. Pertanto, per trovare l’angolo tra due piani, si calcola l’angolo formato dai loro vettori normali, poiché sono equivalenti.
Quindi, una volta che sappiamo esattamente in cosa consiste l’angolo tra due piani, vediamo la formula per calcolare l’angolo tra due piani nello spazio, che si deduce dalla formula dell’angolo tra due vettori:
Data l’equazione generale (o implicita) di due piani diversi:
![]()
![]()
Il vettore normale di ciascun piano è:
![]()
![]()
E l’angolo formato da questi due piani si determina calcolando l’angolo formato dai loro vettori normali utilizzando la seguente formula:
![]()
Ovviamente, una volta calcolato dalla formula il coseno dell’angolo formato dai due piani, dobbiamo invertire il coseno per trovare il valore di detto angolo.
Quando invece i due piani sono perpendicolari o paralleli, non è necessario applicare la formula, perché l’angolo tra i 2 piani può essere determinato direttamente:
- L’angolo tra due piani paralleli è 0º, poiché i loro vettori normali hanno la stessa direzione.
- L’angolo tra due piani perpendicolari è 90º, perché anche i loro vettori normali sono perpendicolari (o ortogonali) tra loro e quindi formano un angolo retto.