In questo articolo spieghiamo cosa sono le funzioni limitate (superiore e inferiore). Inoltre, ti mostreremo cosa significa per una funzione essere limitata in un punto e, infine, troverai le proprietà di questo tipo di funzione.
Cos’è una funzione limitata?
Una funzione limitata è una funzione il cui grafico è entro i limiti. Cioè, una funzione è limitata superiormente se esiste un numero K tale che non esiste alcun valore della funzione maggiore di K (f(x)≤K), e una funzione è limitata inferiormente se esiste un numero K tale che è minore di tutti i valori della funzione (f(x)≥K). Pertanto, una funzione limitata è una funzione limitata sopra e sotto.
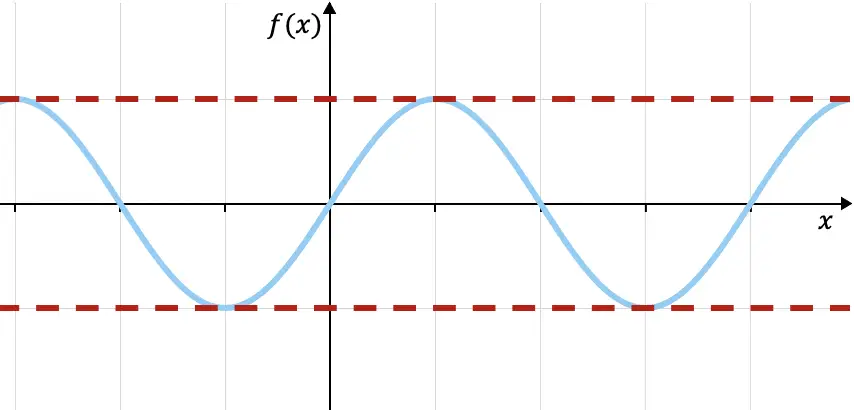
Ad esempio, la funzione seno trigonometrica, rappresentata graficamente sopra, è limitata in alto da f(x)=1 ed è limitata in basso da f(x)=-1 (linee tratteggiate rosse), poiché tutti i valori della funzione rientrano in questi due limiti. Puoi vedere più proprietà di questa funzione nel seguente link:
➤ Vedi: Caratteristiche della funzione seno
funzione delimitata sopra
Tuttavia, non tutte le funzioni sono limitate sopra e sotto, una funzione può essere limitata solo sopra o sotto.
Le funzioni limitate di cui sopra sono quelle che non superano un certo valore, ovvero è soddisfatta la seguente condizione:
![]()
dove il valore K è il limite superiore della funzione.
Ad esempio, la seguente parabola è limitata in alto da K=7, ma la funzione non è limitata in basso poiché i suoi rami si estendono all’infinito.

Logicamente, se la funzione è limitata da K=7, lo è anche da K=8 e valori superiori.
Il limite superiore più piccolo è chiamato limite superiore ed è rappresentato da sup(f) . Inoltre, se la funzione raggiunge tale limite superiore nel suo dominio, diremo che questo punto è il massimo assoluto della funzione.
➤ Vedi: quali sono i massimi e i minimi di una funzione?
Nel nostro caso la funzione è geometricamente limitata da K=7, è quindi l’estremo superiore e il massimo assoluto della funzione.
funzione delimitata di seguito
Le funzioni sotto delimitate sono quelle che non hanno un valore inferiore ad un certo numero, cioè soddisfano la seguente espressione matematica:
![]()
Dove il valore K è il limite inferiore della funzione.
Di seguito è riportata la rappresentazione grafica di una funzione esponenziale delimitata di seguito da K=3:

Ovviamente la funzione è limitata anche da valori inferiori a K=3.
Come prima, il limite inferiore più grande è chiamato limite inferiore ed è rappresentato da inf(f) . Inoltre, se la funzione raggiunge detto estremo inferiore nel suo dominio, diremo che questo punto è il minimo assoluto della funzione.
In questo caso K=3 non è il minimo assoluto della funzione, perché la funzione raggiunge questo valore all’infinito e, quindi, è fuori dal suo dominio. In altre parole, f(x)=3 è un asintoto orizzontale della funzione .
Esiste un teorema che permette di sapere se una funzione è limitata in alto e in basso senza la sua rappresentazione grafica. Clicca qui per vedere qual è il teorema di Weierstrass.
➤ Vedi: Teorema di Weierstrass
Funzione limitata in un punto
Abbiamo appena studiato la nozione di delimitazione di una funzione in generale, ma è anche possibile analizzare se una funzione è limitata o meno in un intorno più piccolo, cioè in una parte della funzione.
Sì
![]()
è un punto nel dominio della funzione e
![]()
qualsiasi valore, diremo che la funzione è limitata sopra/sotto in quel punto
![]()
se c’è un ambiente
![]()
dove la funzione è limitata sopra/sotto.
Pertanto una funzione è limitata nel punto
![]()
se è delimitato in alto e in basso in un quartiere
![]()
Ovviamente, se una funzione è limitata in generale, sarà limitata anche in ciascuno dei suoi punti. Ma è falso il contrario, cioè che una funzione può essere limitata in ciascuno dei suoi punti e non essere limitata in tutto il suo dominio.
Ad esempio, la seguente funzione affine è parzialmente limitata in ciascuno dei suoi punti, ma non è una funzione limitata.

Proprietà delle funzioni limitate
Le funzioni limitate hanno le seguenti proprietà:
- Sì

E

sono due funzioni limitate, l’addizione (o la sottrazione) delle due funzioni
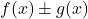
è anch’essa una funzione limitata.
- Sì

E

sono due funzioni limitate, il prodotto delle due funzioni
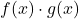
sembra anche essere una funzione limitata.
- Se una funzione ha un asintoto verticale non può essere totalmente limitata. D’altra parte, la funzione può essere limitata sopra o sotto.
- Qualsiasi funzione continua e limitata su un intervallo è integrabile.