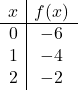Funzioni di valore assoluto -

Questa pagina spiega cos’è una funzione di valore assoluto. Imparerai anche come definire una funzione con valore assoluto a tratti e come rappresentare questi tipi di funzioni su un grafico. Inoltre lo vedrai con esempi di funzioni a valore assoluto e potrai esercitarti con esercizi e problemi risolti passo dopo passo.

Quali sono le funzioni con valore assoluto?

La definizione di una funzione valore assoluto è la seguente:

Il valore assoluto di una funzione trasforma tutte le sue immagini in immagini positive. Pertanto, il percorso di una funzione assoluta non può mai avere valori negativi.

La seguente funzione è un esempio di funzione valore assoluto:

$f(x)=\lvert 5x \rvert$

Se valutando la funzione in un punto otteniamo un risultato positivo, rimane positivo:

$f(1)=\lvert 5\cdot 1 \rvert =\lvert 5 \rvert = 5$

Se invece il risultato è negativo diventa positivo:

$f(-1)=\lvert 5\cdot (-1) \rvert =\lvert -5 \rvert = 5$

Le funzioni di valore assoluto vengono solitamente impartite alle scuole superiori, perché le loro caratteristiche le rendono un po’ difficili da comprendere.

Come definire a tratti una funzione con valore assoluto

Una funzione con valori assoluti può essere espressa come una funzione a tratti. Per fare ciò, devi cambiare il segno della funzione sugli intervalli che è negativo.

Vediamo un esempio di come passare da una funzione a valore assoluto a una funzione a tratti:

Esprimi la seguente funzione con un valore assoluto come funzione a tratti:

$f(x) = \lvert 4 - x^2 \rvert$

La prima cosa che dobbiamo fare è determinare quando la funzione è negativa. Per fare ciò impostiamo l’espressione algebrica in valore assoluto pari a 0 e risolviamo l’equazione:

$4-x^2=0$

$4 = x^2$

$\sqrt{4}=\sqrt{x^2}$

$\pm 2 = x$

$x=+2 \qquad x=-2$

Rappresentiamo ora i valori ottenuti sulla retta:

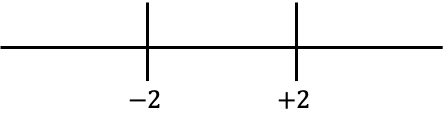
E guardiamo quale segno ha la funzione senza il valore assoluto in ogni intervallo della linea:

$x<-2$

Prendiamo ad esempio qualsiasi punto inferiore a -2

$x=-3:$

$4-(-3)^2$

$-5$

Negativo

$-2 < x < 2$

Prendiamo ad esempio qualsiasi punto compreso tra -2 e +2

$x=0:$

$4-0^2$

$+4$

Positivo

$x>2″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”42″ style=”vertical-align: -2px;”> Ad esempio, prendiamo qualsiasi punto maggiore di 2 <p class=$ $x=3:$

$4-3^2$

$-5$

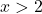
Negativo

Come abbiamo visto, la funzione senza il valore assoluto sarebbe negativa sugli intervalli

$x<-2$

$x>2.” title=”Rendered by QuickLaTeX.com” height=”14″ width=”47″ style=”vertical-align: -2px;”> Dobbiamo quindi esprimere la funzione in trattini cambiando il suo segno in questi intervalli: 2 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”97″ width=”372″ style=”vertical-align: 0px;”> 2 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”97″ width=”358″ style=”vertical-align: 0px;”> Nota che in alcuni intervalli devi includere l’uguaglianza. Ad esempio, qui lo inseriamo nel secondo intervallo <p class=$ $-2 \le x \le 2$

. Ma puoi posizionarlo in qualsiasi intervallo desideri purché vi sia un pareggio in tutti i punti critici. In altre parole, sarebbe lo stesso se avessimo definito la funzione come segue:

$\displaystyle f(x)= \lvert 4 - x^2 \rvert = \left\{ \begin{array}{lcl} -4+x^2 & \text{si} & x\le-2 \\[2ex] 4-x^2 & \text{si} & -2 < x < 2 \\[2ex] -4+x^2 & \text{si} & x\ge 2 \end{array} \right.$

Come rappresentare una funzione con valore assoluto

Per rappresentare una funzione con valore assoluto su un grafico, dobbiamo seguire i passaggi descritti di seguito:

Rappresentare la funzione come se non avesse valore assoluto.
Negli intervalli in cui la funzione è negativa, cioè si trova sotto l’asse X, disegna la funzione simmetrica.
Elimina la parte della funzione che si trova sotto l’asse X.

Vediamo un esempio di come rappresentare graficamente una funzione con valore assoluto

Rappresentare graficamente la seguente funzione in valore assoluto:

$f(x) = \lvert -x+2 \rvert$

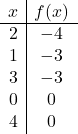
Per rappresentare una funzione con valore assoluto, dobbiamo prima rappresentare la funzione senza valore assoluto. Realizziamo quindi la tabella dei valori delle funzioni senza il valore assoluto:

$f(x)=-x+2$

$x= 0 \ \longrightarrow \ f(0) = -0+2=2$

$x= 1 \ \longrightarrow \ f(1) = -1+2=1$

$x= 2 \ \longrightarrow \ f(2) = -2+2=0$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 2 \\ 1 & 1 \\ 2 & 0 \end{array}$

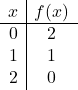
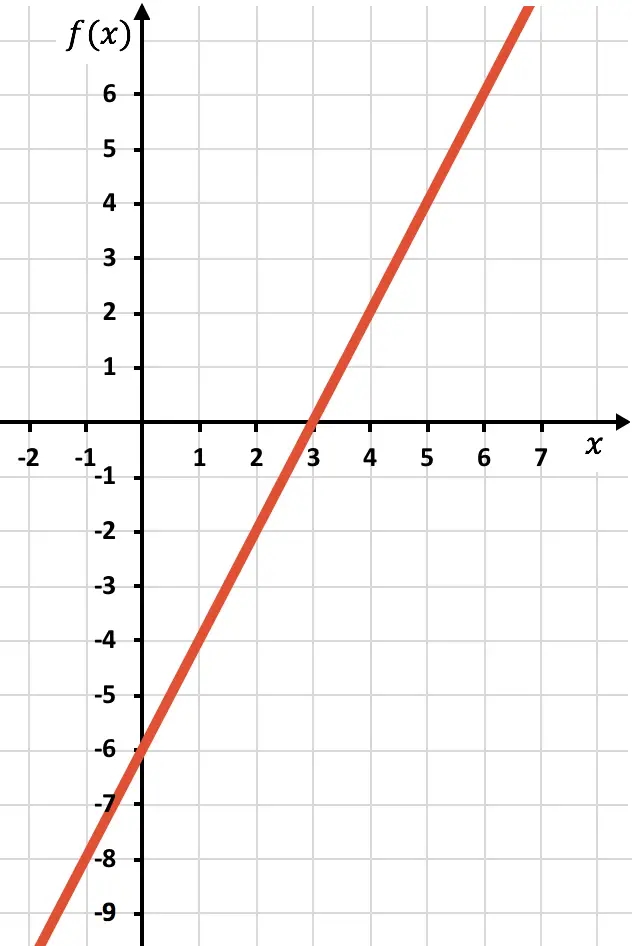
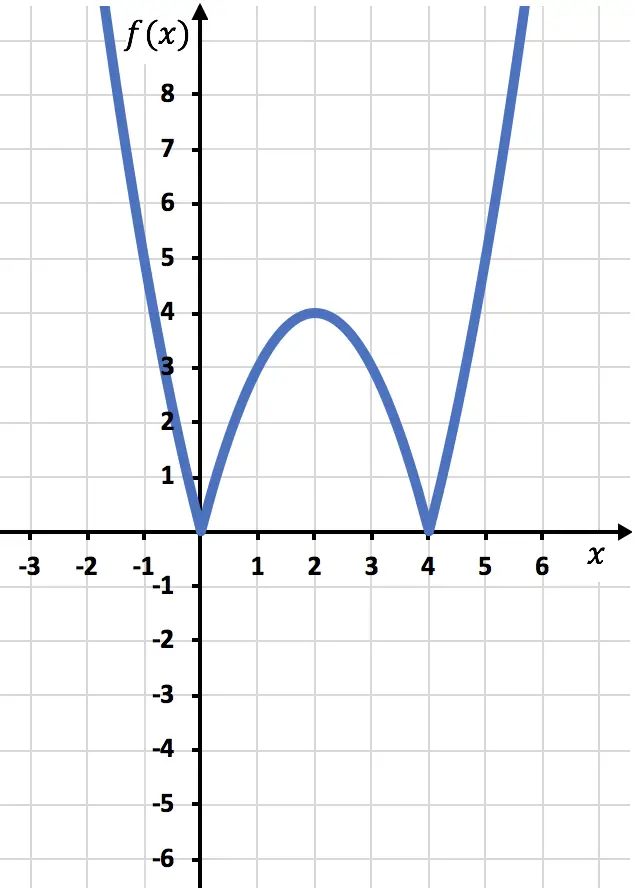
Rappresentiamo graficamente i punti e disegniamo la retta come se fosse una normale funzione:

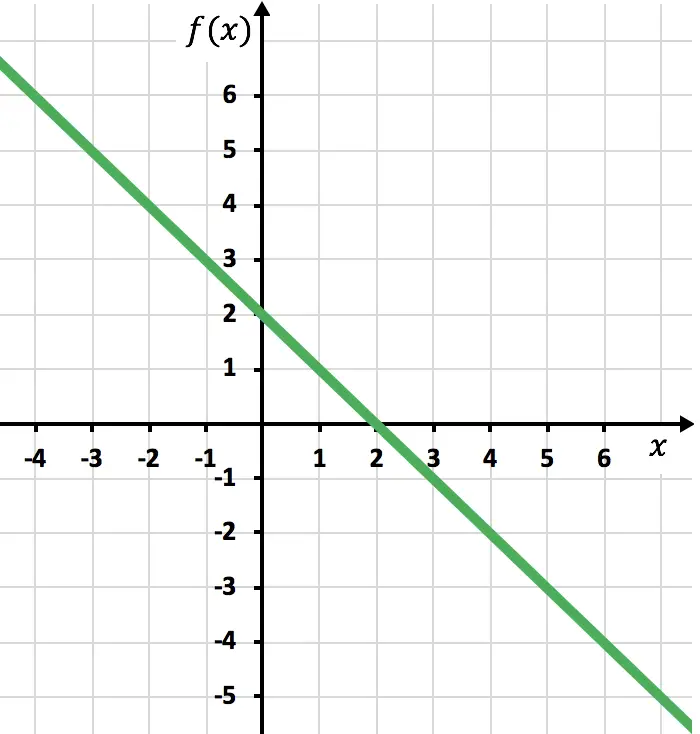
Ora dobbiamo disegnare la funzione simmetrica dove la funzione è negativa, cioè dove si trova sotto l’asse x. Invertiamo quindi la funzione partendo da x=2:

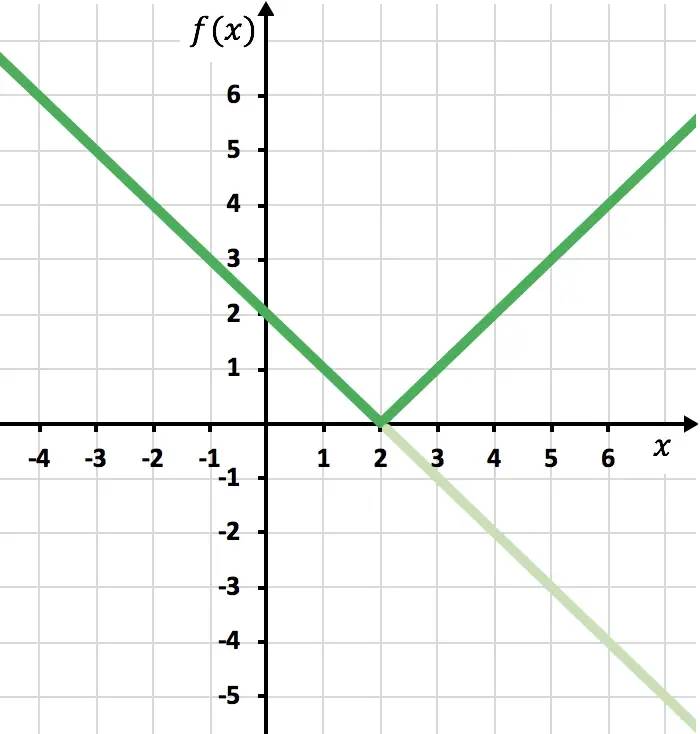
come rappresentare una funzione con valore assoluto

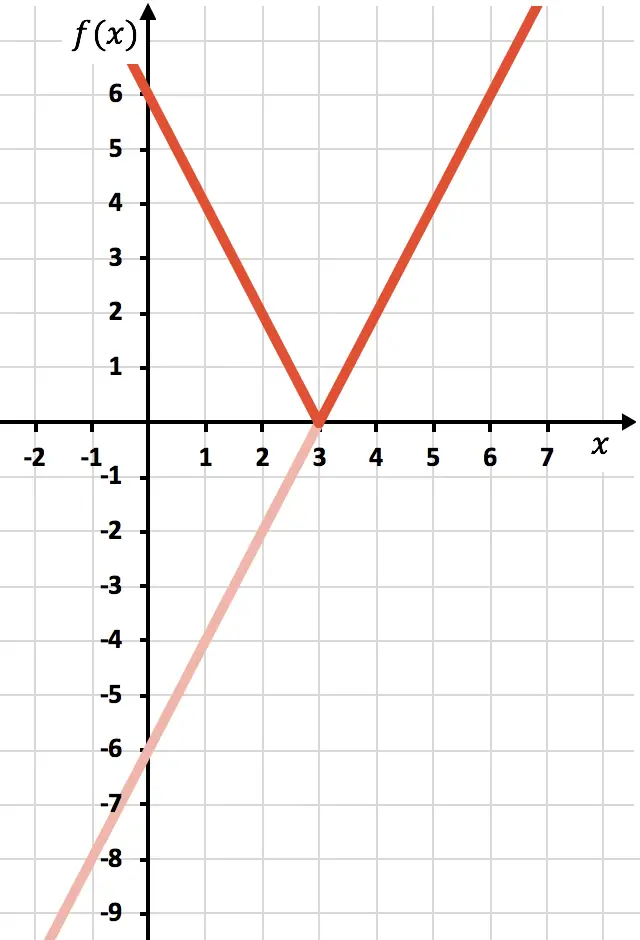
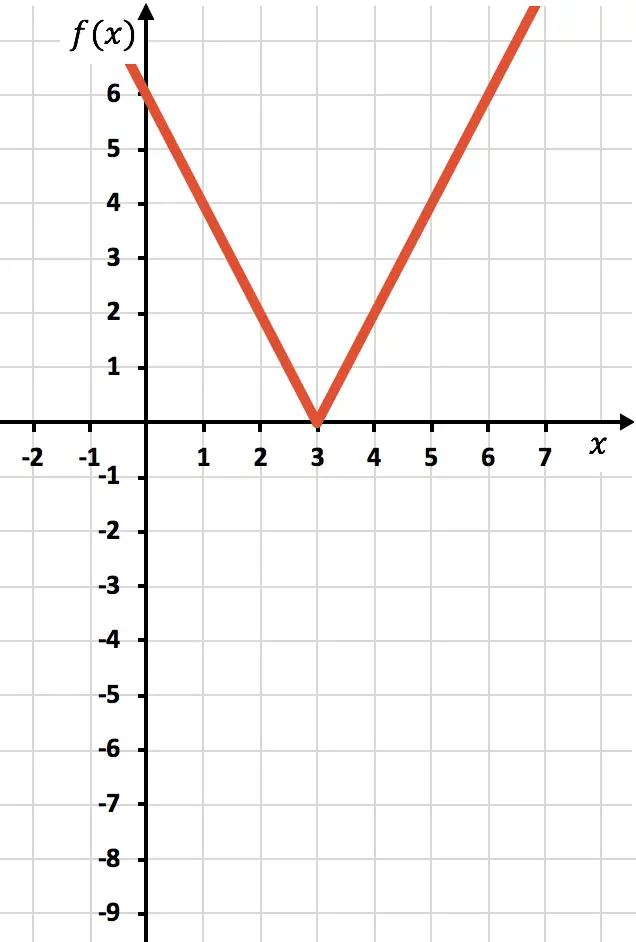
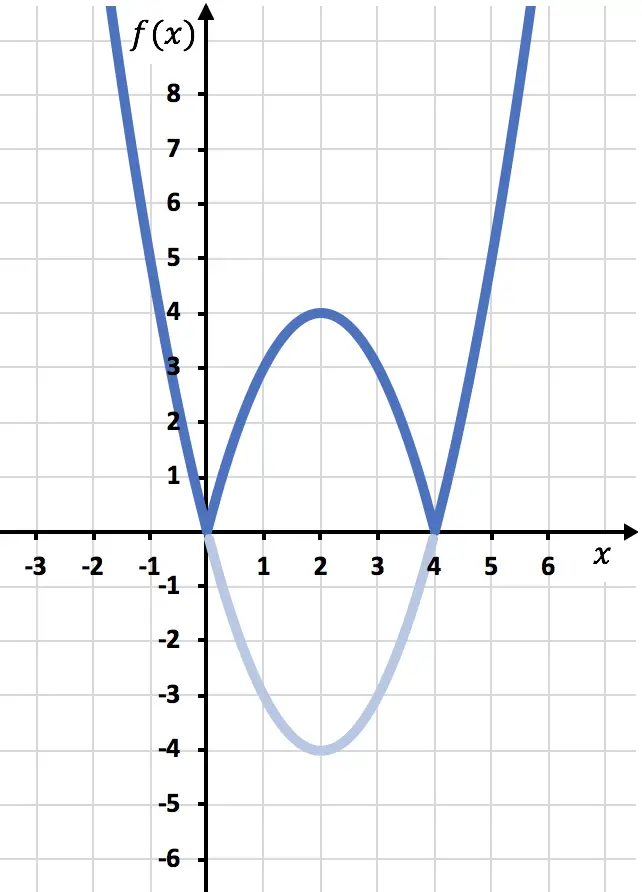
Ed infine eliminiamo la traccia della funzione che si trova sotto l’asse X:

come rappresentare graficamente una funzione con un valore assoluto

E in questo modo abbiamo già rappresentato la funzione con un valore assoluto. Come hai visto, l’unica cosa che cambia è che dobbiamo invertire la parte della funzione che si trova sotto l’asse OX. Pertanto, il grafico di qualsiasi funzione con valore assoluto si troverà sempre sul lato del semiasse Y positivo.

D’altra parte, ripassando i concetti, dal grafico possiamo dedurre che il dominio della precedente funzione valore assoluto è costituito interamente da numeri reali. D’altra parte, l’intervallo o intervallo di detta funzione con valore assoluto è composto solo da numeri positivi e zeri.

Esercizi risolti su funzioni a valore assoluto

Esercizio 1

Esprimi la seguente funzione con un valore assoluto come funzione a tratti:

$f(x)= \lvert -x+3 \rvert$

Vedi la soluzione

Prima di tutto dobbiamo considerare quando la funzione è negativa. Per fare ciò, impostiamo il valore assoluto uguale a zero e risolviamo l’equazione:

$-x+3=0$

$x=3$

Rappresentiamo il valore trovato sulla linea:

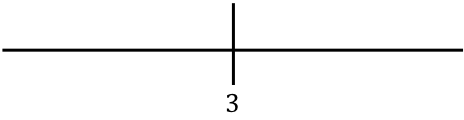
Adesso valutiamo un punto in ogni intervallo della funzione senza il valore assoluto per scoprire quale segno ha effettivamente la funzione in ogni tratto della retta:

$x<3$

Ad esempio, prendiamo qualsiasi punto inferiore a 3

$x=0:$

$-0+3$

$+3$

Positivo

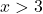$x>3″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”43″ style=”vertical-align: -2px;”> <p class=$ Ad esempio, prendiamo qualsiasi punto maggiore di 3

$x=4:$

$-4+3$

$-1$

Negativo

La funzione senza il valore assoluto sarebbe negativa nell’intervallo x>3. Dobbiamo quindi esprimere la funzione in trattini cambiandone il segno in questo intervallo:

$\displaystyle f(x)= \lvert -x+3 \rvert = \left\{ \begin{array}{lcl} -x+3 & \text{si} & x<3 \\[2ex] -(-x+3) & \text{si} & x\ge 3 \end{array} \right.$

$\displaystyle f(x)= \lvert -x+3 \rvert = \left\{ \begin{array}{lcl} -x+3 & \text{si} & x<3 \\[2ex] x-3 & \text{si} & x\ge 3 \end{array} \right.$

Esercizio 2

Trova l’espressione a tratti della seguente funzione con un valore assoluto:

$f(x)= \lvert 3x^2-75 \rvert$

Vedi la soluzione

La prima cosa che dobbiamo fare è determinare quando la funzione è negativa. Per fare ciò, dobbiamo impostare l’argomento del valore assoluto uguale a zero e risolvere l’equazione:

$3x^2-75 =0$

$3x^2=75$

$x^2=\cfrac{75}{3}$

$x^2=25$

$x= \pm 5$

Rappresentiamo ora le radici della funzione ottenuta a destra:

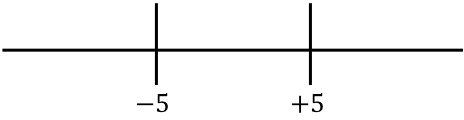
E guardiamo quale segno ha la funzione senza il valore assoluto in ogni intervallo della linea:

$x<-5$

Ad esempio, prendiamo qualsiasi punto inferiore a -5

$x=-6:$

$3(-6)^2-75$

$108-75$

$+33$

Positivo

$-5 < x < 5$

Prendiamo ad esempio qualsiasi punto compreso tra -5 e +5

$x=0:$

$3(0)^2-75$

$0-75$

$-75$

Negativo

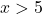$x>5″ title=”Rendered by QuickLaTeX.com” height=”15″ width=”42″ style=”vertical-align: -2px;”> <p class=$ Ad esempio, prendiamo qualsiasi punto maggiore di 5

$x=6:$

$3(6)^2-75$

$108-75$

$+33$

Positivo

Pertanto la funzione senza valore assoluto sarebbe negativa solo nell’intervallo -5<x<5. Dobbiamo quindi esprimere la funzione in parti cambiando solo il segno di questo intervallo:

$\displaystyle f(x)= \lvert 3x^2-75 \rvert = \left\{ \begin{array}{lcl} 3x^2-75 & \text{si} & x<-5 \\[2ex] -(3x^2-75) & \text{si} & -5 \le x \le 5 \\[2ex] 3x^2-75 & \text{si} & x>5 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”97″ width=”408″ style=”vertical-align: 0px;”> 5 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”97″ width=”394″ style=”vertical-align: 0px;”> <div class=$

Esercizio 3

Per rappresentare una funzione con valore assoluto, devi prima rappresentare la funzione senza valore assoluto:

È una funzione affine, quindi è necessario costruire una tabella di valori per rappresentarla graficamente:

Dobbiamo ora disegnare la funzione simmetrica dove la funzione è negativa, cioè dove si trova sotto l’asse X. Pertanto, invertiamo la funzione da x=3 all’indietro:

Esercizio 4

Per rappresentare una funzione con valore assoluto, dobbiamo prima disegnare la funzione senza valore assoluto.

Questa è una funzione quadratica. Quindi per rappresentarla dobbiamo calcolare la coordinata X del vertice della parabola con la sua formula:

Dobbiamo ora tradurre la funzione per simmetria dove è negativa, cioè dove è sotto l’asse OX. Pertanto, invertiamo la funzione da x=0 a x=4: