Funzione tangente iperbolica

In questa pagina troverai tutto sulla tangente iperbolica: qual è la sua formula, la sua rappresentazione grafica, tutte le sue caratteristiche,…

Formula della tangente iperbolica

La funzione tangente iperbolica è una delle principali funzioni iperboliche ed è rappresentata dal simbolo tanh(x) . Matematicamente, la tangente iperbolica è uguale al seno iperbolico diviso per il coseno iperbolico.

$\text{tanh}(x)=\cfrac{\text{senh}(x)}{\text{cosh}(x)}$

Dalla formula del seno iperbolico e dalla formula del coseno iperbolico possiamo arrivare alla seguente espressione:

$\text{tanh}(x)=\cfrac{e^x-e^{-x}}{e^x+e^{-x}}$

Pertanto, la funzione tangente iperbolica è correlata alla funzione esponenziale. Nel seguente link potrete vedere tutte le caratteristiche di queste tipologie di funzioni:

➤ Vedi:caratteristiche delle funzioni esponenziali

Rappresentazione grafica della tangente iperbolica

Dalla sua formula possiamo rappresentare graficamente la funzione tangente iperbolica:

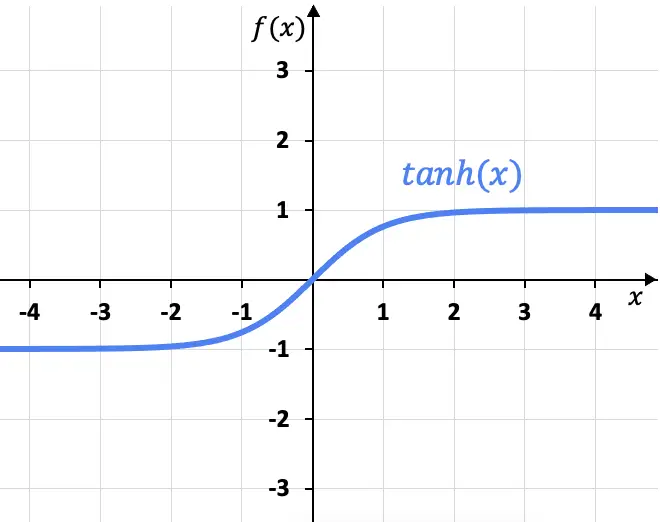
Come puoi vedere dal grafico, la funzione tangente iperbolica ha due asintoti orizzontali in x=+1 e x=-1, poiché il limite della funzione quando x si avvicina a più infinito dà x=+1, e il limite a meno infinito dà x=-1.

D’altro canto il grafico della tangente iperbolica non ha nulla a che vedere con il grafico della tangente (funzione trigonometrica), che è una funzione periodica. Puoi vedere la rappresentazione grafica della tangente e come differisce dalla tangente iperbolica nel seguente link:

➤ Vedi: rappresentazione grafica della funzione tangente

Caratteristiche della tangente iperbolica

La funzione tangente iperbolica ha le seguenti proprietà:

Il dominio della funzione tangente iperbolica è costituito da tutti i numeri reali.

$\text{Dom } f = \mathbb{R}$

Al contrario, il percorso o l’intervallo della funzione tangente iperbolica è limitato a valori compresi tra -1 e +1 (non inclusi).

$\text{Im } f= (-1,1)$

La tangente iperbolica è una funzione continua, biiettiva e dispari (simmetrica rispetto all’origine delle coordinate).

$\displaystyle \text{tanh}(-x) =- \text{tanh}(x)$

La funzione interseca l’asse X e l’asse Y nell’origine delle coordinate.

$(0,0)$

I limiti a più/meno infinito della funzione tangente iperbolica danno +1/-1. Pertanto, la funzione ha un asintoto orizzontale in x=+1 e un altro asintoto orizzontale in x=-1.

$\displaystyle\lim_{x\to+\infty}\text{tanh}(x)=+1$

$\displaystyle\lim_{x\to-\infty}\text{tanh}(x)=-1$

La tangente iperbolica è strettamente crescente su tutto il suo dominio, non ha quindi estremi relativi (né massimo né minimo).

Tuttavia, la funzione cambia da convessa a concava nel punto x = 0, quindi x = 0 è un punto di flesso della funzione.

L’inverso della funzione tangente iperbolica è chiamato argomento tangente iperbolica (o arcotangente iperbolico) e la sua formula è la seguente:

$\displaystyle\text{tanh}^{-1}(x)=\text{arg tanh}(x)=\cfrac{1}{2}\ln\left(\frac{1+x}{1-x}\right)$

La derivata della funzione tangente iperbolica è 1 divisa per il quadrato del coseno iperbolico:

$f(x)=\text{tanh}(x) \ \longrightarrow \ f'(x)=\cfrac{1}{\text{cosh}^2(x)}=1-\text{tanh}^2(x)$

L’integrale della funzione tangente iperbolica è il logaritmo naturale del coseno iperbolico:

$\displaystyle\int\text{tanh}(x) \ dx= \ln\Bigl(\text{cosh}(x)\Bigr)+C$

La tangente iperbolica della somma di due numeri diversi può essere calcolata applicando la seguente equazione:

$\text{tanh}(x+y)=\cfrac{\text{tanh}(x)+\text{tanh}(y)}{1+\text{tanh}(x)\cdot \text{tanh}(y)}$

Il polinomio di Taylor o la serie tangente iperbolica ha il raggio di convergenza
$\left|x\right|<\cfrac{\pi}{2}$

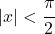
e corrisponde alla seguente espressione:

$\displaystyle\text{tanh}(x)=x-\frac{x^3}{3}+\frac{2x^5}{15}-\frac{17x^7}{315}+\cdots =\sum_{n=1}^\infty\frac{2^{2n}(2^{2n}-1)B_{2n} x^{2n-1}}{(2n)!}$

Oro

$B_n$

è il numero di Bernoulli .

Formula della tangente iperbolica

Rappresentazione grafica della tangente iperbolica

Caratteristiche della tangente iperbolica

Lascia un commento Annulla risposta