Funzione tangente - Mathority

In questa pagina troverai tutto sulla funzione tangente: cos’è, qual è la sua formula, come rappresentarla in un grafico, le caratteristiche della funzione, il suo periodo, ecc. Inoltre, potrai vedere esempi di funzioni tangenti per comprendere appieno il concetto. Spiega anche il teorema della tangente e le relazioni che la funzione tangente ha con altre relazioni trigonometriche.

Formula della funzione tangente

La funzione tangente di un angolo α è una funzione trigonometrica la cui formula è definita come il rapporto tra il ramo opposto e il ramo contiguo (o adiacente) di un triangolo rettangolo (triangolo con un angolo retto).

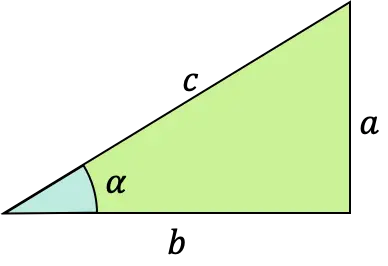
la tangente è una funzione trigonometrica

Questo tipo di funzione matematica è anche chiamata funzione tangente, tangenoide o tangenziale. E può essere espresso con la sigla “tg” o anche “tan”.

La funzione tangente è uno dei tre rapporti trigonometrici più conosciuti, insieme al seno e al coseno di un angolo.

Valori caratteristici della funzione tangente

Ci sono alcuni angoli che si ripetono frequentemente e, quindi, è conveniente conoscere il valore della funzione tangente a questi angoli:

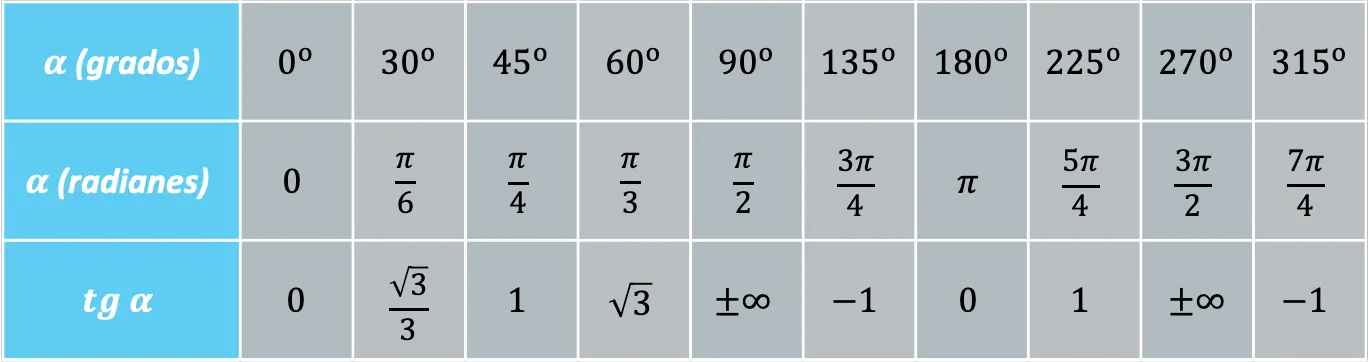
D’altra parte, la funzione tangente può essere collegata alle funzioni seno e coseno dalla seguente identità trigonometrica fondamentale:

$\text{tg } \alpha = \cfrac{\text{sen }\alpha}{\text{cos }\alpha}$

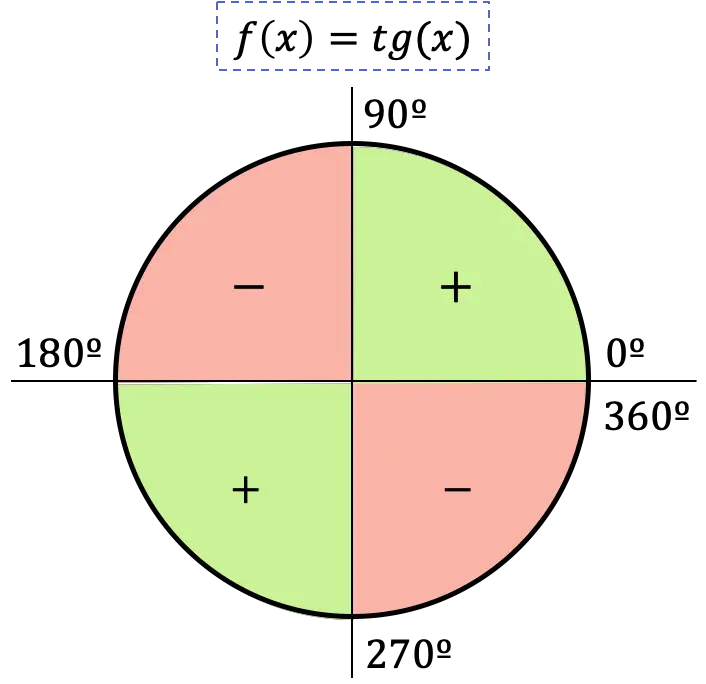
Pertanto, il segno della funzione tangente dipende dal quadrante in cui si trova l’angolo:

Se l’angolo appartiene al primo quadrante, la sua tangente sarà positiva, poiché in questo quadrante sono positivi anche il seno e il coseno.
Se l’angolo cade nel secondo quadrante, la sua tangente sarà negativa, perché in questo quadrante il seno è positivo ma il coseno è negativo.
Se l’angolo si trova nel terzo quadrante, la sua tangente sarà positiva, perché in questo quadrante seno e coseno sono negativi.
Se l’angolo si trova nel quarto quadrante, la sua tangente sarà negativa, poiché in questo quadrante il seno è negativo e invece il coseno è positivo.

Rappresentazione grafica della funzione tangente

Con la tabella dei valori che abbiamo visto nella sezione precedente possiamo rappresentare graficamente la funzione tangente. E rappresentando graficamente la funzione tangente otteniamo:

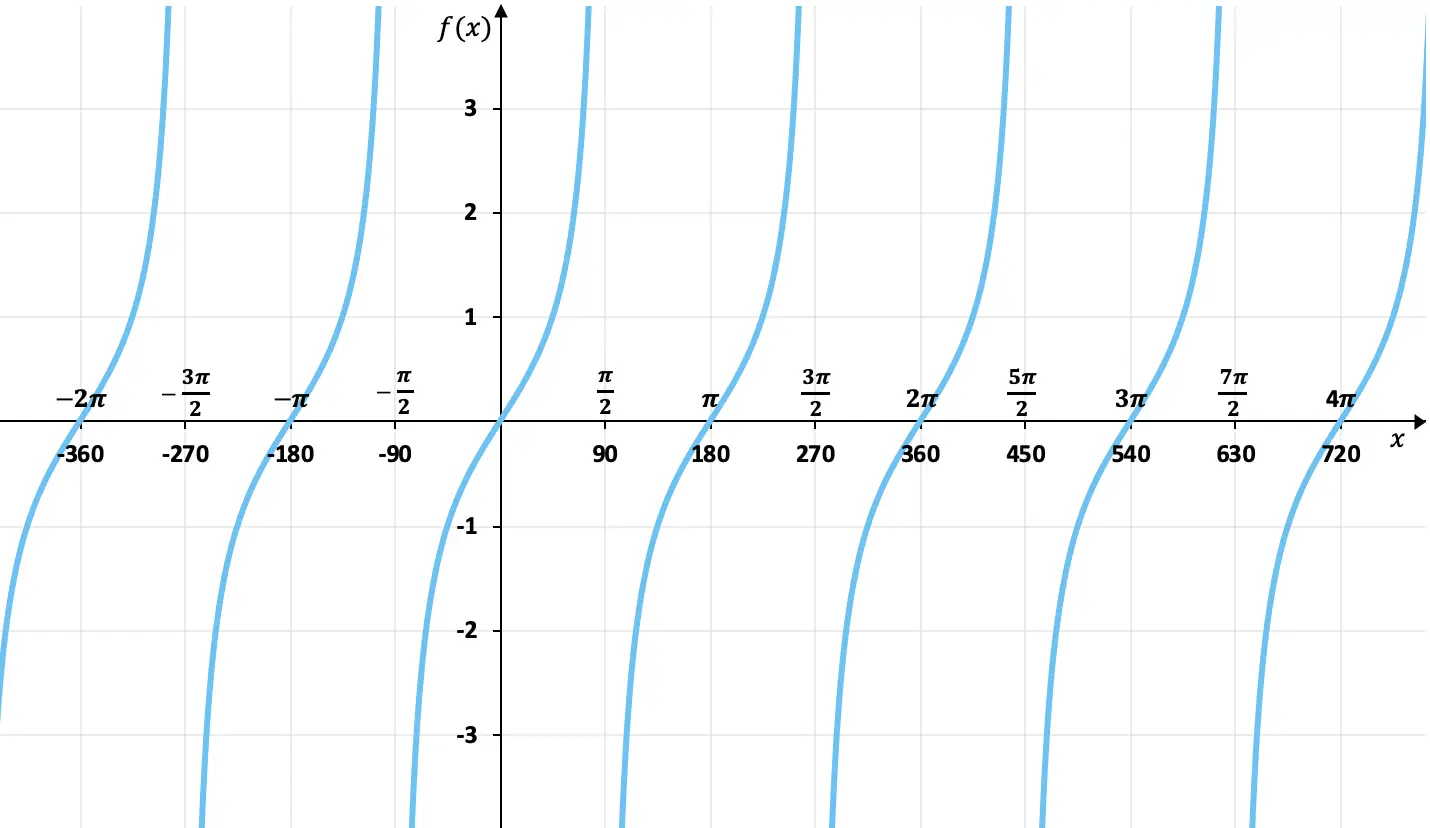
Come puoi vedere dal grafico, i valori delle immagini della funzione tangente non sono limitati, a differenza delle funzioni seno e coseno. Inoltre, i valori si ripetono ogni 180 gradi (π radianti), quindi è una funzione periodica il cui periodo è 180º.

D’altra parte, in questo grafico possiamo vedere che la funzione tangente è dispari , perché i suoi elementi opposti hanno immagini opposte, o in altre parole, è simmetrica rispetto all’origine (0,0). Ad esempio la tangente di 45° vale 1 e quella di -45° vale -1.

Infine, possiamo anche vedere che la funzione tangente ha asintoti verticali . Ad esempio, si avvicina molto alla linea x=90º ma non la tocca mai, e la stessa cosa accade ogni 180 gradi. Ciò significa che il limite della funzione in questi punti tende all’infinito.

Proprietà della funzione tangente

La funzione tangente ha le seguenti caratteristiche:

Il dominio della funzione tangente è costituito da tutti i numeri reali tranne i punti in cui è presente un asintoto verticale:

$\displaystyle \text{Dom } f = \mathbb{R} - \left\{(2k+1)\cdot \frac{\pi}{2} \right\} \qquad k \in \mathbb{Z}$

$\displaystyle \text{Dom } f = \mathbb{R} - \left\{\ldots \ , \ -\frac{\pi}{2} \ , \ \frac{\pi}{2} \ , \ \frac{3\pi}{2} \ , \ \ldots \right\}$

L’intervallo o l’intervallo della funzione tangente sono tutti numeri reali.

$\text{Im } f= \mathbb{R}$

È una funzione continua e dispari con periodicità π.

$\displaystyle \text{tg}(-x) =- \text{tg }x$

Questo tipo di funzione trigonometrica ha un unico punto di intersezione con l’asse y (asse Y) nel punto (0,0).

$(0,0)$

Intercetta invece periodicamente l’ascissa (asse X) in diverse coordinate del pi greco.

$\displaystyle (k\pi ,0) \qquad k \in \mathbb{Z}$

La funzione è strettamente crescente su tutto il dominio, quindi non ha né massimo né minimo.

La derivata della tangente è:

$f(x)=\text{tg } x \ \longrightarrow \ f'(x)= 1+\text{tg}^2 x=\cfrac{1}{\text{cos}^2 x} =\text{sec}^2 x$

Infine, l’integrale della funzione tangente è:

$\displaystyle \int \text{tg } x \ dx= -\ln \lvert \text{cos }x \rvert + C$

Periodo della funzione tangente

A differenza di altre funzioni trigonometriche come seno e coseno, la funzione tangente non ha grandezza poiché non ha né un valore massimo né un valore minimo. Si tratta però di una funzione periodica, cioè i suoi valori si ripetono con la frequenza che abbiamo visto nel grafico.

$\displaystyle f(x)= \text{tg}(wx)$

Il periodo della funzione tangente è la distanza tra due punti in cui si ripete il grafico e si calcola con la seguente formula:

$\displaystyle \text{Periodo}=T=\cfrac{\pi}{w}$

teorema della tangente

Anche se la formula della tangente viene normalmente utilizzata nei triangoli rettangoli, esiste anche un teorema da applicare a qualsiasi tipo di triangolo: il teorema della tangente.

Il teorema della tangente mette in relazione i lati e gli angoli di qualsiasi triangolo come segue:

$\displaystyle \cfrac{a+b}{a-b} = \cfrac{ \text{tg}\left(\frac{\alpha+\beta}{2}\right)}{\text{tg}\left(\frac{\alpha-\beta}{2}\right)}$

$\displaystyle \cfrac{a+c}{a-c} = \cfrac{ \text{tg}\left(\frac{\alpha+\gamma \vphantom{\beta}}{2}\right)}{\text{tg}\left(\frac{\alpha-\gamma\vphantom{\beta}}{2}\right)}$

$\displaystyle \cfrac{b+c}{b-c} = \cfrac{ \text{tg}\left(\frac{\beta+\gamma}{2}\right)}{\text{tg}\left(\frac{\beta-\gamma}{2}\right)}$

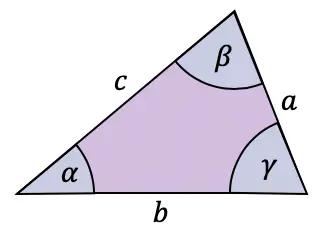
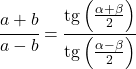
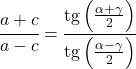
Relazioni della funzione tangente con altri rapporti trigonometrici

Di seguito sono riportate le relazioni della tangente con i rapporti trigonometrici più importanti della trigonometria.

Rapporto con il seno

La tangente e il seno di un angolo sono correlati come segue:

$\displaystyle \text{tg }\alpha = \pm \cfrac{\text{sen }\alpha }{\sqrt{1-\text{sen}^2\alpha \vphantom{\bigl( }}}$

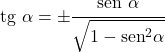
Rapporto coseno

Allo stesso modo, la tangente e il coseno di un angolo sono legati alla seguente uguaglianza:

$\displaystyle \text{tg }\alpha = \pm \cfrac{\sqrt{1-\text{cos}^2\alpha \vphantom{\bigl( }} }{\text{cos }\alpha}$

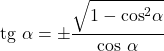
Rapporto con la cosecante

Sebbene sia difficile da dimostrare, la tangente può essere risolta in modo che dipenda solo dalla cosecante:

$\displaystyle \text{tg }\alpha = \pm \cfrac{1}{\sqrt{\text{csc}^2\alpha -1 \vphantom{\bigl( }}}$

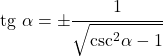
Rapporto con la secante

La tangente e la secante di un angolo sono legate dalla seguente equazione:

$\displaystyle \text{tg }\alpha = \pm\sqrt{\text{sec}^2\alpha -1$

Relazione con la cotangente

Tangente e cotangente sono inversi moltiplicativi:

$\displaystyle \text{tg }\alpha =\pm \cfrac{1}{\text{cot }\alpha}$