Funzione seno iperbolico

In questo articolo troverai tutto sul seno iperbolico: qual è la sua formula, la sua rappresentazione grafica, tutte le sue caratteristiche, le relazioni con le altre funzioni,…

Formula del seno iperbolico

La funzione seno iperbolico è una delle principali funzioni iperboliche ed è rappresentata dal simbolo sinh(x) o sinh(x) . Il seno iperbolico è uguale a e ^x meno e ^-x diviso per 2.

La formula del seno iperbolico è quindi la seguente:

$\displaystyle\text{senh}(x)=\cfrac{e^{x}-e^{-x}}{2}$

Pertanto, il seno iperbolico è correlato alla funzione esponenziale.

➤ Vedi:caratteristiche della funzione esponenziale

Rappresentazione grafica del seno iperbolico

Utilizzando la formula che abbiamo visto nella sezione precedente, possiamo creare una tabella dei valori del seno iperbolico e rappresentare graficamente la funzione:

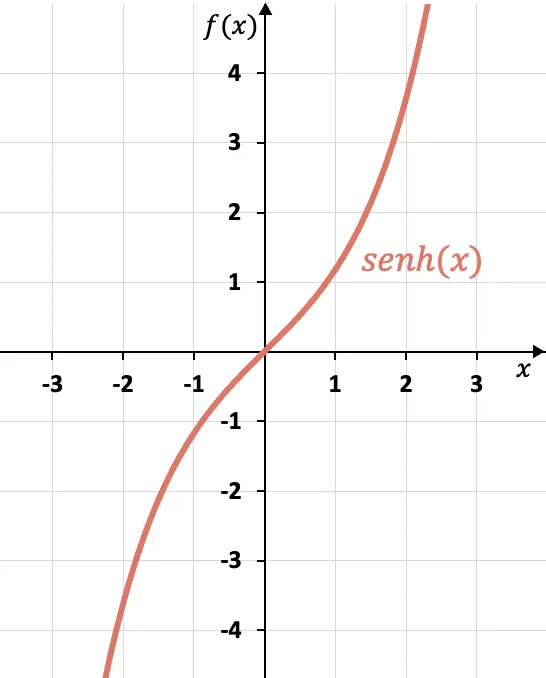
In questo grafico, possiamo vedere che il seno iperbolico è una funzione dispari , perché le x opposte hanno immagini opposte o, in altre parole, il grafico del seno iperbolico è simmetrico rispetto all’origine delle coordinate (0, 0).

Come puoi vedere, il grafico del seno iperbolico è molto diverso da quello del seno, che è una funzione periodica. Puoi vedere la rappresentazione grafica del seno e tutte le differenze con il seno iperbolico nel seguente link:

➤ Vedi: Rappresentazione grafica della funzione seno

Caratteristiche del seno iperbolico

Il seno iperbolico ha le seguenti proprietà:

Il dominio della funzione seno iperbolico è composto da tutti i numeri reali:

$\text{Dom } f = \mathbb{R}$

Anche l’intervallo o l’intervallo della funzione seno iperbolico sono tutti numeri reali.

$\text{Im } f= \mathbb{R}$

Il seno iperbolico è una funzione continua e dispari.

$\displaystyle \text{senh}(-x) =- \text{senh}(x)$

Intercetta l’asse X e l’asse Y nello stesso punto di intersezione, l’origine delle coordinate:

$(0,0)$

Il limite della funzione seno iperbolico quando x tende a più/meno infinito è uguale a più/meno infinito:

$\displaystyle\lim_{x\to+\infty}\text{senh}(x)=+\infty$

$\displaystyle\lim_{x\to-\infty}\text{senh}(x)=-\infty$

Il seno iperbolico è strettamente crescente in tutto il dominio, quindi non ha né massimi né minimi.

Tuttavia, cambia la sua curvatura nel punto x = 0, quindi è un punto di flesso della funzione. Per valori inferiori a x=0 è una funzione concava, invece per valori maggiori di x=0 è una funzione convessa.

La derivata della funzione seno iperbolico è il coseno iperbolico:

$f(x)=\text{senh}(x) \ \longrightarrow \ f'(x)=\text{cosh}(x)$

Allo stesso modo, l’integrale della funzione seno iperbolico è il coseno iperbolico:

$\displaystyle \int \text{senh}(x) \ dx= \text{cosh}(x) + C$

La serie di Taylor della funzione seno iperbolico equivale alla seguente espressione:

$\displaystyle\text{senh}(x)=x+\cfrac{x^3}{3!}+\cfrac{x^5}{5!}+\cfrac{x^7}{7!}+\dots=\sum_{n=0}^\infty\cfrac{x^{2n+1}}{(2n+1)!}$

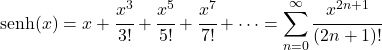
La trasformata di Laplace della funzione seno iperbolico è la seguente:

$\mathcal{L}\bigl[\text{senh}(at)\bigr]=\cfrac{a}{s^2-a^2}$

Relazioni matematiche del seno iperbolico

Il seno iperbolico è collegato alle altre funzioni iperboliche dalle seguenti equazioni:

L’equazione fondamentale mette in relazione il seno iperbolico con il coseno iperbolico:

$\text{cosh}^2(x)-\text{senh}^2(x)=1$

Pertanto, le funzioni seno iperbolico e coseno sono correlate dall’equazione dell’iperbole, che è x ² -y ² =1. A differenza delle funzioni trigonometriche seno e coseno che sono collegate dall’equazione del cerchio (x ² +y ² =1).

Le funzioni iperboliche di seno, coseno e tangente possono essere correlate dalla seguente equazione:

$\text{tanh}(x)=\cfrac{\text{senh}(x)}{\text{cosh}(x)}$

Invece, il seno iperbolico dell’addizione o della sottrazione di due numeri diversi può essere calcolato con le seguenti formule:

$\text{senh}(x+y)=\text{senh}(x)\text{cosh}(y)+\text{senh}(y)\text{cosh}(x)$

$\text{senh}(x-y)=\text{senh}(x)\text{cosh}(y)-\text{senh}(y)\text{cosh}(x)$

Il seno iperbolico del doppio di un numero può essere determinato applicando la seguente relazione matematica:

$\text{senh}(2x)=2\text{senh}(x)\text{cosh}(x)$

La somma o la sottrazione di due seni iperbolici può essere trovata utilizzando le seguenti formule:

$\displaystyle\text{senh}(x)+\text{senh}(y)=2\text{senh}\left(\frac{x+y}{2}\right)\text{cosh}\left(\frac{x-y}{2}\right)$

$\displaystyle\text{senh}(x)-\text{senh}(y)=2\text{senh}\left(\frac{x-y}{2}\right)\text{cosh}\left(\frac{x+y}{2}\right)$

Infine, il quadrato del seno iperbolico può essere calcolato applicando la seguente formula:

$\text{senh}^2(x)=\cfrac{1}{2}\Bigl(\text{cosh}(2x)-1\Bigr)$

Formula del seno iperbolico

Rappresentazione grafica del seno iperbolico

Caratteristiche del seno iperbolico

Relazioni matematiche del seno iperbolico

Lascia un commento Annulla risposta