Funzione razionale: cos'è, dominio, asintoti, grafico, esercizi,...

Qui scoprirai cosa sono le funzioni razionali. Inoltre, spieghiamo come calcolare il dominio e gli asintoti di una funzione razionale. E non solo, ma vedrai quali sono tutte le caratteristiche delle funzioni razionali. Infine, puoi esercitarti con esercizi passo passo sulle funzioni razionali.

Cos’è una funzione razionale?

La definizione di funzione razionale è la seguente:

Una funzione razionale è una funzione formata dal quoziente di due polinomi , cioè una funzione razionale è una frazione che ha un polinomio al numeratore e al denominatore.

Le funzioni razionali sono caratterizzate da singolarità nei punti in cui il denominatore svanisce.

$f(x)=\cfrac{a_0+a_1x+a_2x^2+\dots +a_nx^n}{b_0+b_1x+b_2x^2+\dots +n_nx^n}$

Le funzioni razionali sono anche chiamate funzioni frazionarie.

D’altra parte, le funzioni razionali non vanno confuse con le funzioni irrazionali. Le funzioni irrazionali (o radicali) sono quelle costituite da radici.

Esempi di funzioni razionali

Per comprendere meglio la nozione di funzione razionale, vedremo diversi esempi di questo tipo di funzione.

Funzione razionale con un polinomio di primo grado al numeratore e al denominatore:

$f(x)=\cfrac{x+3}{2x-5}$

Questi tipi di funzioni razionali sono anche chiamate funzioni omografe .

Funzione razionale con una costante al numeratore e un polinomio al denominatore:

$f(x)=\cfrac{7}{x+1}$

Questi tipi di funzioni razionali sono chiamate funzioni di proporzionalità inversa e vengono utilizzate per definire matematicamente quantità inversamente proporzionali.

Funzione razionale con un polinomio di terzo grado al numeratore e un polinomio di secondo grado al denominatore:

$f(x)=\cfrac{x^3+4x^2-2x+6}{x^2+3x-1}$

Dominio di una funzione razionale

Un numero diviso per 0 è un’indeterminazione che dà infinito (∞), quindi esisterà sempre una funzione razionale a meno che il denominatore non sia 0.

Pertanto il dominio di una funzione razionale è costituito da tutti i numeri reali tranne i valori che annullano il denominatore.

Quindi, per ottenere il dominio di una funzione razionale, dobbiamo trovare quando il denominatore è 0, poiché questo punto sarà l’unico a non appartenere al dominio

Vediamo come si calcola il dominio di una funzione razionale risolvendo un esempio:

$f(x)=\cfrac{5x}{x+2}$

Per prima cosa impostiamo il denominatore uguale a 0, quindi risolviamo l’equazione risultante:

$x+2=0$

$x=-2$

Pertanto, quando x è -2, il denominatore sarà 0 e quindi la funzione non esisterà. Il dominio della funzione è quindi costituito da tutti i numeri reali tranne x=-2. Ciò è affermato come segue:

$\text{Dom } f= \mathbb{R}-\{ -2 \}$

Asintoti di una funzione razionale

Una delle principali proprietà delle funzioni razionali sono i loro asintoti, poiché ne determinano la rappresentazione grafica.

➤ Vedi: rappresentazione grafica di una funzione

Gli asintoti di una funzione razionale sono linee a cui il grafico della funzione si avvicina indefinitamente ma non tocca mai.

Esistono tre tipi di asintoti: asintoti verticali, asintoti orizzontali e asintoti obliqui.

Di seguito sono riportati i tre tipi di asintoti che una funzione razionale può avere graficamente in rosso.

Asintoto verticale di una funzione razionale

Asintoto orizzontale di una funzione razionale

Asintoto obliquo di una funzione razionale

Come puoi vedere, determinare l’asintoto di una funzione dal suo grafico è abbastanza semplice, ma calcolare gli asintoti di una funzione razionale senza avere la sua rappresentazione grafica è piuttosto complicato. Per questo motivo ti consigliamo di vedere come vengono calcolati gli asintoti di una funzione sul nostro sito web.

Caratteristiche di una funzione razionale

Le funzioni razionali hanno le seguenti caratteristiche:

$f(x)=\cfrac{P(x)}{Q(x)}$

Come abbiamo visto sopra, il dominio delle funzioni razionali comprende tutti i numeri reali tranne i valori che annullano il denominatore della frazione.

In generale, l’intervallo (o intervallo) di una funzione razionale comprende tutti i numeri reali tranne i valori in cui la funzione ha un asintoto orizzontale.

Le funzioni razionali sono continue in tutto il loro dominio. O in altre parole, le funzioni razionali presentano discontinuità in punti che non appartengono al loro dominio.

La rappresentazione grafica della maggior parte delle funzioni razionali è costituita da due iperboli.

Alcune regole per gli asintoti delle funzioni razionali possono essere dedotte dal numeratore del polinomio.
$P(x)$

e il polinomio del denominatore

$Q(x):$
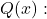
- Una funzione razionale ha un asintoto verticale nei punti che ne sono le radici
  $Q(x)$
  
  ma queste non sono radici di
  
  $P(x).$
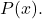
- Se il grado di
  $P(x)$
  
  è inferiore al grado di
  
  $Q(x)$
  
  , la retta y=0 è un asintoto orizzontale della funzione razionale.
- Se il grado di
  $P(x)$
  
  è maggiore del grado di
  
  $Q(x)$
  
  , la funzione razionale non ha asintoto orizzontale.
- Se il grado di
  $P(x)$
  
  è un’unità maggiore del grado di
  
  $Q(x)$
  
  e i due polinomi non hanno radice comune, la funzione razionale ha un asintoto obliquo.

Esercizi risolti su funzioni razionali

Esercizio 1

Trovare il dominio della seguente funzione razionale:

$f(x)=\displaystyle\frac{4x}{2x+4}$

Vedi la soluzione

È una funzione razionale, quindi il dominio è formato da tutti i numeri tranne quelli che annullano il denominatore, perché in tal caso la funzione darebbe ∞.

Quindi impostiamo il denominatore intero uguale a zero per vedere quale numero non appartiene al dominio:

$2x+4=0$

E risolviamo l’equazione risultante:

$2x=-4$

$x=\cfrac{-4}{2}=-2$

Il dominio della funzione è quindi composto solo da numeri tranne -2:

$\mathbf{Dom } \ \bm{f = \mathbb{R}- \{ -2 \} }$

Esercizio 2

Trova i punti di interruzione della seguente funzione razionale con gli assi cartesiani:

$f(x)=\cfrac{x^2-9}{x}$

Vedi la soluzione

Punto di taglio con asse X

Per trovare il punto di intersezione della funzione con l’asse X è necessario risolvere

$f(x)=0:$

$f(x)=0$

$\cfrac{x^2-9}{x}=0$

$x^2-9=0\cdot x$

$x^2-9=0$

$x^2=9$

$x^2=\pm 3$

Abbiamo ottenuto due soluzioni dell’equazione quadratica, quindi la funzione razionale interseca l’asse delle ascisse in due punti diversi, che sono:

$\bm{(3,0)\qquad (-3,0)}$

Punto di taglio con asse Y

Per trovare il punto di intersezione con l’asse Y devi calcolare

$f(0):$

$f(0)=\cfrac{0^2-9}{0}=\cfrac{-9}{0}= \infty$

Qualsiasi numero diviso per zero è un’indeterminazione che dà infinito. Pertanto la funzione razionale non passa in nessun punto al di sopra dell’asse Y, cioè non ha punti di intersezione con l’asse y.

Esercizio 3

Traccia su un grafico la seguente funzione razionale:

$y=\cfrac{2x+3}{2x+6}$

Vedi la soluzione

La prima cosa da fare è calcolare il dominio della funzione:

$2x+6=0$

$2x =-6$

$x =\cfrac{-6}{2} =-3$

$\text{Dom } f = \mathbb{R} - \{ -3 \}$

Una volta conosciuto il dominio della funzione, costruiamo una tabella di valori:

$\begin{array}{c|c} x & y \\ \hline -2,5 & -2 \\ -2 & -0,5 \\ -1 & 0,25 \\ 1 & 0,63 \\ -3,5 & 4 \\ -4 & 2,5 \\ -5 & 1,75 \\ -7 & 1,38\end{array}$

Per finire basta rappresentare su un grafico i punti ottenuti e tracciare le iperboli, disegnando così la funzione razionale:

Esercizio 4

Determina gli asintoti della funzione razionale rappresentata nel grafico seguente:

Vedi la soluzione

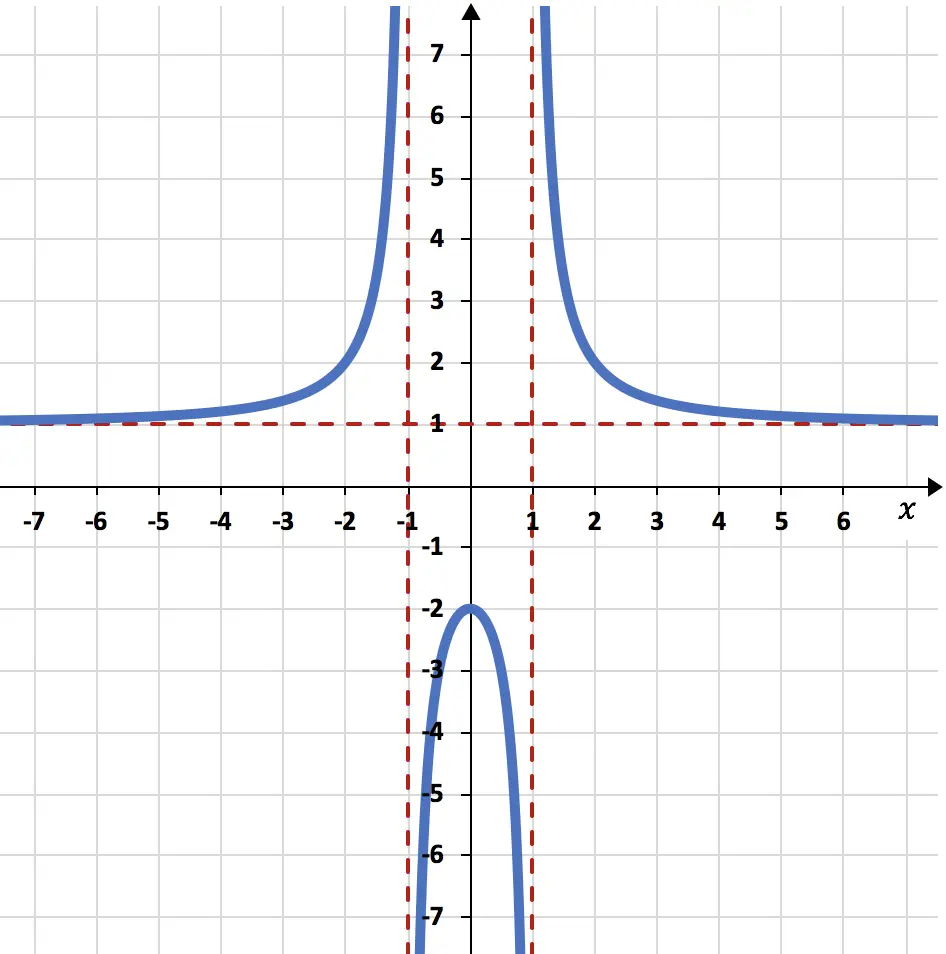
Gli asintoti sono molto chiaramente visibili sul grafico, poiché sono rappresentati come linee tratteggiate rosse.

In questo problema la funzione è molto vicina alla linea orizzontale y=1 ma non la tocca mai. Pertanto, la funzione razionale ha un unico asintoto orizzontale, che è y=1.

Allo stesso modo, la rappresentazione grafica della funzione è molto vicina alle linee verticali x=-1 e x=1, ma non raggiunge mai questi valori. La funzione razionale ha quindi due diversi asintoti verticali, che sono x=-1 e x=1.

Esercizio 5

Calcola tutti gli asintoti della seguente funzione razionale:

$\displaystyle f(x)=\frac{6x-4}{2x+2}$

Nota: per risolvere questo esercizio, ti consigliamo di andare prima al link sopra su come vengono calcolati gli asintoti di una funzione e vedere la spiegazione.

Vedi la soluzione

asintoto verticale

Per calcolare gli asintoti verticali di una funzione, dobbiamo prima trovare il dominio della funzione. Pertanto, poniamo il denominatore della funzione razionale uguale a 0 per trovare i punti che non appartengono al dominio:

$2x +2 =0$

$2x= -2$

$x = \cfrac{-2}{2} = -1$

Il dominio della funzione è quindi costituito da tutti i numeri tranne -1:

$\text{Dom } f = \mathbb{R} - \left\{ -1 \right\}$

Quindi x=-1 potrebbe essere un asintoto verticale. Per verificarlo dobbiamo calcolare il limite della funzione nel punto:

$\displaystyle \lim_{x \to -1 } \frac{6x-4}{2x+2} = \frac{6\cdot(-1)-4}{2\cdot(-1)+2}=\frac{-10}{0}= \infty$

Pertanto x=-1 è un asintoto verticale della funzione razionale, poiché il limite della funzione in questo punto dà infinito.

asintoto orizzontale

Per determinare gli asintoti orizzontali, dobbiamo calcolare il limite infinito della funzione:

$\displaystyle \lim_{x \to +\infty}\frac{6x-4}{2x+2} = \frac{6(+\infty)}{2(+\infty)} = \frac{+\infty}{+\infty} = \frac{6}{2} = \bm{3}$

$\displaystyle \lim_{x \to -\infty}\frac{6x-4}{2x+2} = \frac{6(-\infty)}{2(-\infty)} = \frac{-\infty}{-\infty} = \frac{6}{2} = \bm{3}$

In questo caso, il risultato del limite infinito indeterminato tra infinito è la divisione dei coefficienti delle x di grado massimo, poiché il numeratore e il denominatore sono dello stesso ordine.

I due limiti infiniti della funzione ci hanno dato 3, quindi y=3 è un asintoto orizzontale della funzione razionale.

asintoto obliquo

Poiché esiste un asintoto orizzontale, la funzione razionale non ha un asintoto obliquo.

Cos’è una funzione razionale?

Esempi di funzioni razionali

Dominio di una funzione razionale

Asintoti di una funzione razionale

Caratteristiche di una funzione razionale

Esercizi risolti su funzioni razionali

Esercizio 1

Esercizio 2

Esercizio 3

Esercizio 4

Esercizio 5

Lascia un commento Annulla risposta