Funzione polinomiale

Qui troverai cosa sono le funzioni polinomiali e quali sono tutti i tipi di funzioni polinomiali. Inoltre, spieghiamo anche le proprietà delle funzioni polinomiali.

Cos’è una funzione polinomiale?

Una funzione polinomiale è una funzione la cui espressione algebrica è un polinomio , cioè una funzione polinomiale è definita dall’addizione o sottrazione di un numero finito di termini di diverso grado.

Pertanto, una funzione polinomiale è descritta matematicamente dalla seguente espressione:

$f(x)=a_0+a_1x+a_2x^2+a_3x^3+\dots+a_nx^n$

D’altra parte, le funzioni polinomiali possono anche essere definite utilizzando la seguente formula:

$\displaystyle f(x)=\sum_{k=0}^{n}a_k\cdot x^k$

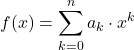
dove i termini

$a_k$

$x^k$

sono rispettivamente il coefficiente e la variabile di ciascun monomio che forma la funzione polinomiale.

Il termine

$a_nx^n$

, detto termine principale, indica il grado della funzione polinomiale, poiché è il monomio di grado più alto della funzione. In altre parole, l’esponente del valore più grande è quello che indica il grado della funzione polinomiale.

Anche se di seguito vedremo più caratteristiche delle funzioni polinomiali, il dominio di qualsiasi funzione polinomiale è costituito da tutti i numeri reali.

Tipi di funzioni polinomiali

Data la definizione di funzione polinomiale, vedremo ora quali esistono tutti i tipi di funzioni polinomiali.

funzione costante

La funzione costante è una funzione polinomiale di grado 0, quindi è un tipo di funzione che assume sempre la stessa immagine per qualsiasi valore della variabile indipendente (x).

L’espressione generale per la funzione costante è la seguente:

$f(x)=k$

Ad esempio, le seguenti tre funzioni sono costanti o funzioni polinomiali di grado zero:

$f(x)=5 \qquad f(x)=2 \qquad f(x)=-3$

La rappresentazione grafica di una funzione costante è una linea orizzontale (parallela all’asse x) con un valore uguale alla costante.

Puoi vedere più funzionalità su questo tipo di funzione nel seguente link:

➤ Vedi: caratteristiche della funzione costante

Funzione lineare

Una funzione lineare , detta anche funzione affine, è una funzione polinomiale di primo grado. Quindi una funzione polinomiale di questo tipo può essere composta solo da un termine lineare e da un termine indipendente:

$f(x)=mx+n$

Oro

$m$

è la pendenza della retta e

$n$

è l’intercetta y, cioè il punto in cui la funzione incrocia l’asse Y.

Esempi di funzioni lineari o funzioni polinomiali di primo grado:

$f(x)=4x+3\qquad f(x)=-5x$

Alcuni distinguono la funzione lineare dalla funzione affine a seconda che la funzione abbia come termine

$n$

oppure no, essendo la funzione affine con l’intercetta e la funzione lineare senza.

La rappresentazione grafica delle funzioni lineari sono sempre linee il cui grado di inclinazione dipende dal valore della pendenza della funzione.

Qui sotto puoi vedere graficamente la funzione polinomiale di primo grado

$f(x)=2x-1.$

Tuttavia, per rappresentare graficamente una funzione lineare, è necessario avere chiari alcuni concetti. Nel seguente link troverai la spiegazione passo passo di come rappresentare graficamente una funzione polinomiale di questo tipo:

➤ Vedi: Rappresentazione grafica di una funzione lineare

Funzione quadratica

Una funzione quadratica è una funzione polinomiale di grado 2, cioè una funzione il cui termine di grado superiore è di secondo grado.

Pertanto, la formula per una funzione quadratica è:

$f(x)=ax^2+bx+c$

Oro

$ax^2$

è il termine quadratico,

$bx$

il termine lineare e

$c$

il termine indipendente della funzione polinomiale.

Esempi di funzioni quadratiche o funzioni polinomiali quadratiche:

$f(x)=5x^2+2x-1\qquad f(x)=-2x^2+x+7$

Il grafico di una funzione quadratica è sempre una parabola e la sua forma dipende dal segno del coefficiente principale.

$a:$

Se il coefficiente
$a$

è positivo, la funzione quadratica è convessa (a forma di

$\bm{\cup}$

).
Se invece il coefficiente
$a$

è negativo, la funzione quadratica è concava (a forma di

$\bm{\cap}$

).

Quindi, con il segno del coefficiente principale della funzione polinomiale quadratica, possiamo conoscere la forma che assumerà il suo grafico, ma per realizzarne l’esatta rappresentazione grafica occorre seguire una procedura specifica. Puoi vedere questa procedura nel seguente link:

➤ Vedi: Rappresentazione grafica di una funzione quadratica

funzione cubica

Una funzione cubica è una funzione polinomiale di terzo grado. Pertanto, questo tipo di funzioni polinomiali si esprime algebricamente come segue:

$f(x)=ax^3+bx^2+cx+d$

Esempi di funzioni cubiche o funzioni polinomiali di terzo grado:

$f(x)=x^3+4x^2+5x-1$

$f(x)=2x^3-3x^2+9$

Le rappresentazioni grafiche delle funzioni cubiche corrispondono alle curve cubiche. Tuttavia, per rappresentare questo tipo di funzioni in un grafico è necessario seguire una procedura complicata (che include le derivate). Puoi vedere come è fatto qui:

➤ Vedi: Come rappresentare una funzione

Come puoi vedere, i tipi di funzioni polinomiali sono in realtà infiniti, poiché un polinomio può avere infiniti termini. Quindi, ad esempio, una funzione quartica è come una funzione cubica ma con l’aggiunta di un termine quadratico. L’importante è che tu capisca che il tipo di funzione polinomiale è contrassegnato dal grado della funzione.

Proprietà delle funzioni polinomiali

Le funzioni polinomiali hanno le seguenti caratteristiche:

Il dominio di qualsiasi funzione polinomiale è l’insieme dei numeri reali.

$\text{Dom } f=\mathbbf{R}$

Tutte le funzioni polinomiali sono continue.

Le funzioni polinomiali di grado maggiore di 1 non hanno asintoti.

Qualunque sia il tipo di funzione polinomiale, l’unico punto di intersezione con l’asse delle ordinate (asse Y) è all’altezza del suo termine indipendente, cioè nel punto seguente:

$(0,a_0)$

Una funzione polinomiale, invece, intercetta l’asse delle ascisse (asse X), al massimo tante volte quanto è il grado della funzione.

Se una funzione polinomiale ha solo termini di grado pari, ciò implica che è simmetrica rispetto all’asse OY. D’altra parte, se una funzione polinomiale ha solo termini di grado dispari, ciò significa che la funzione è simmetrica rispetto all’origine delle coordinate.

Il numero di estremi relativi (massimo o minimo) di una funzione polinomiale è, al massimo, il grado del polinomio della funzione meno 1.

Il numero di punti di flesso di una funzione polinomiale è al massimo uguale al grado del polinomio della funzione meno 2.

Le operazioni possono essere eseguite con funzioni polinomiali:
- La somma di due funzioni polinomiali dà un’altra funzione polinomiale.
- Il prodotto di due funzioni polinomiali dà origine ad un’altra funzione polinomiale.
- Moltiplicando una funzione polinomiale per uno scalare (numero reale) si ottiene una funzione polinomiale simile ma con il grafico ridotto o espanso.
- La composizione di due funzioni polinomiali è uguale a un’altra funzione polinomiale.