▷ Cos'è e come rappresentare una funzione quadratica (o parabola)

Questa pagina spiega cos’è una funzione quadratica e tutte le sue caratteristiche: curvatura, vertice, punti di intersezione con gli assi, ecc. Imparerai anche come rappresentare una funzione quadratica su un grafico. E infine, puoi esercitarti con esempi, esercizi passo passo e problemi sulle funzioni quadratiche.

Cos’è una funzione quadratica?

La definizione di funzione quadratica è la seguente:

In matematica, una funzione quadratica (o parabolica) è una funzione polinomiale di grado 2, cioè una funzione in cui il termine di grado più alto è di secondo grado. Pertanto, la formula per una funzione quadratica è:

$f(x)=ax^2+bx+c$

Oro:

$ax^2$

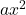
è il termine quadratico.
$bx$

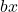
è il termine lineare.
$c$

è il termine indipendente.

Il dominio di una funzione quadratica è sempre costituito da numeri reali.

$\text{Dom } f=\mathbff{R}$

Concavità e convessità di una funzione quadratica

Analizzare la curvatura di una funzione quadratica o parabolica è molto semplice, perché dipende solo dal coefficiente quadratico.

Se il coefficiente
$a$

è positivo, la funzione quadratica è convessa (nella forma

$\bm{\cup}$

). Il vertice è quindi un minimo.
Se il coefficiente
$a$

è negativo, la funzione quadratica è concava (a forma di

$\bm{\cap}$

). Il picco è quindi un massimo.

Nota: La comunità matematica non è ancora del tutto d’accordo e, quindi, alcuni professori dicono il contrario: chiamano concava una funzione che ha la forma di un

$\bm{\cup}$

, e una funzione convessa che ha la forma di

$\bm{\cap}$

. In ogni caso, l’importante è quale forma abbia la funzione, qualunque sia il nome.

Vertice di una funzione quadratica

Per rappresentare graficamente una funzione quadratica è necessario conoscere le coordinate del vertice della parabola.

Per trovare il vertice di una funzione quadratica, dobbiamo calcolare la coordinata X del punto utilizzando la seguente formula:

$\displaystyle x=\frac{-b}{2a}$

Quindi possiamo trovare l’altra coordinata del vertice calcolando l’immagine della funzione in quel punto:

$\displaystyle f\left(\frac{-b}{2a}\right)$

Pertanto le coordinate del vertice di una funzione quadratica (o parabola) sono:

$\displaystyle \left(\frac{-b}{2a} \ , \ f\left(\frac{-b}{2a}\right)\right)$

Punti di taglio con gli assi di una funzione quadratica

Una parabola interseca sempre l’asse y (asse Y), e questo accade quando

$x=0.$

Pertanto, per calcolare il punto limite di una funzione quadratica con l’asse Y, è necessario risolvere

$f(0).$

Ad esempio, il punto di intersezione con l’asse OY della seguente funzione quadratica è:

$f(x)=x^2-2x+1$

$f(0)=0^2-2\cdot 0+1 = 1$

$\bm{(0,1)}$

D’altra parte, il punto limite di una funzione quadratica con l’asse x (asse X) si verifica quando

$f(x)=0.$

Quindi per calcolare il punto di intersezione con l’asse X devi risolvere l’equazione

$f(x)=0.$

Ad esempio, di seguito è riportato il calcolo del punto di interruzione con l’asse OX della stessa funzione quadratica:

$f(x)=x^2-2x+1$

$0=x^2-2x+1$

Risolviamo l’equazione quadratica con la formula generale:

$x=\cfrac{-b\pm \sqrt{b^2-4ac}}{2a}$

$x=\cfrac{-(-2)\pm \sqrt{(-2)^2-4\cdot 1\cdot1}}{2\cdot 1} =\cfrac{2\pm 0}{2} = 1$

Il punto di intersezione della funzione quadratica con l’asse X è quindi:

$\bm{(1,0)}$

In questo caso, abbiamo ottenuto una sola soluzione dell’equazione quadratica, ma avremmo potuto ottenere due soluzioni. In questo caso ciò significa che la funzione quadratica interseca l’asse X in due punti diversi.

Esempio di rappresentazione di una funzione quadratica o parabolica

Vediamo come rappresentare una funzione quadratica su un grafico utilizzando un esempio.

Rappresentare graficamente la seguente funzione:

$f(x)=x^2-4x+5$

La prima cosa da fare è calcolare il vertice della parabola. Per fare ciò utilizziamo la formula che abbiamo visto sopra:

$x = \cfrac{-b}{2a} = \cfrac{-(-4)}{2\cdot 1}= \cfrac{4}{2}= 2$

Una volta che sappiamo dove sarà il vertice, dobbiamo costruire una tabella di valori: Calcoliamo il valore della funzione al vertice e nei punti che lo circondano:

$f(x)=x^2-4x+5$

$x= 2 \ \longrightarrow \ f(2) = 2^2-4\cdot2+5=1$

$x= 1 \ \longrightarrow \ f(1)=1^2-4\cdot1+5=2$

$x= 3 \ \longrightarrow \ f(3) = 3^2-4\cdot3+5=2$

$x= 0 \ \longrightarrow \ f(0) = 0^2-4\cdot0+5=5$

$x= 4 \ \longrightarrow \ f(4) = 4^2-4\cdot4+5=5$

$\begin{array}{c|c} x & f(x) \\ \hline 2 & 1 \\ 1 & 2 \\ 3 & 2 \\ 0 & 5 \\ 4 & 5 \end{array}$

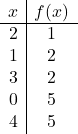
Puoi anche calcolare i punti di taglio della funzione quadratica con gli assi cartesiani per disegnare meglio la parabola, ma questo non è strettamente necessario.

Rappresentiamo ora i punti ottenuti su un grafico :

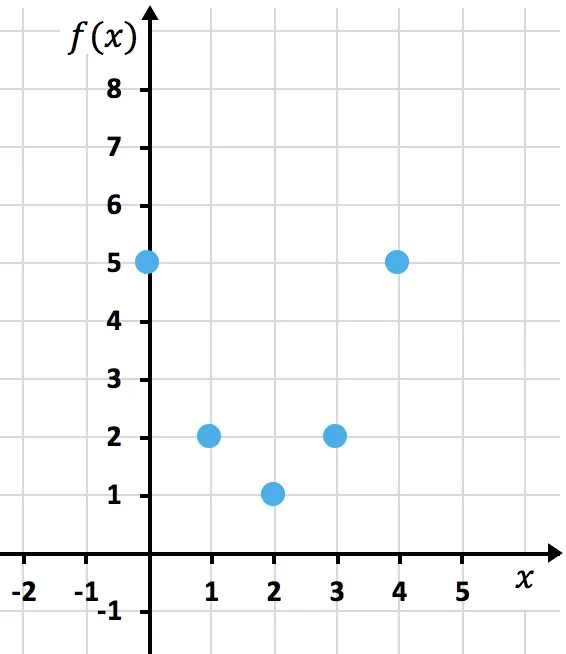
esempio di come rappresentare una funzione quadratica o parabolica

E infine uniamo i punti che formano la parabola. Allora allunghiamo i rami della parabola per indicare che continua verso l’alto:

rappresentazione di una funzione quadratica o parabolica

Esercizi risolti sulle funzioni quadratiche

Esercizio 1

Trova il vertice della seguente funzione quadratica:

$f(x)=2x^2+8x+4$

Vedi la soluzione

Per prima cosa calcoliamo la coordinata X del vertice utilizzando la formula:

$x = \cfrac{-b}{2a} = \cfrac{-8}{2\cdot 2} = \cfrac{-8}{4} = -2$

E ora calcoliamo l’altra coordinata valutando la funzione nel punto:

$\begin{aligned} f(-2) & =2(-2)^2+8(-2)+4 \\[1.7ex] & = 2 \cdot 4 - 16 +4 \\[1.7ex] & = 8-16+4 \\[1.7ex] & = -4 \end{aligned}$

Il vertice della funzione quadratica è quindi:

$\bm{(-2,-4)}$

Esercizio 2

Trova i punti limite della seguente funzione con gli assi:

$f(x)=x^2-4x+3$

Vedi la soluzione

Per calcolare il punto di taglio con l’asse Y, dobbiamo calcolare

$f(0):$

$f(0)=0^2-4\cdot 0+3 = 3$

La funzione passa quindi per l’asse Y nel punto:

$\bm{(0,3)}$

E per trovare i punti di taglio con l’asse X dobbiamo risolvere

$f(x)=0:$

$f(x)=x^2-4x+3$

$0=x^2-4x+3$

Calcoliamo le radici dell’equazione quadratica con la formula:

$x=\cfrac{-b\pm \sqrt{b^2-4ac}}{2a}$

$\displaystyle x=\cfrac{-(-4)\pm \sqrt{(-4)^2-4\cdot 1\cdot 3}}{2\cdot 1} =\cfrac{4\pm 2}{2} = \begin{cases} 3 \\[2ex] 1 \end{cases}$

La funzione taglia quindi l’asse X in due punti:

$\bm{(1,0) \qquad (3,0)}$

Esercizio 3

Rappresentare graficamente la seguente funzione quadratica:

$f(x)=-x^2+4x+1$

Vedi la soluzione

Questa è una funzione quadratica. di conseguenza, per rappresentarlo bisogna prima calcolare l’ascissa del vertice della parabola con la formula:

$x = \cfrac{-b}{2a} = \cfrac{-4}{2\cdot (-1)} = \cfrac{-4}{-2} = 2$

Ora creiamo la tabella dei valori. Per fare ciò, calcoliamo il valore di

$f(x)$

in alto e intorno alla parte superiore:

$x= 2 \ \longrightarrow \ f(2)=-2^2+4\cdot2+1 = 5$

$x= 1 \ \longrightarrow \ f(1)=-1^2+4\cdot1+1 = 4$

$x= 3 \ \longrightarrow \ f(3)=-3^2+4\cdot3+1 =4$

$x= 0 \ \longrightarrow \ f(0)=-0^2+4\cdot0+1 = 1$

$x= 4 \ \longrightarrow \ f(4)=-4^2+4\cdot4+1 = 1$

$\begin{array}{c|c} x & f(x) \\ \hline 2 & 5 \\ 1 & 4 \\ 3 & 4 \\ 0 & 1 \\ 4 & 1 \end{array}$

Infine tracciamo i punti sul grafico e disegniamo la parabola:

Esercizio 4

Rappresentare graficamente la seguente funzione quadratica:

$f(x)=-2x^2-8x-1$

Vedi la soluzione

Questa è una funzione del secondo ordine. di conseguenza per rappresentarlo bisogna prima trovare l’ascissa del vertice della parabola con la formula:

$x = \cfrac{-b}{2a} = \cfrac{-(-8)}{2\cdot (-2)} = \cfrac{+8}{-4} = -2$

Ora costruiamo la tabella dei valori. Per fare ciò, calcoliamo il valore di

$f(x)$

in alto e intorno alla parte superiore:

$x= -2 \ \longrightarrow \ f(-2)=-2(-2)^2-8\cdot(-2)-1 =7$

$x= -1 \ \longrightarrow \ f(-1)=-2(-1)^2-8\cdot(-1)-1= 5$

$x= -3 \ \longrightarrow \ f(-3)=-2(-3)^2-8\cdot(-3)-1= 5$

$x= 0 \ \longrightarrow \ f(0)=-2\cdot0^2-8\cdot0-1= -1$

$x= -4 \ \longrightarrow \ f(-4)=-2(-4)^2-8\cdot(-4)-1= -1$

$\begin{array}{c|c} x & f(x) \\ \hline -2 & 7 \\ -1 & 5 \\ -3 & 5 \\ 0 & -1 \\ -4 & -1 \end{array}$

Infine tracciamo i punti sul grafico e disegniamo la parabola:

esercizio risolto passo dopo passo della funzione quadratica

Esercizio 5

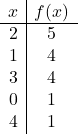
Traccia la seguente funzione quadratica incompleta su un grafico:

$f(x)=x^2+2$

Vedi la soluzione

È una funzione polinomiale di grado due. di conseguenza, per rappresentarlo bisogna prima calcolare l’ascissa del vertice della parabola con la formula:

$x = \cfrac{-b}{2a} = \cfrac{-0}{2\cdot1} = \cfrac{0}{2} = 0$

In questo caso la funzione è incompleta, poiché non ha un termine di primo grado. Per quello

$b=0 .$

Ora creiamo la tabella dei valori. Per fare ciò, calcoliamo il valore di

$f(x)$

in alto e intorno alla parte superiore:

$x= 0 \ \longrightarrow \ f(0)=0^2+2=2$

$x= 1 \ \longrightarrow \ f(1)=1^2+2=3$

$x= -1 \ \longrightarrow \ f(-1)=(-1)^2+2=3$

$x= 2 \ \longrightarrow \ f(2)=2^2+2=6$

$x= -2 \ \longrightarrow \ f(-2)=(-2)^2+2=6$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 2 \\ 1 & 3 \\ -1 & 3 \\ 2 & 6 \\ -2 & 6 \end{array}$

Infine tracciamo i punti sul grafico e disegniamo la parabola:

esercizi risolti per rappresentare una funzione quadratica incompleta

Esercizio 6

Risolvi il seguente problema relativo alle funzioni quadratiche:

Il costo di produzione di un prodotto è definito dalla seguente funzione:

$f(x)=x^2-12x+76$

Oro

$x$

sono le unità prodotte (in migliaia) e

$f(x)$

è il costo di produzione delle unità (in migliaia di euro).

Rappresenta la funzione del costo di produzione su un grafico.
Determinare quante migliaia di unità dovrebbero essere prodotte per ridurre al minimo i costi.

Vedi la soluzione

Questa è una funzione quadratica. di conseguenza per rappresentarlo bisogna prima trovare l’ascissa del vertice della parabola con la formula:

$x = \cfrac{-b}{2a} = \cfrac{-(-12)}{2\cdot 1} = \cfrac{12}{2} = 6$

Ora creiamo la tabella dei valori. Per fare ciò, calcoliamo il valore di

$f(x)$

in alto e intorno alla parte superiore:

$x= 6 \ \longrightarrow \ f(6)=6^2-12\cdot6+76 = 40$

$x= 5 \ \longrightarrow \ f(5)=5^2-12\cdot5+76 = 41$

$x= 7 \ \longrightarrow \ f(7)=7^2-12\cdot7+76 = 41$

$x= 4 \ \longrightarrow \ f(4)=4^2-12\cdot4+76 = 44$

$x= 8 \ \longrightarrow \ f(8)=8^2-12\cdot8+76 = 44$

$\begin{array}{c|c} x & f(x) \\ \hline 6 & 40 \\ 5 & 41 \\ 7 & 41 \\ 4 & 44 \\ 8 & 44 \end{array}$

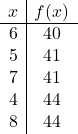
Ora tracciamo i punti sul grafico e disegniamo la parabola:

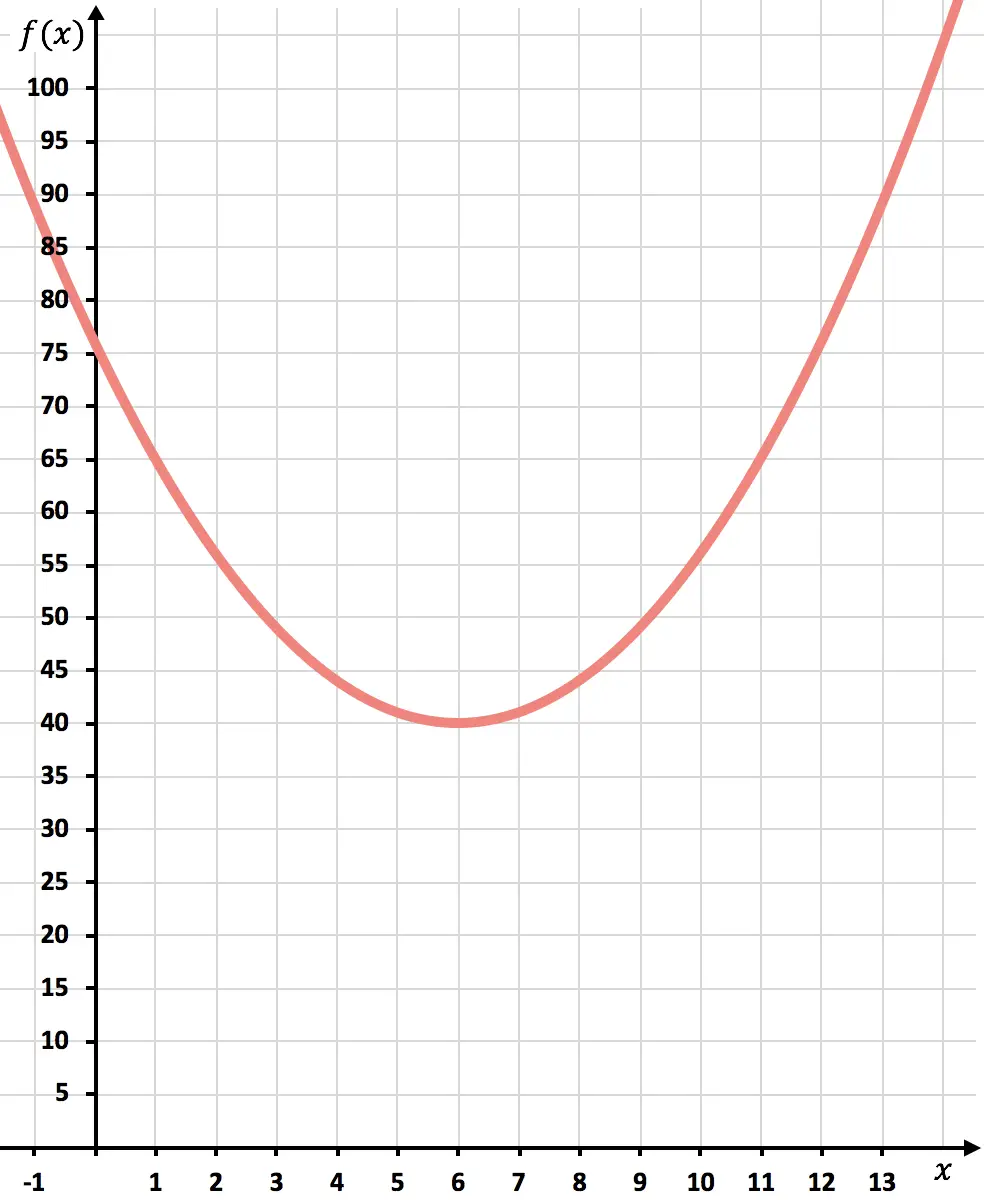
problema di funzione quadratica o parabolica

Una volta rappresentata la funzione vedremo quanto i costi sono minimizzati.

Come mostra il grafico, i costi minimi verranno raggiunti nella parte superiore della parabola. Perché è lì che la funzione assume il valore più piccolo.

In conclusione, i costi saranno minimizzati producendo 6.000 unità.

Esercizio 7

Risolvi il seguente problema sulla funzione quadratica:

Un atleta esegue un lancio del giavellotto la cui traiettoria può essere rappresentata dalla seguente funzione:

$h(x) = -0,025x^2+2x+2$

Oro

$x$

sono i metri percorsi dal giavellotto e

$h$

la sua altezza (anche in metri).

Qual è l’altezza massima che può raggiungere il giavellotto?

Vedi la soluzione

Questa è una funzione quadratica, quindi la traiettoria del giavellotto sarà una parabola.

Inoltre, poiché il coefficiente del termine quadratico è negativo (-0,025), la parabola avrà una forma a U rovesciata e i suoi rami andranno verso il basso. In tal modo il giavellotto raggiungerà la massima altezza in alto, poiché questo sarà il punto più alto della parabola.

Calcoliamo quindi l’ascissa del vertice della parabola con la formula:

$x = \cfrac{-b}{2a} = \cfrac{-2}{2\cdot (-0,025)} = \cfrac{-2}{-0,05} = 40$

E poi calcoliamo quanto sarà alto il giavellotto in quel punto valutando la funzione in

$x=40:$

$h(40) = -0,025\cdot (40)^2+2\cdot 40+2 = 42$

L’altezza massima che il giavellotto può raggiungere è quindi di 42 metri.

Esercizio 8

Risolvi il seguente problema relativo alle funzioni quadratiche:

I costi di produzione (in euro) di un’azienda sono definiti dalla seguente funzione:

$C(q)=40000+20q+q^2$

Oro

$q$

sono le unità prodotte.

E il prezzo di vendita di ciascuna unità è di 520 euro.

Quanto profitto otterrà l’azienda se venderà 150 unità?
Quante unità dovrebbero essere vendute per ottenere il massimo profitto?

Vedi la soluzione

L’azienda guadagna 520 euro per ogni unità venduta. Pertanto la funzione che definisce il reddito è:

$I(q)=520\cdot q = 520q$

Oro

$q$

sono le unità vendute.

Ma ci chiedono del profitto, cioè del reddito meno i costi. Sottraiamo quindi i ricavi meno i costi per ottenere la funzione che descrive il profitto dell’azienda:

$B(q)=I(q)-C(q)$

$B(q)=520q - (40000+20q+q^2)$

$B(q)=520q - 40000-20q-q^2$

$B(q)=-q^2 + 500q - 40000$

Una volta conosciuta la funzione che descrive il profitto dell’azienda, è sufficiente sostituire 150 nell’espressione della funzione per calcolare il profitto che l’azienda otterrà vendendo 150 unità:

$\begin{aligned} B(150) & =-(150)^2 + 500\cdot 150 - 40000 \\[2ex] & = -22500+75000 - 40000 \\[2ex] & = \bm{12500} \end{aligned}$

Quindi, vendendo 150 unità, l’azienda realizzerà un profitto di 12.500 euro.

La dichiarazione ci chiede anche di calcolare per quante unità si ottiene il massimo profitto.

La funzione che descrive il profitto è una funzione quadratica, quindi avrà la forma di una parabola. E poiché il coefficiente del termine quadratico è negativo (-1), la parabola avrà la forma di U rovesciata e i suoi rami andranno verso il basso. Pertanto, i guadagni massimi si otterranno nella parte superiore, poiché questo è il punto più alto della parabola.

Calcoliamo quindi l’ascissa del vertice della parabola con la formula:

$x = \cfrac{-b}{2a} = \cfrac{-500}{2\cdot(-1)} = \cfrac{-500}{-2} = 250$

Quindi l’azienda otterrà il massimo profitto vendendo 250 unità.

D’altra parte, anche se il comunicato stampa non lo richiede, possiamo determinare il profitto che si otterrà vendendo queste 250 unità:

$B(250) =-(250)^2 + 500\cdot250- 40000= 22500$

€

Funzione quadratica o parabola

Cos’è una funzione quadratica?

Concavità e convessità di una funzione quadratica

Vertice di una funzione quadratica

Punti di taglio con gli assi di una funzione quadratica

Esempio di rappresentazione di una funzione quadratica o parabolica

Esercizi risolti sulle funzioni quadratiche

Esercizio 1

Esercizio 2

Esercizio 3

Esercizio 4

Esercizio 5

Esercizio 6

Esercizio 7

Esercizio 8

Lascia un commento Annulla risposta