Funzione irrazionale o funzione radicale -

Questa pagina spiega cos’è una funzione irrazionale, detta anche funzione radicale, e tutte le caratteristiche di questo tipo di funzione. Scoprirai anche come calcolare il dominio delle funzioni radicali o irrazionali e, inoltre, potrai vedere come rappresentarle su un grafico con esempi ed esercitarti con esercizi e problemi risolti passo dopo passo.

Cos’è una funzione irrazionale (o radicale)?

Una funzione irrazionale ha lo stesso significato di una funzione radicale e, pertanto, condividono una definizione:

Una funzione irrazionale , detta anche funzione radicale , è una funzione che ha la variabile indipendente x sotto il simbolo di una radice.

Come già sappiamo, il risultato di una radice può essere positivo o negativo. Quindi la rappresentazione di una funzione irrazionale (o radicale) ha due possibili curve:

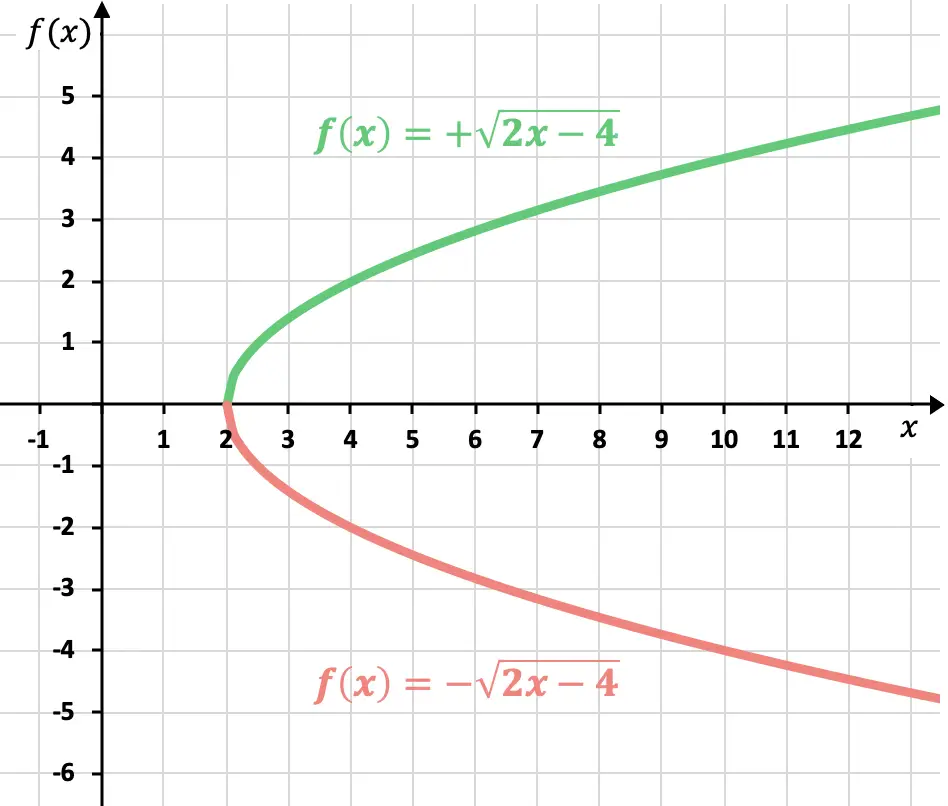
esempi di funzioni irrazionali o radicali

Ma se il segno non è specificato, si suppone che sia rappresentata la funzione positiva.

D’altra parte, una funzione irrazionale non deve essere confusa con una funzione razionale. Sebbene abbiano nomi molto simili, si tratta di due tipi di funzioni completamente diverse.

Dominio di una funzione irrazionale o radicale

Il dominio di una funzione con radici dipende dalla parità dell’indice radice, cioè dipende dal fatto che l’indice radicale sia pari o dispari.

Dominio di una funzione con radice di indice pari

Come ben sai, non esiste la radice (neppure l’indice) di un numero negativo. Pertanto, una funzione radicale con indice pari esisterà finché il suo contenuto sarà uguale o maggiore di 0.

Ad esempio, vediamo come viene calcolato il dominio della seguente funzione radicale o irrazionale:

$f(x)=\sqrt{x-4}$

Questa è una funzione di indice radicale pari, quindi dobbiamo guardare quando il suo contenuto è positivo o zero :

$x-4\ge 0$

Risolviamo la disuguaglianza:

$x\ge 4$

Quindi la funzione esisterà ogni volta che x è maggiore o uguale a 4 ed è indicata dal seguente intervallo:

$\text{Dom } f= [4,+\infty)$

Dominio di una funzione con radice di indice dispari

Le funzioni irrazionali con indice dispari non presentano questo problema, poiché esiste la radice dell’indice dispari di un numero negativo:

$\sqrt[3]{-8}=-2$

Pertanto, esistono funzioni radicali di indice dispari per qualsiasi valore di x . Ovvero, in altre parole, il dominio è formato solo da numeri reali .

Ad esempio, calcoleremo il dominio di definizione della seguente funzione radicale il cui indice è dispari:

$f(x)=\sqrt[3]{3x-4}$

Poiché è una funzione irrazionale con indice dispari, il suo dominio è costituito da numeri reali:

$\text{Dom } f= \mathbb{R}$

Come rappresentare una funzione irrazionale o radicale

Vediamo come rappresentare una funzione con radici su un grafico utilizzando un esempio.

Traccia su un grafico la seguente funzione radicale o irrazionale:

$f(x)=\sqrt{x+2}$

La prima cosa da fare è trovare il dominio della funzione. Poiché è una radice quadrata, tutto ciò che contiene deve essere positivo, poiché non esiste una radice quadrata di un numero negativo. Pertanto, la funzione radicale esisterà finché il suo contenuto sarà uguale o maggiore di 0:

$x+2\ge 0$

$x\ge -2$

Pertanto, il dominio della funzione è costituito da tutti i numeri maggiori o uguali a -2. Questo è da dire:

$\text{Dom } f = [-2,+\infty)$

Una volta conosciuto il dominio della funzione, creiamo una tabella di valori. Ovviamente, più punti calcoliamo, più precisa sarà la rappresentazione della funzione. Ma è sufficiente calcolare 3 o 4 punti nell’intervallo del dominio:

$x= -2 \ \longrightarrow \ f(-2)=\sqrt{-2+2}= 0$

$x= -1 \ \longrightarrow \ f(-1)=\sqrt{-1+2}= 1$

$x= 2 \ \longrightarrow \ f(2)=\sqrt{2+2}= 2$

$x= 7 \ \longrightarrow \ f(7)=\sqrt{7+2}= 3$

$\begin{array}{c|c} x & f(x) \\ \hline -2 & 0 \\ -1 & 1 \\ 2 & 2 \\ 7 & 3 \end{array}$

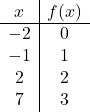
Rappresentiamo ora i punti ottenuti su un grafico :

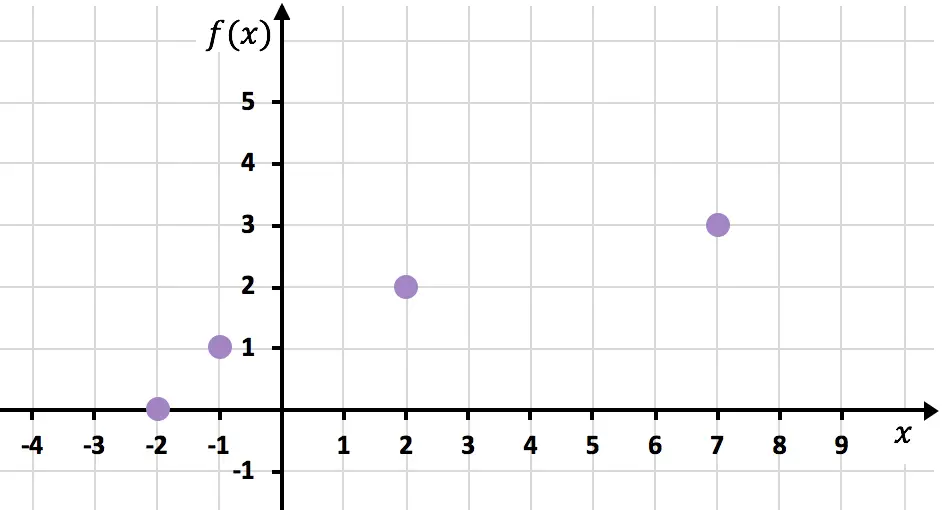
come rappresentare una funzione radicale o irrazionale

Infine uniamo i punti ed estendiamo la curva per indicare che la funzione continua a crescere:

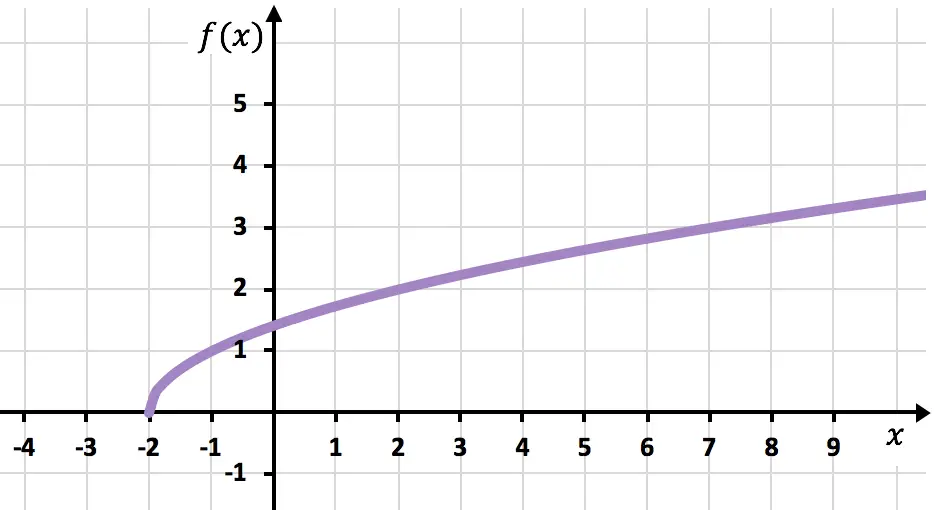
esempio di rappresentazione grafica di una funzione radicale o irrazionale

Esercizi risolti su funzioni irrazionali o radicali

Esercizio 1

Trova il dominio della seguente funzione radicale:

$\sqrt{3x+6}$

Vedi la soluzione

La radice quadrata di un numero negativo non esiste. Pertanto, la funzione esisterà quando l’argomento radice è positivo o zero:

$3x+6 \ge 0$

$3x \ge -6$

$x \ge \cfrac{-6}{3}$

$x \ge -2$

$\mathbf{Dom } \ \bm{f = [-2,+\infty)}$

Esercizio 2

Trova il dominio della seguente funzione irrazionale:

$\sqrt{-x+2}$

Vedi la soluzione

La radice quadrata di un numero negativo non ha soluzione reale. Pertanto, la funzione esisterà finché il contenuto della radice sarà positivo o zero:

$-x+2\ge 0$

$-x\ge -2$

$x\le\cfrac{-2}{-1}=2$

Ricorda che se in una disuguaglianza cambiamo i lati di un numero negativo che moltiplica o divide, dobbiamo ruotare anche il segno della disuguaglianza.

$x\le2$

$\mathbf{Dom } \ \bm{f = (-\infty,2]}$

Esercizio 3

Traccia su un grafico la seguente funzione irrazionale:

$f(x)= \sqrt{x-1}$

Vedi la soluzione

Innanzitutto dobbiamo calcolare il dominio della funzione:

$x-1\ge 0$

$x\ge 1$

$\text{Dom } f = [1,+\infty)$

Ora creiamo un array di valori fornendo i valori della funzione nell’intervallo di dominio:

$x= 1 \ \longrightarrow \ f(1)= \sqrt{1-1}=0$

$x= 2 \ \longrightarrow \ f(2)= \sqrt{2-1}=1$

$x= 5 \ \longrightarrow \ f(5)= \sqrt{5-1}=2$

$x= 10 \ \longrightarrow \ f(10)= \sqrt{10-1}=3$

$\begin{array}{c|c} x & f(x) \\ \hline 1 & 0 \\ 2 & 1 \\ 5 & 2 \\ 10 & 3 \end{array}$

Infine tracciamo i punti e tracciamo la funzione sul grafico:

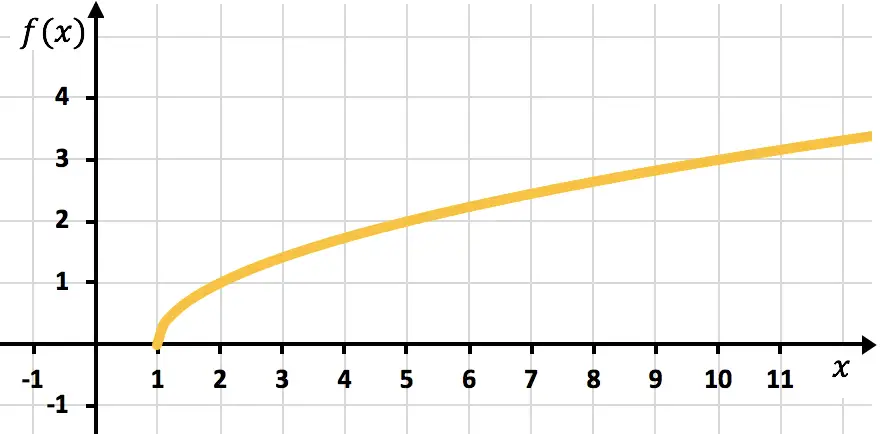
esercizio risolto passo dopo passo di una funzione irrazionale o radicale

Esercizio 4

Rappresentare graficamente la seguente funzione irrazionale o radicale:

$f(x)= -2\sqrt{x}+3$

Vedi la soluzione

Innanzitutto dobbiamo calcolare il dominio della funzione:

$x\ge 0$

$\text{Dom } f = [0,+\infty)$

Ora creiamo un array di valori fornendo i valori della funzione nell’intervallo di dominio:

$x= 0 \ \longrightarrow \ f(0)= -2\sqrt{0}+3=3$

$x= 1 \ \longrightarrow \ f(1)= -2\sqrt{1}+3=1$

$x= 4 \ \longrightarrow \ f(4)= -2\sqrt{4}+3=-1$

$x= 9 \ \longrightarrow \ f(9)= -2\sqrt{9}+3=-3$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 3 \\ 1 & 1 \\ 4 & -1 \\ 9 & -3 \end{array}$

Infine tracciamo i punti e disegniamo la funzione sul grafico:

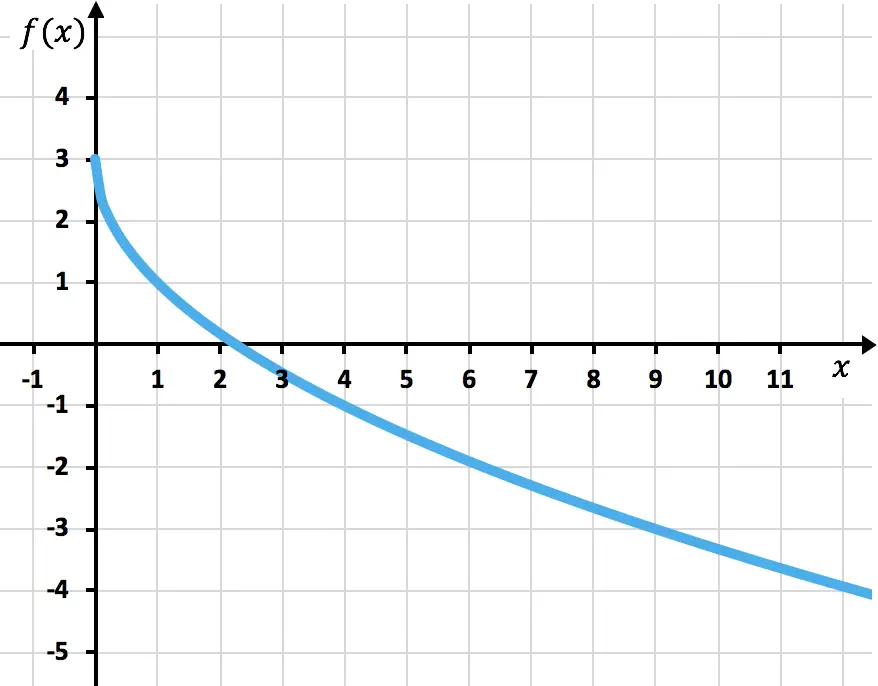
Esercizio 5

Rappresentare graficamente la seguente funzione irrazionale o radicale:

$f(x)= \sqrt{-x+5}$

Vedi la soluzione

Prima di tracciare la funzione, dobbiamo calcolare il dominio della funzione:

$-x+5\ge 0$

$-x\ge -5$

$x\le\cfrac{-5}{-1}=5$

Ricorda che se in una disuguaglianza cambiamo i lati di un numero negativo che moltiplica o divide, dobbiamo cambiare anche il segno della disuguaglianza.

$x\le5$

$\text{Dom } f = (-\infty,5]$

Ora costruiamo una tabella di valori valutando la funzione nei punti che appartengono al dominio della funzione:

$x= 5 \ \longrightarrow \ f(5)=\sqrt{-5+5}=0$

$x= 4 \ \longrightarrow \ f(4)=\sqrt{-4+5}=1$

$x= 1 \ \longrightarrow \ f(1)=\sqrt{-1+5}=2$

$x= -4 \ \longrightarrow \ f(-4)=\sqrt{-(-4)+5}=3$

$\begin{array}{c|c} x & f(x) \\ \hline 5 & 0 \\ 4 & 1 \\ 1 & 2 \\ -4 & 3 \end{array}$

E infine, rappresenta semplicemente i punti e dipingi la funzione sul grafico:

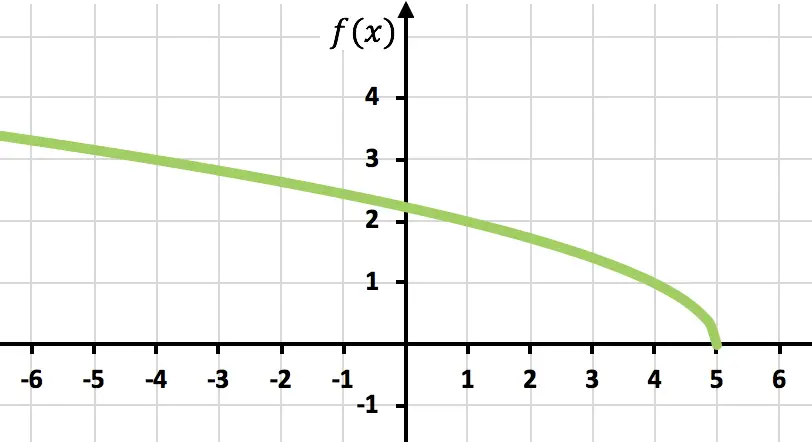
determinati esercizi di funzioni radicali o irrazionali

Esercizio 6

Traccia la seguente funzione irrazionale o radicale su un grafico:

$f(x)= \sqrt{x^2-5x+4}$

Vedi la soluzione

Dobbiamo prima calcolare il dominio della funzione:

$x^2-5x+4\ge 0$

In questo caso, abbiamo ottenuto una disuguaglianza di secondo grado, quindi dobbiamo applicare la formula delle equazioni quadratiche per risolverla:

$x=\cfrac{-b\pm \sqrt{b^2-4ac}}{2a}$

$\displaystyle x=\cfrac{-(-5)\pm \sqrt{(-5)^2-4\cdot 1\cdot 4}}{2\cdot 1} = \cfrac{5\pm 3}{2} =\begin{cases} 4 \\[2ex] 1 \end{cases}$

Dividiamo la linea in tre pezzi con le radici ottenute:

E sostituiamo un numero per ciascuna sezione della disuguaglianza, per vedere quali sezioni soddisfano la disuguaglianza e, quindi, appartengono al dominio:

$x^2-5x+4\ge 0 \ \xrightarrow{x\ = \ 0} <img src="https://mathority.org/wp-content/ql-cache/quicklatex.com-7c214e08b91825263231bc6eddbbdee1_l3.png" height="54" width="404" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[0^2-5\cdot 0+4\ge 0 \ \longrightarrow \ 4\ge 0 $ ✅$x^2-5x+4\ge 0 \ \xrightarrow{x\ = \ 2}\]" title="Rendered by QuickLaTeX.com"/> 2^2-5\cdot 2+4\ge 0 \ \longrightarrow \ -10\ \cancel{\ge } \ 0″ title=”Rendered by QuickLaTeX.com”> ❌ <p class=$ $x^2-5x+4\ge 0 \ \xrightarrow{x\ = \ 5}$

$5^2-5\cdot 5+4\ge 0 \ \longrightarrow \ 4\ge 0$

✅

Pertanto, le sezioni che rispettano la disuguaglianza sono quelle dei lati:

Il dominio della funzione è quindi:

$\text{Dom } f = (-\infty,1]\cup [4,+\infty)$

Una volta calcolato il dominio della funzione, costruiamo una tabella di valori che riporta i valori della funzione nell’intervallo del dominio:

$x= 1 \ \longrightarrow \ f(1)=\sqrt{1^2-5\cdot 1+4} =0$

$x= 0 \ \longrightarrow \ f(0)=\sqrt{0^2-5\cdot 0+4} =2$

$x= -1 \ \longrightarrow \ f(-1)=\sqrt{(-1)^2-5\cdot (-1)+4} =3,16$

$x= 4 \ \longrightarrow \ f(4)=\sqrt{4^2-5\cdot 4+4} =0$

$x= 5 \ \longrightarrow \ f(5)=\sqrt{5^2-5\cdot 5+4} =2$

$x= 6 \ \longrightarrow \ f(6)=\sqrt{6^2-5\cdot 6+4} =3,16$

$\begin{array}{c|c} x & f(x) \\ \hline 1 & 0 \\ 0 & 2 \\ -1 & 3,16 \\ 4 & 0 \\ 5 & 2 \\ 6 & 3,16 \\ \end{array}$

Infine, rappresentiamo i punti ottenuti sul grafico e tracciamo la funzione:

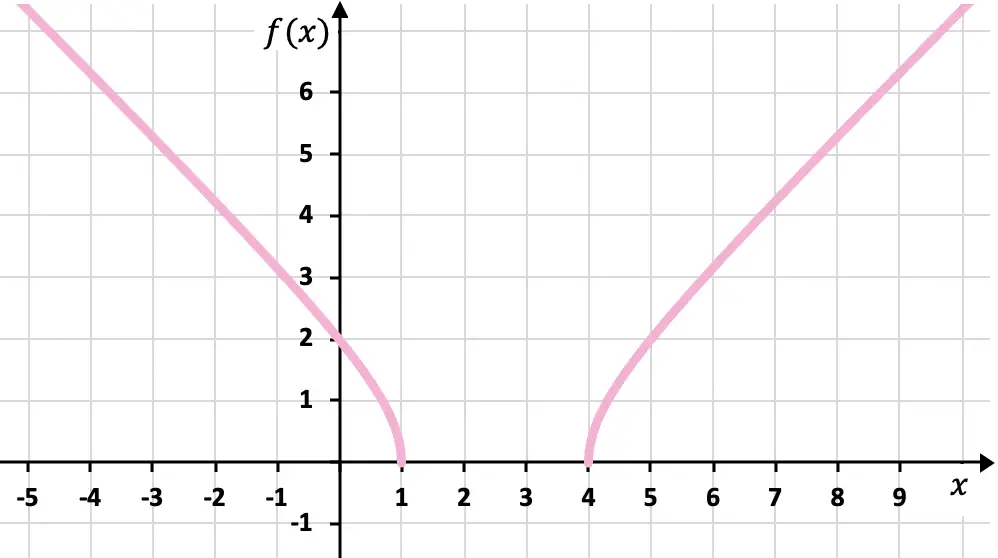
grafico di una funzione irrazionale o radicale con indice pari

Esercizio 7

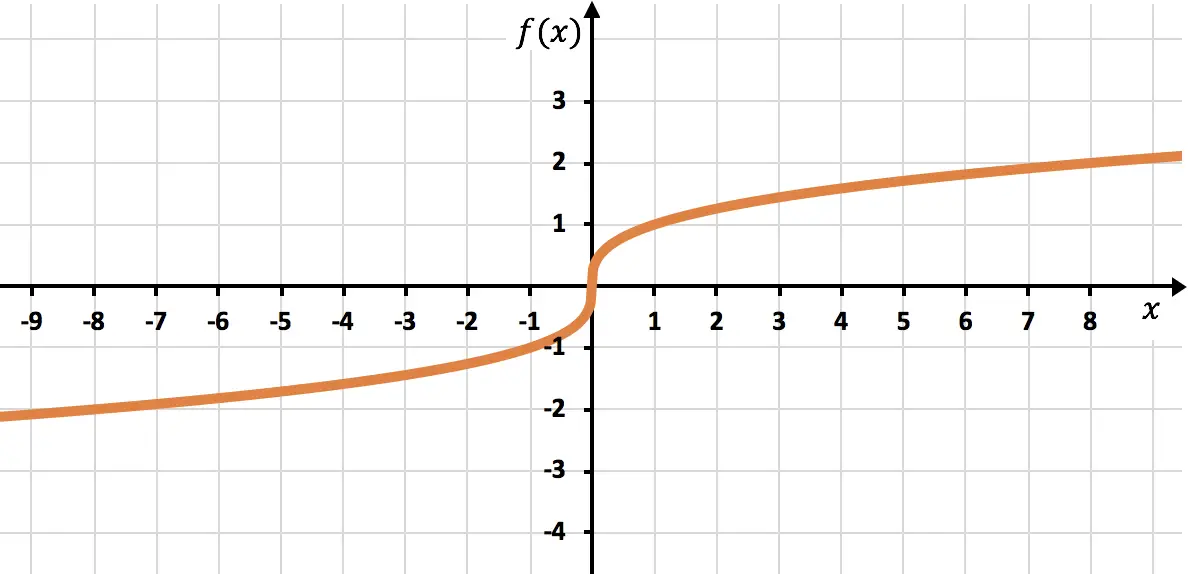
Rappresentate sul grafico la seguente funzione formata da una radice:

$f(x)= \sqrt[3]{x}$

Vedi la soluzione

È una funzione irrazionale la cui radice ha un indice dispari, quindi il dominio della funzione è costituito da numeri reali:

$\text{Dom } f = \mathbb{R}$

Possiamo quindi prendere qualsiasi punto per creare la tabella dei valori. In questo caso cercheremo molti punti perché è una radice cubica:

$x= 0 \ \longrightarrow \ f(0)= \sqrt[3]{0} = 0$

$x= 0,5 \ \longrightarrow \ f(0,5)= \sqrt[3]{0,5} = 0,79$

$x= -0,5 \ \longrightarrow \ f(-0,5)= \sqrt[3]{-0,5} = -0,79$

$x= 1 \ \longrightarrow \ f(1)= \sqrt[3]{1} = 1$

$x= -1 \ \longrightarrow \ f(-1)= \sqrt[3]{-1} = -1$

$x= 8 \ \longrightarrow \ f(8)= \sqrt[3]{8} = 2$

$x= -8 \ \longrightarrow \ f(-8)= \sqrt[3]{-8} = -2$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 0 \\ 0,5 & 0,79 \\ -0,5 & -0,79 \\ 1 & 1 \\ -1 & -1 \\ 8 & 2 \\ -8 & -2 \end{array}$

Infine, tracciamo i punti trovati e tracciamo la funzione sul grafico:

rappresentare graficamente una funzione irrazionale o radicale con un indice dispari

Esercizio 8

Risolvi il seguente problema relativo alle funzioni irrazionali (o radicali):

Il consumo della batteria di un cellulare è dato dalla seguente funzione:

$f(t)=\sqrt{x-K \vphantom{(-K)}}$

Dove il consumo è espresso in milliampere (mA) e

$t$

è il tempo trascorso in minuti.

Determinare il valore della costante

$K$

in modo che dopo 4 minuti il consumo sia di 35 mA.

Vedi la soluzione

Che dopo 4 minuti il consumo sia 35 mA significa che quando t è 4, f(t) è 35. Quindi f(4)=35.

$f(4)=\sqrt{4-K} = 35$

$\sqrt{4-K} = 35$

Ora dobbiamo risolvere l’equazione che abbiamo ottenuto. Se guardi da vicino, è un’equazione irrazionale poiché ha una radice. In questo tipo di equazioni la prima cosa da fare è isolare la radice di un membro, che in questo caso è già isolata. Una volta isolato, dobbiamo elevare al quadrato entrambi i lati dell’equazione:

$\left( \sqrt{4-K} \right)^2= 35^2$