Qui troverai qual è la funzione identità. Inoltre, potrai vedere come rappresentare graficamente la funzione identità e quali sono le sue caratteristiche.
Cos’è una funzione di identità?
Una funzione identità è quella funzione che ha come immagine lo stesso valore dell’argomento. La funzione identità può essere espressa con il termine id .
Pertanto, l’espressione matematica per la funzione identità è:
![]()
Ad esempio, l’immagine della funzione identità per x=1 vale 1, l’immagine di x=2 vale 2, l’immagine di x=3 vale 3,…
![Rendered by QuickLaTeX.com \begin{array}{c}f(1)=1\\[2ex]f(2)=2\\[2ex]f(3)=3\\ \bm{\vdots}\end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-4b85e48e3f36d1eb4271b265aaf35bef_l3.png)
La funzione identità è un esempio di funzione lineare. Nel seguente link puoi vedere altri esempi di questo tipo di funzioni:
➤ Vedi: esempi di funzioni lineari
Rappresentazione grafica della funzione identità
Il grafico della funzione identità corrisponde ad una linea che è la bisettrice del primo e del terzo quadrante.
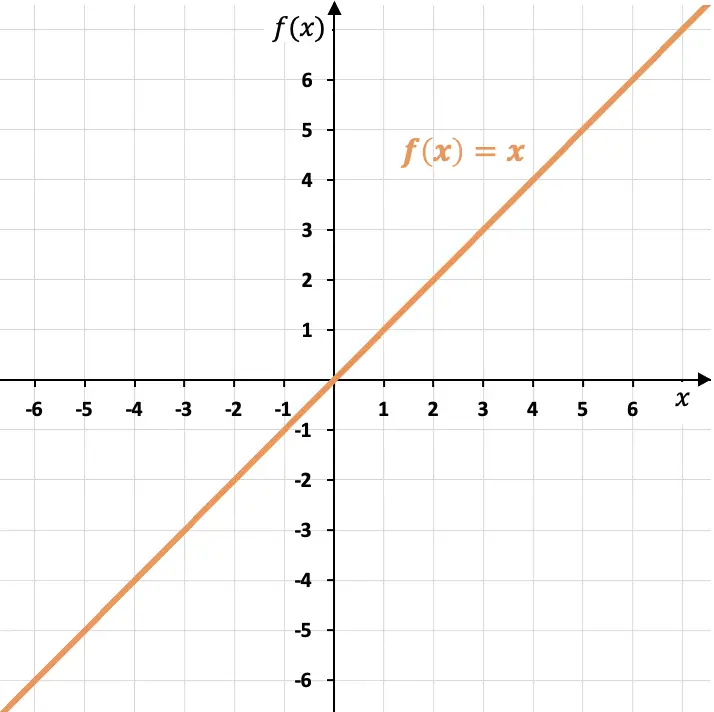
Come si vede, la funzione identità passa per l’origine delle coordinate (punto (0,0)) e ha pendenza pari all’unità (m=1), poiché aumenta un’unità della variabile e per ogni valore dell’indipendente variabile X. Inoltre, la funzione identità forma un angolo di 45º con l’asse X.
Caratteristiche della funzione identità
La funzione identità ha le seguenti proprietà:
- Il dominio della funzione identità è composto da tutti i numeri reali:
![]()
- Anche l’intervallo (o intervallo) della funzione identità è costituito da tutti i numeri reali:
![]()
- La funzione identità è una funzione continua e biiettiva.
- Inoltre, la funzione identità è costituita da una funzione dispari, il che significa che è una funzione simmetrica rispetto all’origine delle coordinate.
![]()
➤ Vedi: funzione simmetrica dispari
- La funzione identità è crescente su tutto il suo dominio e la sua pendenza è pari a 1.
![]()
- Interseca l’asse x (asse OX) e l’asse y (asse Y) nello stesso punto: l’origine delle coordinate.
![]()
- Può essere classificata come una funzione polinomiale di primo grado.
- La funzione identità funge da elemento neutrale della composizione della funzione . In modo che qualsiasi funzione composta con la funzione identità risulti nella funzione stessa.
![]()
- Il valore
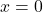
è l’unica radice di questo tipo di funzione.
- Il limite della funzione identità quando x tende a più infinito o meno infinito dà rispettivamente più infinito e meno infinito:
![]()
![]()
- La funzione identità quindi non ha asintoto.
- La derivata della funzione identità è la funzione costante con valore 1:
![]()
- L’integrale della funzione identità è la funzione quadratica:
![]()