▷ Fattoriale di un numero: cos'è e come calcolarlo ✅

Questa pagina spiega cos’è il fattoriale di un numero e come viene calcolato. Inoltre vengono presentati diversi esempi e una tabella con i valori dei fattoriali più utilizzati. Insegna anche come calcolare il fattoriale di un numero con la calcolatrice. Infine vengono illustrate le applicazioni e le proprietà dei fattoriali.

Qual è il fattoriale di un numero?

In matematica, il fattoriale di un numero è uguale al prodotto di tutti i numeri interi positivi da 1 a quel numero. Inoltre, il fattoriale di un numero è rappresentato da un punto esclamativo (!) dopo il numero.

Ad esempio, per determinare il fattoriale del numero n , chiamato anche fattoriale n , è necessario moltiplicare il numero n per tutti i numeri interi che lo precedono (a partire da uno):

$n! = 1 \cdot 2 \cdot 3 \cdots (n-2) \cdot (n-1) \cdot n$

Come calcolare il fattoriale di un numero

Una volta visto il significato del fattoriale di un numero, vediamo con un esempio come determinare un fattoriale qualsiasi:

Calcola il fattoriale di 4:

Come abbiamo visto nella sua definizione matematica, il fattoriale di un numero equivale alla moltiplicazione di tutti gli interi positivi minori o uguali ad esso. Pertanto, per calcolare il fattoriale di 4, dobbiamo moltiplicare i numeri 1, 2, 3 e 4:

$4! = 1 \cdot 2 \cdot 3 \cdot 4 =24$

Il fattoriale di 4 dà quindi 24.

Esempi di fattoriali di numeri

Per completare la comprensione della nozione di fattoriale di un numero, vi lasciamo con un esempio di calcolo di più fattoriali di numeri diversi:

Fattoriale di 3:

$3! = 1 \cdot 2 \cdot 3 =6$

Fattoriale di 5:

$5! = 1 \cdot 2 \cdot 3 \cdot 4 \cdot 5=120$

Fattoriale di 6:

$6! = 1 \cdot 2 \cdot 3 \cdot 4 \cdot 5 \cdot 6=720$

Fattoriale di 1:

$1! = 1$

Logicamente il fattoriale del numero 1 è uguale a 1, poiché è sufficiente moltiplicare 1.

Fattoriale di 0:

$0! = 1$

Sì, ok, sorprendentemente, il fattoriale di 0 non è uguale a zero, ma a 1. Questo può sembrarti un po’ strano, perché in teoria devi moltiplicare 0 per 1. Tuttavia, per convenzione è adottato che 0! =1 perché la proprietà del prodotto è vuota . Ti lasciamo questo link nel caso tu voglia saperne di più, anche se non è molto rilevante che tu ne conosca il motivo, l’importante è che ricordi che il fattoriale di 0 è uguale a 1 .

Elenco dei risultati per fattoriali di numeri

Di seguito abbiamo riassunto in una tabella i fattoriali dei numeri più utilizzati, così non dovrai calcolarli a mano.

Il numero	Fattoriale del numero
0	1
1	1
2	2
3	6
4	24
5	120
6	720
7	5.040
8	40.320
9	362.880
dieci	3.628.800
undici	39.916.800
12	479.001.600
13	6.227.020.800
14	87 178 291 200
quindici	1.307.674.368.000
16	20.922.789.888.000
17	355.687.428.096.000
18	6.402.373.705.728.000
19	121.645.100.408.832.000
venti	2.432.902.008 176.640.000
cinquanta	3.041.409.320 · ^10,64
100	9.332 621.544 · ^10.157
1.000	4.023.872.601 · ^10,2567
10.000	2.846.259.681 · ^10,35.659
100.000	2 824 229 408 · 10 ^{45 6573}
1.000.000	8.263.931.688 · 10 ^5.565.708

Fattoriale di un numero con la calcolatrice

Come puoi vedere negli esempi precedenti, i risultati dei fattoriali di due numeri consecutivi aumentano in modo esponenziale, motivo per cui è abbastanza difficile conoscere il fattoriale dei numeri grandi. Quindi ti mostreremo come trovare il fattoriale di un numero con la calcolatrice.

Le calcolatrici scientifiche hanno una chiave con il simbolo x! oppure no! che viene utilizzato per calcolare il fattoriale di un numero intero. Quindi, per determinare quanto vale un fattoriale, è necessario eseguire la seguente sequenza sulla calcolatrice:

$n! \quad \color{red} \bm{\longrightarrow} \quad \color{black} n\rightarrow \boxed{x!} \rightarrow \boxed{=}$

Normalmente le calcolatrici CASIO hanno la chiave fattoriale x! oppure no! sopra il pulsante x ^-1 .

Ad esempio, risolveremo un fattoriale con la calcolatrice in modo che tu possa verificare di sapere come farlo. Ad esempio, faremo il fattoriale di 9:

$9! \quad \color{red} \bm{\longrightarrow} \quad \color{black} 9\rightarrow \boxed{x!} \rightarrow \boxed{=} \rightarrow 362880$

Per trovare il fattoriale di 9 devi prima inserire il numero 9, quindi premere il tasto

$\boxed{x!}$

e infine, premere il pulsante uguale. In questo caso la calcolatrice dovrebbe mostrarci il risultato di 362.880.

Applicazioni del numero fattoriale

La funzione fattoriale di un numero può sembrare un’operazione molto semplice e assurda, ma nell’algebra avanzata viene utilizzata parecchio. Vedremo poi i principali utilizzi del fattoriale.

Innanzitutto il fattoriale è un’operazione essenziale per calcolare un numero combinatorio , un’operazione più che particolare. Se non sai cos’è il numero combinatorio, puoi vedere in cosa consiste e come si calcola in questo link, dove troverai esempi, esercizi risolti e quali sono le sue proprietà. Inoltre, sarai in grado di vedere a cosa serve poiché ha molte applicazioni nel mondo reale.

Il fattoriale viene utilizzato anche in matematica per determinare il polinomio di Taylor di una funzione.

Allo stesso modo, il fattoriale viene utilizzato per risolvere alcuni problemi combinatori, in particolare per calcolare combinazioni e permutazioni. In questo senso, i fattoriali vengono spesso utilizzati anche per calcolare le probabilità utilizzando la combinatoria.

Una permutazione di n elementi corrisponde a ciascuna delle diverse disposizioni che possono essere fatte con questi elementi. Quindi, per calcolare una permutazione, viene utilizzato il fattoriale. Ad esempio, se in un problema vuoi trovare il numero di possibilità in cui possono essere disposti 7 oggetti, devi calcolare il fattoriale di 7.

Vediamo ora un esercizio risolto:

Abbiamo 5 paia di scarpe diverse, in quanti modi possiamo sistemarle?

In questo esercizio dobbiamo scoprire tutti i modi possibili per abbinare queste 5 paia di scarpe tenendo conto dell’ordine in cui le mettiamo. Quindi per risolvere il problema basta calcolare il fattoriale di 5:

$5! = 1\cdot 2 \cdot 3\cdot 4\cdot 5 =120$

Insomma, le 5 paia di scarpe possono essere posizionate in 120 modi diversi.

Proprietà del numero fattoriale

Il numero fattoriale ha le seguenti caratteristiche:

Essendo due interi positivi n e m tali che n è maggiore di m , allora, ovviamente, il valore del fattoriale di n è maggiore del valore del fattoriale di m .

$n>m \quad \longrightarrow \quad n! > m!” title=”Rendered by QuickLaTeX.com” height=”15″ width=”183″ style=”vertical-align: -2px;”> <ul style=$

Il fattoriale di un numero può essere scomposto fattorialmente in modo che uno dei fattori sia il fattoriale di un numero più piccolo.

$n>m \quad \longrightarrow \quad n!= n\cdot (n-1) \cdots (m+1)\cdot m!” title=”Rendered by QuickLaTeX.com” height=”19″ width=”361″ style=”vertical-align: -5px;”> Ad esempio, 6 è maggiore di 4, quindi l’espressione per il fattoriale di 6 può essere semplificata come segue: <p class=$ $6! = 6 \cdot 5 \cdot 4!$

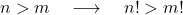
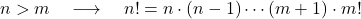
La seguente espressione algebrica è valida per il fattoriale di qualsiasi numero, eccetto il fattoriale di 1:

$\displaystyle n!< \left( \frac{n+1}{2} \right)^n$

Fattoriale di un numero negativo o decimale

Abbiamo appena visto come trovare il valore del fattoriale di un intero positivo, ma… possiamo calcolare il fattoriale di un numero negativo o di un numero decimale? La risposta è sì, ma è richiesta una conoscenza avanzata della matematica.

Il fattoriale di un numero negativo e di un numero decimale viene calcolato utilizzando una funzione speciale chiamata “funzione Gamma” di Eulero, definita dal seguente integrale:

$\displaystyle \Gamma(z)=\int_0^\infty t^{z-1} e^{-t}\, \mathrm{d}t$

Pertanto qualsiasi tipo di fattoriale può essere risolto con la funzione Gamma perché la seguente equazione è sempre vera:

$n! = \Gamma(n+1)$

Quindi per trovare il fattoriale di 0,5, ad esempio, dobbiamo trovare il valore di

$\Gamma(1,5)$

Perché:

$0,5! = \Gamma(0,5+1) =\Gamma(1,5)$

E la soluzione dell’integrale corrisponderà al fattoriale di 0,5.

Ovviamente risolvere l’integrale della funzione Gamma non è facile e non lo insegneremo in questo articolo, perché molti concetti matematici andrebbero spiegati prima. Volevamo però farti sapere che esiste la possibilità di calcolare il fattoriale di un numero negativo o di un numero decimale.

Infatti, a titolo di esempio, abbiamo calcolato alcuni valori fattoriali e decimali negativi:

$\underline{\bm{n}}$	$\underline{\bm{n!}}$
$\displaystyle \left(\frac{1}{2}\right)!$	$\displaystyle \frac{1}{2}\sqrt{\pi}$
$\displaystyle \left(-\frac{1}{2}\right)!$	$\displaystyle \sqrt{\pi}$
$\displaystyle \left(\frac{3}{2}\right)!$	$\displaystyle \frac{3}{4}\sqrt{\pi}$
$\displaystyle \left(\frac{5}{2}\right)!$	$\displaystyle \frac{15}{8}\sqrt{\pi}$