Funzioni esponenziali: caratteristiche, rappresentazione grafica, esercizi,...

In questa pagina scoprirai cosa sono le funzioni esponenziali e anche come rappresentare una funzione esponenziale su un grafico. Inoltre vedrai tutte le sue caratteristiche e diversi esempi per comprenderlo appieno. Infine, potrai esercitarti con esercizi e problemi risolti passo dopo passo sulle funzioni esponenziali.

Cos’è una funzione esponenziale?

La definizione di funzione esponenziale è la seguente:

In matematica, le funzioni esponenziali sono funzioni che hanno la variabile indipendente x nell’esponente di una potenza. In altre parole, sono i seguenti:

$f(x)=a^x$

Oro

$a$

è un numero reale positivo e diverso da 1.

Esempi di funzioni esponenziali

Le seguenti funzioni sono esempi di funzioni esponenziali:

$f(x)=3^{x}$

$f(x)=4^{-x}$

$\displaystyle f(x)=\left( \frac{1}{2} \right)^x$

$f(x)=5^x$

Caratteristiche delle funzioni esponenziali

Le funzioni esponenziali hanno le seguenti proprietà:

Il dominio di una funzione esponenziale è costituito da numeri reali o, in altre parole, esiste una funzione esponenziale per qualsiasi valore di x .

$\text{Dom } f=\mathbff{R}$

Tuttavia, la funzione accetta solo valori positivi, quindi l’intervallo di una funzione esponenziale è costituito da numeri reali positivi.

$\text{Im } f= (0,+\infty)$

Ogni funzione esponenziale è sia una funzione continua che una funzione iniettiva.

Se la funzione non viene tradotta, qualsiasi funzione esponenziale passa per il punto (0,1). Perché la funzione valutata a zero dà sempre uno.

$f(0)=a^0=1$

Allo stesso modo, il valore di una funzione esponenziale in x=1 è uguale alla base.

$f(1)=a^1=a$

Se la base di potere
$(a)$

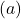
è maggiore di 1, la funzione esponenziale è crescente. D’altra parte, se il coefficiente

$a$

è nell’intervallo tra 0 e 1, la funzione esponenziale è decrescente.

In generale, l’asse x è un asintoto orizzontale di una funzione esponenziale.

L’inverso della funzione esponenziale è la funzione logaritmica. Pertanto, i grafici di una funzione esponenziale e di una funzione logaritmica sono simmetrici rispetto alla retta y=x se entrambi hanno la stessa base.

Come rappresentare graficamente una funzione esponenziale

Le funzioni esponenziali sono molto semplici da rappresentare. Vediamo quindi come rappresentare graficamente una funzione esponenziale su un grafico utilizzando un esempio.

Traccia la seguente funzione esponenziale su un grafico:

$f(x)=2^x$

Nelle funzioni esponenziali non è necessario calcolare il dominio, perché saranno sempre tutti numeri reali:

$\text{Dom } f = \mathbb{R}$

È quindi sufficiente stilare la tabella dei valori. Poiché questi tipi di funzioni cambiano molto da un punto all’altro, calcoleremo 5 punti. Ma più punti calcoliamo, più precisa sarà la rappresentazione della funzione.

$x= 0 \ \longrightarrow \ f(0)=2^0= 1$

$x= 1 \ \longrightarrow \ f(1)=2^1= 2$

$x= 2 \ \longrightarrow \ f(2)=2^2= 4$

$x= -1 \ \longrightarrow \ f(-1)=2^{-1}= 0,5$

$x= -2 \ \longrightarrow \ f(-2)=2^{-2}= 0,25$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 1 \\ 1 & 2 \\ 2 & 4 \\ -1 & 0,5 \\ -2 & 0,25 \end{array}$

Ti consigliamo di utilizzare una calcolatrice per trovare i punti nella tabella dei valori, poiché sono complicati da calcolare a mano.

Ora rappresentiamo i punti su un grafico :

E infine, uniamo i punti ed estendiamo la funzione:

come rappresentare o rappresentare graficamente una funzione esponenziale

Nota che la funzione a destra continua a crescere fino all’infinito.

Al contrario, la funzione di sinistra diminuisce ma non raggiunge mai lo 0. Anche se si avvicina molto ad esso, non lo tocca mai. Ciò significa che la linea y=0 (l’asse x) è un asintoto orizzontale.

Esercizi risolti su funzioni esponenziali

Esercizio 1

Rappresentare graficamente la seguente funzione esponenziale:

$f(x)= 2^x+1$

Vedi la soluzione

È una funzione esponenziale, quindi per rappresentarla è necessario creare una tabella di valori dando valori alla variabile x:

$x= 0 \ \longrightarrow \ f(0)= 2^0+1=2$

$x= 1 \ \longrightarrow \ f(1)= 2^1+1=3$

$x= 2 \ \longrightarrow \ f(2)= 2^2+1=5$

$x= -1 \ \longrightarrow \ f(-1)= 2^{-1}+1=1,5$

$x= -2 \ \longrightarrow \ f(-2)= 2^{-2}+1=1,25$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 2 \\ 1 & 3 \\ 2 & 5 \\ -1 & 1,5 \\ -2 & 1,25 \end{array}$

Una volta ottenuta la tabella dei valori, tracciamo i punti ottenuti sul grafico e tracciamo la funzione:

esercizio risolto passo passo di funzioni esponenziali

Nota che la funzione a destra continua a crescere fino all’infinito. A sinistra, invece, la funzione diminuisce ma non supera mai 1. A destra, infatti, la funzione ha un asintoto orizzontale y=1.

In questo caso l’asintoto orizzontale è in y=1 invece che sull’asse OX perché è stata fatta una traslazione verticale di una unità verso l’alto verso la funzione.

Esercizio 2

Traccia la seguente funzione esponenziale su un grafico:

$\displaystyle f(x)= \left(\frac{1}{3}\right)^x$

Vedi la soluzione

È una funzione esponenziale, quindi per rappresentarla graficamente è necessario costruire una tabella di valori dando valori alla variabile x:

$x= 0 \ \longrightarrow \ f(0)= \left(\cfrac{1}{3}\right)^0 = 1$

$x= 1 \ \longrightarrow \ f(1)= \left(\cfrac{1}{3}\right)^1 = 0,33$

$x= 2 \ \longrightarrow \ f(2)= \left(\cfrac{1}{3}\right)^2 = 0,11$

$x= -1 \ \longrightarrow \ f(-1)= \left(\cfrac{1}{3}\right)^{-1} = 3$

$x= -2 \ \longrightarrow \ f(-2)= \left(\cfrac{1}{3}\right)^{-2} = 9$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 1 \\ 1 & 0,33 \\ 2 & 0,11 \\ -1 & 3 \\ -2 & 9 \end{array}$

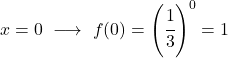
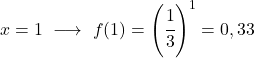
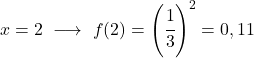
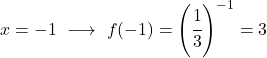
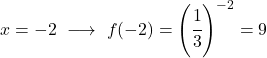
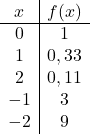
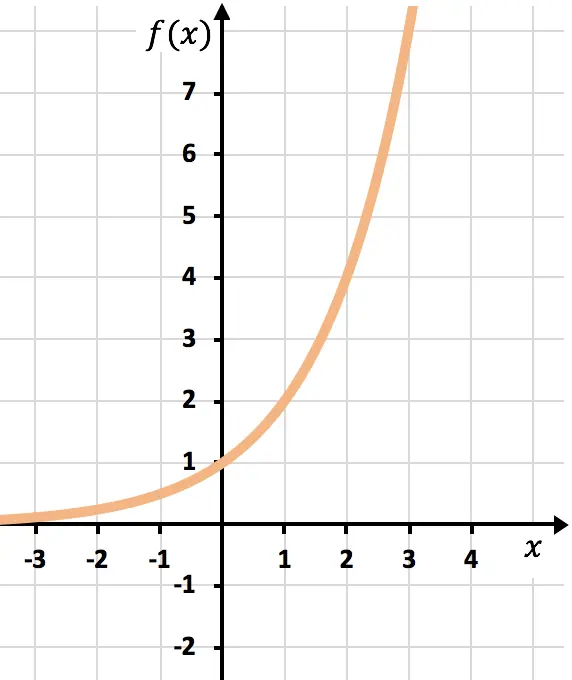
Una volta ottenuta la tabella dei valori, tracciamo i punti calcolati sul grafico e disegniamo la funzione:

Esercizi sulle funzioni esponenziali risolti

Nota che la funzione a sinistra continua a crescere fino all’infinito. D’altra parte, a destra, la funzione diminuisce ma non supera mai 0. Infatti, la funzione ha un asintoto orizzontale in y=0 (l’asse X).

Esercizio 3

Traccia la seguente funzione esponenziale su un grafico:

$\displaystyle f(x)= \left(\frac{1}{2}\right)^x+3$

Vedi la soluzione

È una funzione esponenziale, quindi per disegnarla è necessario creare una tabella di valori valutando la funzione in più punti:

$x= 0 \ \longrightarrow \ f(0)= \left(\cfrac{1}{2}\right)^0+3 = 4$

$x= 1 \ \longrightarrow \ f(1)= \left(\cfrac{1}{2}\right)^1+3 = 3,5$

$x= 2 \ \longrightarrow \ f(2)= \left(\cfrac{1}{2}\right)^2+3 = 3,25$

$x= -1 \ \longrightarrow \ f(-1)= \left(\cfrac{1}{2}\right)^{-1}+3 = 5$

$x= -2 \ \longrightarrow \ f(-2)= \left(\cfrac{1}{2}\right)^{-2}+3 = 7$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 4 \\ 1 & 3,5 \\ 2 & 3,25 \\ -1 & 5 \\ -2 & 7 \end{array}$

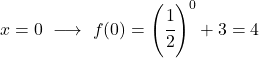
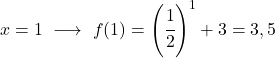
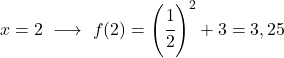
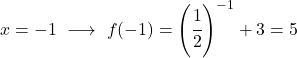
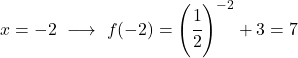
Infine, rappresentiamo i punti ottenuti sul grafico e tracciamo la funzione:

Nota che la funzione a sinistra cresce illimitatamente fino all’infinito. A destra, invece, la funzione diminuisce ma non supera mai 3. La funzione ha infatti un asintoto orizzontale in y=3.

In questo caso, l’asintoto orizzontale è su y=3 invece che sull’asse X perché la funzione è stata spostata verticalmente di tre unità verso l’alto.

Esercizio 4

Risolvi il seguente problema relativo alle funzioni esponenziali.

Determinare il valore di
$k$

in modo che la successiva funzione esponenziale passi per il punto (2.8).

$f(x)=k\cdot 2^x$

Vedi la soluzione

La funzione deve passare per il punto (2,8), quindi possiamo sostituire i valori di x e f(x) del punto nella funzione per trovare il valore della costante k:

$f(x)=k\cdot 2^x \ \xrightarrow{x \ = \ 2 \ ; \ f(x) \ = \ 8} \ 8 = k \cdot 2^2$

E ora risolviamo l’equazione risultante:

$8 = k \cdot 2^2$

$8 = k \cdot 4$

$\cfrac{8}{4} = k$

$\bm{ 2 = k}$

Esercizio 5

Risolvi il seguente problema relativo alle funzioni esponenziali.

Una popolazione di termiti si riproduce secondo la seguente funzione:

$f(t)=3^{t+1}$

Oro

$f(t)$

è il numero di termiti e

$t$

il tempo è passato da mesi.

Quante termiti ci saranno dopo 1 anno?

Vedi la soluzione

Per calcolare il numero di termiti che ci saranno in un anno, sostituisci semplicemente il tempo trascorso (1 anno) nella funzione. Ma poiché la funzione t rappresenta i mesi trascorsi e non gli anni, dobbiamo porre t = 12 poiché in un anno ci sono 12 mesi:

$f(t)=3^{t+1}$

$f(12)=3^{12+1}$

$f(12)=3^{13}$

Risolviamo con la calcolatrice:

$f(12)= 1594323$

Quindi dopo un anno ci saranno 1.594.323 termiti.

Funzione esponenziale

Cos’è una funzione esponenziale?

Esempi di funzioni esponenziali

Caratteristiche delle funzioni esponenziali

Come rappresentare graficamente una funzione esponenziale

Esercizi risolti su funzioni esponenziali

Esercizio 1

Esercizio 2

Esercizio 3

Esercizio 4

Esercizio 5

Lascia un commento Annulla risposta