In questo articolo spieghiamo cosa sono le funzioni di proporzionalità diretta, qual è la loro formula, come rappresentarle in un grafico e come calcolare la loro equazione a partire da un dato punto.
Cos’è una funzione di proporzionalità diretta?
La funzione di proporzionalità diretta è una funzione che mette in relazione due quantità direttamente proporzionali. Pertanto, per calcolare il valore della variabile dipendente (y), il valore della variabile dipendente (x) deve essere moltiplicato per la costante di proporzionalità.
La funzione di proporzionalità diretta è anche chiamata funzione lineare.
Ricorda che due quantità sono direttamente proporzionali se una quantità aumenta di valore mentre aumenta anche l’altra quantità, e viceversa.
Formula per la funzione di proporzionalità diretta
La formula che definisce la funzione di proporzionalità diretta è la seguente:
![]()
dove y è la variabile indipendente, x è la variabile dipendente e ym è la pendenza o costante di proporzionalità della funzione.
Come puoi vedere, con questa formula è molto semplice calcolare i valori della grandezza y, basta moltiplicare il valore della grandezza x per la pendenza della funzione, caratteristica di ciascuna funzione di proporzionalità diretta.
Ad esempio, se abbiamo la seguente funzione di proporzionalità diretta:
![]()
Se vogliamo determinare quanto vale la quantità y quando x è 5, dobbiamo solo moltiplicare la pendenza della funzione (3) per 5:
![]()
Rappresentazione grafica di una funzione di proporzionalità diretta
Successivamente vedremo come rappresentare graficamente le funzioni di proporzionalità diretta. Faremo il seguente esercizio come esempio:
![]()
Per rappresentare la funzione di proporzionalità diretta su un grafico è sufficiente tracciare una linea passante per l’ origine delle coordinate (punto (0,0)) e avente la pendenza della funzione.
In questo caso la funzione che vogliamo rappresentare ha pendenza pari a
![]()
Pertanto la linea deve crescere di due unità di y per ogni unità di x.
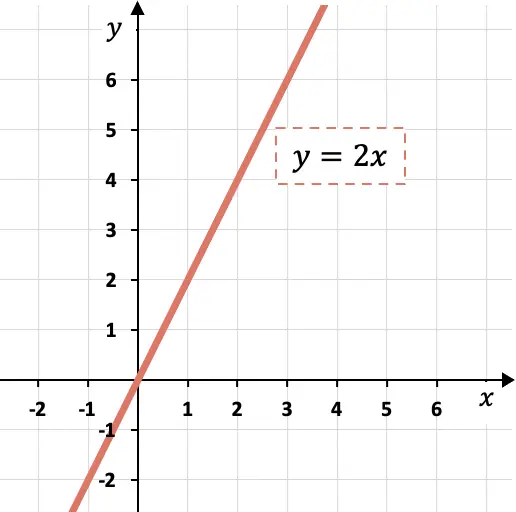
Come puoi vedere dal grafico, se la pendenza è pari a 2, ciò significa che la grandezza y aumenta il doppio della grandezza x.
Le funzioni di proporzionalità diretta hanno un grafico molto simile alle funzioni affini, ma sono due diversi tipi di funzioni. Puoi vedere quali sono le differenze tra una funzione affine e una funzione lineare nel seguente link:
➤ Vedi: differenza tra funzione lineare e affine
Come trovare la funzione di proporzionalità diretta
Se conosciamo un punto della funzione di proporzionalità diretta, possiamo facilmente trovarne l’equazione. Vediamo come si fa risolvendo un problema di funzione di proporzionalità diretta:
- Il numero di stanze che un pittore dipinge è approssimativamente direttamente proporzionale alle ore che lavora, cioè più ore lavora, più stanze può dipingere. Se sappiamo che in una giornata di 8 ore ha dipinto due intere stanze, qual è la funzione di proporzionalità diretta che mette in relazione il numero di stanze dipinte con le ore lavorate?
Innanzitutto dobbiamo determinare quale è la variabile dipendente e quale è quella indipendente. Il numero di pezzi dipinti dipende dalle ore lavorate e non viceversa. Pertanto, la variabile indipendente (x) è il numero di ore lavorate e la variabile dipendente (y) è il numero di stanze dipinte.
Il problema ci dice che il pittore può dipingere 2 stanze in 8 ore, quindi il grafico della funzione deve passare per il punto (8,2).
![]()
Inoltre, la dichiarazione indica che le due quantità hanno una relazione proporzionale diretta, il che significa che sono matematicamente correlate alla formula della funzione di proporzionalità diretta:
![]()
Possiamo ora calcolare il valore della pendenza della funzione sostituendo le coordinate del punto (8,2) nell’equazione:
![]()
E, infine, risolviamo l’incognita m dell’equazione:
![]()
![]()
![]()
In breve, la funzione di proporzionalità diretta del problema è:
![]()
Potrebbe piacerti anche: