▷ Concavità e convessità di una funzione (curvatura)

Qui imparerai cosa sono la concavità e la convessità di una funzione e come capire se una funzione è concava o convessa. Inoltre, potrai esercitarti con esercizi passo passo sulla curvatura di una funzione.

Che cosa sono la concavità e la convessità di una funzione?

La concavità e la convessità di una funzione si riferiscono alla curvatura del grafico di una funzione. Una funzione concava è una funzione il cui grafico ha la forma di una montagna, mentre una funzione convessa è una funzione il cui grafico ha la forma di una valle.

Nel paragrafo precedente, le funzioni concava e convessa sono state definite in modo informale per facilità di comprensione, ma la definizione matematica di funzione concava e funzione convessa è la seguente:

Funzione concava: quando il segmento che unisce due punti qualsiasi della funzione è al di sotto della curva.
Funzione convessa: quando il segmento che unisce due punti qualsiasi della funzione è al di sopra della curva.

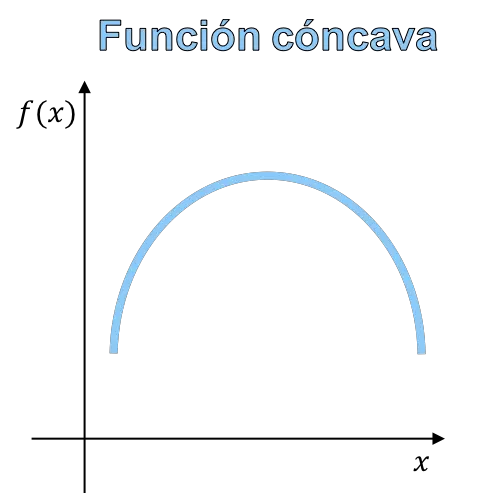
In definitiva, la differenza tra una funzione concava e una funzione convessa risiede nella forma della funzione e quindi è possibile distinguere la concavità dalla convessità dal grafico della funzione.

Tuttavia, una funzione non deve necessariamente essere concava o convessa su tutto il suo dominio, ma può anche essere concava su un intervallo e convessa su un altro intervallo.

Nota: La comunità matematica non è ancora del tutto d’accordo e, quindi, alcuni professori dicono il contrario: chiamano concava una funzione che ha la forma di un

$\bm{\cup}$

, e una funzione convessa che ha la forma di

$\bm{\cap}$

. In ogni caso l’importante è sapere qual è la funzione, qualunque sia il nome.

Come studiare la curvatura di una funzione

Studiare la curvatura di una funzione implica trovare la concavità e la convessità della funzione, cioè conoscere gli intervalli in cui la funzione è concava e gli intervalli in cui la funzione è convessa.

Quindi, per studiare la curvatura di una funzione, è necessario eseguire i seguenti passaggi:

Trova i punti che non appartengono al dominio della funzione.
Calcolare la derivata prima e la derivata seconda della funzione.
Trova le radici della derivata seconda , cioè calcola i punti che annullano la derivata seconda risolvendo
$f''(x)=0$

.
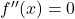
Crea intervalli con le radici della derivata e i punti che non appartengono al dominio della funzione.
Calcola il valore della derivata seconda in un punto di ciascun intervallo.
Pertanto, il segno della derivata seconda determina la concavità o convessità della funzione in questo intervallo:
- Se la derivata seconda della funzione è positiva, la funzione è convessa su questo intervallo.
- Se la derivata seconda della funzione è negativa, la funzione è concava su questo intervallo.

Esempio di come trovare la curvatura di una funzione

Successivamente, risolveremo un esempio passo dopo passo in modo da poter vedere come vengono calcolati gli intervalli di concavità e convessità di una funzione.

Studiare la concavità e la convessità della seguente funzione:

$f(x)=x^3-3x$

La prima cosa da fare è calcolare il dominio di definizione della funzione. In questo caso abbiamo una funzione polinomiale, quindi il dominio della funzione è costituito da numeri reali:

$\text{Dom } f= \mathbb{R}$

Una volta calcolato il dominio della funzione, dobbiamo indagare in quali punti la derivata seconda della funzione svanisce.

Calcoliamo quindi la derivata prima della funzione:

$f(x)=x^3-3x \ \longrightarrow \ f'(x)= 3x^2-3$

Troviamo quindi la derivata seconda della funzione:

$f'(x)=3x^2-3 \ \longrightarrow \ f''(x)= 6x$

E ora impostiamo la derivata seconda uguale a 0 e risolviamo l’equazione:

$f''(x)=0$

$6x=0$

$x=\cfrac{0}{6}$

$x=0$

Una volta calcolato il dominio della funzione e

$f''(x)=0$

, rappresentiamo tutti i punti critici presenti sulla retta. In questo caso non abbiamo trovato alcun punto critico nel calcolo del dominio di definizione della funzione, ma abbiamo ottenuto un punto che annulla la derivata seconda della funzione:

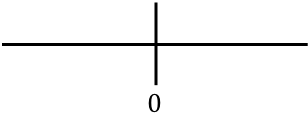
E ora valutiamo il segno della derivata seconda in ogni intervallo, per sapere se la funzione è concava o convessa. Prendiamo quindi un punto in ogni intervallo (mai i punti critici) e guardiamo che segno ha la derivata seconda in questo punto:

$f''(x)=6x$

$f''(-1) = 6\cdot (-1)=-6 \ \rightarrow \ \bm{-}$

$f''(1) = 6\cdot 1=+6 \ \rightarrow \ \bm{+}$

Infine, deduciamo gli intervalli di concavità e convessità della funzione. Se la derivata seconda è positiva significa che la funzione è convessa.

$(\bm{\cup})$

, e se la derivata seconda è negativa significa che la funzione è concava

$(\bm{\cap})$

. Pertanto gli intervalli di concavità e convessità della funzione sono:

Convesso

$(\bm{\cup})$

$\bm{(0,+\infty)}$

Concavo

$(\bm{\cap})$

$\bm{(-\infty,0)}$

Esercizi risolti sulla concavità e convessità di una funzione

Esercizio 1

Calcola gli intervalli di concavità e convessità della seguente funzione polinomiale:

$f(x) = x^3-3x^2-2x$

Vedi la soluzione

La funzione nell’esercizio è un polinomio, quindi il dominio della funzione è costituito da numeri reali:

$\text{Dom } f= \mathbb{R}$

Dopo aver determinato il dominio della funzione, lo differenziamo:

$f(x)=x^3-3x^2-2x \ \longrightarrow \ f'(x)= 3x^2-6x-2$

Troviamo quindi la derivata seconda della funzione:

$f'(x)= 3x^2-6x-2 \ \longrightarrow \ f''(x)= 6x-6$

E ora impostiamo la derivata seconda uguale a 0 e risolviamo l’equazione:

$f''(x)= 0$

$6x-6= 0$

$6x= 6$

$x= \cfrac{6}{6}$

$x=1$

Una volta calcolato il dominio della funzione e risolto

$f''(x)=0$

, rappresentiamo tutti i punti singolari presenti sulla retta numerica:

E ora prendiamo un punto appartenente a ciascun intervallo e vediamo che segno ha la derivata seconda in questo punto:

$f''(0)= 6\cdot 0-6 = -6 \ \rightarrow \ \bm{-}$

$f''(2)= 6\cdot 2-6 = 12-6=+6 \ \rightarrow \ \bm{+}$

Quando la derivata seconda è maggiore di zero significa che la funzione è convessa.

$(\bm{\cup})$

, ma quando la derivata seconda è negativa ciò implica che la funzione è concava

$(\bm{\cap})$

. Pertanto gli intervalli di concavità e convessità sono:

Convesso

$(\bm{\cup})$

$\bm{(1,+\infty)}$

Concavo

$(\bm{\cap})$

$\bm{(-\infty,1)}$

Esercizio 2

Studiare la curvatura della seguente funzione razionale:

$\displaystyle f(x)=\frac{x^3}{x^2-4}$

Vedi la soluzione

Per prima cosa dobbiamo calcolare il dominio della funzione. Trattandosi di una funzione razionale, poniamo il denominatore uguale a zero per vedere quali numeri non appartengono al dominio della funzione:

$x^2-4= 0$

$x^2=4$

$\sqrt{x^2}=\sqrt{4}$

$x=\pm 2$

Ciò significa che quando x è -2 o +2, il denominatore sarà 0. E quindi la funzione non esisterà. Il dominio della funzione è quindi composto da tutti i numeri tranne x=-2 e x=+2.

$\text{Dom } f= \mathbb{R}-\{-2, +2 \}$

In secondo luogo, calcoliamo la derivata prima della funzione:

$f(x)=\cfrac{x^3}{x^2-4} \ \longrightarrow \ f'(x)= \cfrac{3x^2 \cdot (x^2-4) - x^3 \cdot 2x }{\left(x^2-4\right)^2}$

$f'(x)= \cfrac{3x^4-12x^2-2x^4}{\left(x^2-4\right)^2} = \cfrac{x^4-12x^2}{\left(x^2-4\right)^2}$

E poi risolviamo la derivata seconda:

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^2 - \left(x^4-12x^2\right)\cdot 2\left(x^2-4\right)\cdot 2x }{ \left(\left(x^2-4\right)^2 \right)^2}$

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^2 - \left(x^4-12x^2\right)\cdot 4x\left(x^2-4\right) }{\left(x^2-4\right)^4 }$

Tutti i termini vengono moltiplicati per

$(x^2-4)$

. Possiamo quindi semplificare la frazione:

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^{\cancel{2}} - \left(x^4-12x^2\right)\cdot 4x\cancel{\left(x^2-4\right)} }{\left(x^2-4\right)^{\cancelto{3}{4}} }$

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right) - \left(x^4-12x^2\right)\cdot 4x}{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{4x^5-16x^3-24x^3+96x - \left(4x^5-48x^3\right) }{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{4x^5-16x^3-24x^3+96x - 4x^5+48x^3 }{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{8x^3+96x }{\left(x^2-4\right)^3 }$

Ora calcoliamo le radici della derivata seconda della funzione:

$f''(x)= 0$

$\cfrac{8x^3+96x }{\left(x^2-4\right)^3 }=0$

Il termine

$\left(x^2-4\right)^3$

Ciò comporta la divisione dell’intero lato sinistro, quindi possiamo moltiplicarlo per l’intero lato destro:

$8x^3+96x =0\cdot \left(x^2-4\right)^3$

$8x^3+96x =0$

Estraiamo il fattore comune:

$x(8x^2+96)=0$

Perché la moltiplicazione sia uguale a 0, uno dei due elementi della moltiplicazione deve essere zero. Pertanto, impostiamo ciascun fattore uguale a 0:

$\displaystyle x\cdot(8x^2+96) =0 \longrightarrow \begin{cases} \bm{x =0} \\[2ex] 8x^2+96=0 \ \longrightarrow \ x^2=\cfrac{-96}{8}} = -12 \ \longrightarrow \ x= \sqrt{-12} \ \color{red}\bm{\times} \end{cases}$

$x= \sqrt{-12}$

Non esiste una soluzione poiché non esiste una radice negativa di un numero reale.

Rappresentiamo ora sulla retta tutti i punti critici ottenuti, cioè i punti che non appartengono al dominio (x=-2 e x=+2) e quelli che annullano la derivata seconda (x=0):

E valutiamo il segno della derivata seconda in ogni intervallo, per sapere se la funzione è concava o convessa. Quindi prendiamo un punto in ogni intervallo e guardiamo quale segno ha la derivata seconda in quel punto:

$f''(-3)=\cfrac{8(-3)^3+96(-3) }{\left((-3)^2-4\right)^3 } = \cfrac{-504}{125}=-4,03 \ \rightarrow \ \bm{-}$

$f''(-1)=\cfrac{8(-1)^3+96(-1) }{\left((-1)^2-4\right)^3 } = \cfrac{-104}{-27}=3,85 \ \rightarrow \ \bm{+}$

$f''(1)=\cfrac{8\cdot1^3+96\cdot 1 }{\left(1^2-4\right)^3 } = \cfrac{104}{-27}=-3,85 \ \rightarrow \ \bm{-}$

$f''(3)=\cfrac{8\cdot 3^3+96\cdot 3 }{\left(3^2-4\right)^3 } = \cfrac{504}{125}=4,03 \ \rightarrow \ \bm{+}$

Se la derivata seconda è positiva significa che la funzione è convessa.

$(\bm{\cup})$

, e se la derivata seconda è negativa significa che la funzione è concava

$(\bm{\cap})$

. Gli intervalli di concavità e convessità sono quindi:

Convesso

$(\bm{\cup})$

$\bm{(-2,0)\cup (2,+\infty)}$

Concavo

$(\bm{\cap})$

$\bm{(-\infty,-2)\cup (0,2)}$

Esercizio 3

Una funzione

$f(x)$

ha un estremo relativo in

$x=3$

. Inoltre la funzione è convessa

$(\cup )$

in questo stesso punto. Determina se l’estremo relativo è un minimo o un massimo.

➤ Vedi: definizione di massimi e minimi di una funzione

Vedi la soluzione

Lascia che la funzione convessa

$(\cup)$

$x=3$

significa che la derivata seconda a questo punto è positiva, cioè

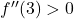$f''(3)>0″ title=”Rendered by QuickLaTeX.com” height=”19″ width=”74″ style=”vertical-align: -5px;”></p> <p> .</p> <p class=$ Pertanto, l’estremo relativo di

$\bm{x=3}$

Questo è il minimo , da allora

$f''(3)$

È positivo.

Che cosa sono la concavità e la convessità di una funzione?

Come studiare la curvatura di una funzione

Esempio di come trovare la curvatura di una funzione

Esercizi risolti sulla concavità e convessità di una funzione

Esercizio 1

Esercizio 2

Esercizio 3

Lascia un commento Annulla risposta