Funzione costante - Mathority

In questo articolo spieghiamo cos’è una funzione costante e qual è la sua rappresentazione grafica. Inoltre potrai vedere diversi esempi di funzioni costanti e tutte le caratteristiche di questo tipo di funzioni. E, infine, potrai allenarti con esercizi risolti a funzioni costanti.

Cos’è una funzione costante?

Una funzione costante è quella funzione che assume sempre la stessa immagine per qualsiasi valore della variabile indipendente (x) , ovvero una funzione costante è della forma f(x)=k , dove k è un numero reale qualsiasi.

$f(x)=k$

La rappresentazione grafica di una funzione costante è una linea orizzontale.

Ad esempio, tutte le seguenti funzioni sono costanti:

$f(x)=1 \qquad f(x)=7 \qquad f(x)=5$

Rappresentazione grafica di una funzione costante

Una volta visto il concetto di funzione costante, vedremo come rappresentare una funzione costante in un grafico.

Rappresentare graficamente una funzione costante è abbastanza semplice, basta tracciare una linea orizzontale nel valore della funzione (k).

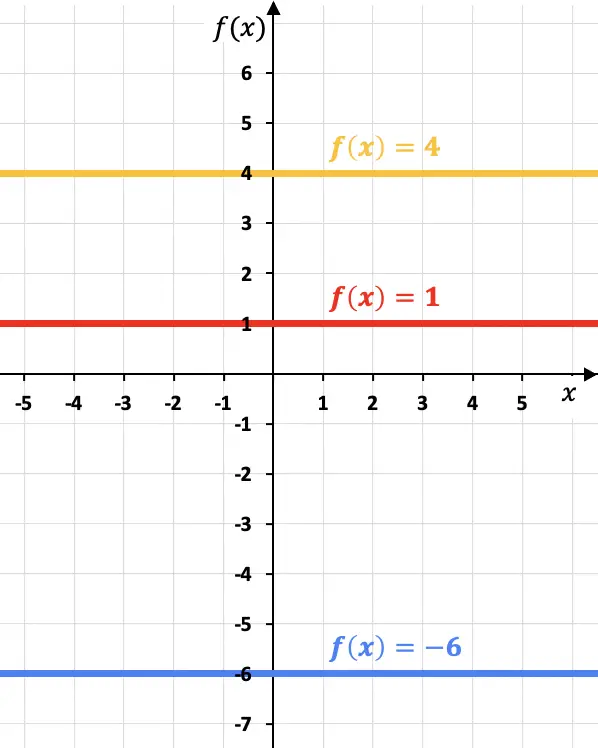
Guarda i seguenti esempi in cui abbiamo rappresentato tre diverse funzioni costanti su un grafico:

Nota che ogni funzione costante è parallela all’asse x.

D’altra parte, devi tenere presente che una linea verticale non è una funzione costante. In effetti, una linea verticale non è nemmeno una funzione, poiché per definizione una funzione può avere solo un’immagine per ogni valore di x.

Caratteristiche della funzione costante

Successivamente analizzeremo le proprietà della funzione costante. Consideriamo una funzione costante di qualsiasi valore:

$f(x)=k$

Il dominio della funzione costante è costituito da tutti i numeri reali:

$\text{Dom } f = \mathbb{R}$

Il percorso o l’intervallo della funzione costante è solo il valore della costante:

$\text{Im } f= k$

È una funzione continua e pari, perché la funzione assume sempre lo stesso valore:

$\displaystyle f(x)=f(-x)$

La funzione costante non è né crescente né decrescente, è un tipo di funzione che ha sempre pendenza zero:

$m=0$

Interseca sempre l’asse OY nel punto (0,k).

$(0,k)$

Ogni funzione costante è un polinomio di grado zero.

Sì
$k\neq 0$

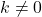
la funzione costante non ha radice, invece, se

$k=0$

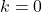
tutti i numeri reali sono le radici della funzione costante.

Il limite della funzione costante quando x si avvicina a più infinito o meno infinito è uguale al valore della costante:

$\displaystyle\lim_{x\to +\infty} f(x)=k$

$\displaystyle\lim_{x\to -\infty} f(x)=k$

La derivata della funzione costante è sempre zero:

$f(x)=k \ \longrightarrow \ f'(x)=0$

In effetti, la definizione di funzione costante può essere fatta anche a partire dalla nozione di derivata: una funzione è costante se la sua derivata si annulla in tutto il suo dominio.

L’integrale della funzione costante è la funzione lineare (o affine):

$\displaystyle \int k \ dx= x + C$

➤ Vedi: Cos’è una funzione lineare?

Funzione costante su un intervallo

Abbiamo visto come una funzione sia costante, tuttavia una funzione può essere costante solo in un intervallo del suo dominio.

Per comprendere questo concetto è necessario sapere quali funzioni sono definite in blocchi, quindi prima di continuare ti consigliamo di dare un’occhiata alla seguente spiegazione:

➤ Vedi: Cos’è una funzione a tratti?

Una volta che sai quali sono questi tipi di funzioni, guarda la funzione definita nelle parti mostrate di seguito:

Come puoi vedere dal grafico, la funzione non è costante su tutti i numeri nel suo dominio. Ma è costante nell’intervallo [-2,4), quindi è una funzione costante solo in un intervallo.