Funzione coseno iperbolico

Qui troverai tutto sulla funzione coseno iperbolico: qual è la sua formula, la sua rappresentazione grafica, le sue caratteristiche, le relazioni matematiche con le altre funzioni, ecc.

Formula del coseno iperbolico

La funzione coseno iperbolico è una delle principali funzioni iperboliche ed è rappresentata dal simbolo cosh(x) . Il coseno iperbolico è uguale alla somma di e ^x più e ^-x divisa per 2.

Pertanto la formula del coseno iperbolico è:

$\displaystyle\text{cosh}(x)=\cfrac{e^{x}+e^{-x}}{2}$

Pertanto, il coseno iperbolico è matematicamente correlato alla funzione esponenziale. Nel seguente link potete vedere le proprietà di questo tipo di funzione:

➤ Vedi:proprietà della funzione esponenziale

Rappresentazione grafica del coseno iperbolico

La rappresentazione grafica della funzione coseno iperbolico è sotto forma di funzione quadratica (o parabola):

➤ Vedi: Rappresentazione grafica di una funzione quadratica .

In questo grafico possiamo vedere chiaramente che il coseno iperbolico è una funzione pari, perché è simmetrica rispetto all’asse y.

D’altro canto il grafico del coseno iperbolico è molto diverso da quello del coseno (funzione trigonometrica), che è una funzione periodica. Puoi vedere la rappresentazione grafica del coseno e tutte le differenze con il coseno iperbolico nel seguente link:

➤ Vedi: rappresentazione grafica della funzione coseno

Caratteristiche del coseno iperbolico

Il coseno iperbolico rispetta le seguenti proprietà:

Il dominio della funzione coseno iperbolico è composto da tutti i numeri reali:

$\text{Dom } f = \mathbb{R}$

Invece, l’intervallo (o intervallo) della funzione coseno iperbolico è 1 e tutti i numeri maggiori di 1:

$\text{Im } f= [1,+\infty)$

Il coseno iperbolico è una funzione continua e pari.

$\displaystyle \text{cosh}(-x)=\text{cosh}(x)$

La funzione interseca l’asse Y nel punto x=0.

$(0,1)$

D’altra parte la funzione non ha punto di intersezione con l’asse X.

I due limiti all’infinito (positivo e negativo) della funzione coseno iperbolico danno più infinito.

$\displaystyle\lim_{x\to+\infty}\text{cosh}(x)=+\infty$

$\displaystyle\lim_{x\to-\infty}\text{cosh}(x)=+\infty$

Il coseno iperbolico diminuisce fino a x = 0 e da quel punto aumenta indefinitamente, quindi la funzione ha un minimo in x = 0.

$(0,1)$

La funzione è convessa in tutto il suo dominio, quindi non ha punti di flesso.

La derivata della funzione coseno iperbolico è il seno iperbolico:

$f(x)=\text{cosh}(x) \ \longrightarrow \ f'(x)=\text{senh}(x)$

L’integrale della funzione coseno iperbolico è il seno iperbolico:

$\displaystyle \int \text{cosh}(x) \ dx= \text{senh}(x) + C$

Il polinomio di Taylor (o serie di Maclaurin) della funzione coseno iperbolico è il seguente:

$\displaystyle\text{cosh}(x)=1+\cfrac{x^2}{2!}+\cfrac{x^4}{4!}+\cfrac{x^6}{6!}+\dots=\sum_{n=0}^\infty\cfrac{x^{2n}}{(2n)!}$

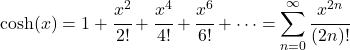
La trasformata di Laplace della funzione coseno iperbolico è la seguente:

$\mathcal{L}\bigl[\text{cosh}(at)\bigr]=\cfrac{s}{s^2-a^2}$

Relazioni matematiche del coseno iperbolico

Successivamente vedremo come il coseno iperbolico può essere calcolato da altre funzioni iperboliche, poiché sono tutte matematicamente correlate.

L’equazione fondamentale mette in relazione il coseno iperbolico con il seno iperbolico:

$\text{cosh}^2(x)-\text{senh}^2(x)=1$

➤ Vedi: seno iperbolico

Le tre principali funzioni iperboliche (seno iperbolico, coseno e tangente) possono essere correlate dalla seguente equazione:

$\text{tanh}(x)=\cfrac{\text{senh}(x)}{\text{cosh}(x)}$

D’altra parte, il coseno iperbolico della somma (o sottrazione) di due numeri diversi può essere determinato mediante le seguenti formule:

$\text{cosh}(x+y)=\text{cosh}(x)\text{cosh}(y)+\text{senh}(y)\text{senh}(x)$

$\text{cosh}(x-y)=\text{cosh}(x)\text{cosh}(y)-\text{senh}(y)\text{senh}(x)$

Il coseno iperbolico di due volte un numero è uguale alla somma dei quadrati del coseno iperbolico e del seno iperbolico di questo numero:

$\text{cosh}(2x)=\text{cosh}^2(x)+\text{senh}^2(x)$

L’addizione o la sottrazione di due coseni iperbolici può essere calcolata applicando le seguenti formule:

$\displaystyle\text{cosh}(x)+\text{cosh}(y)=2\text{cosh}\left(\frac{x+y}{2}\right)\text{cosh}\left(\frac{x-y}{2}\right)$

$\displaystyle\text{cosh}(x)-\text{cosh}(y)=2\text{senh}\left(\frac{x+y}{2}\right)\text{senh}\left(\frac{x-y}{2}\right)$

Infine, il quadrato del coseno iperbolico può essere calcolato con la seguente formula:

$\text{cosh}^2(x)=\cfrac{1}{2}\Bigl(\text{cosh}(2x)+1\Bigr)$

Formula del coseno iperbolico

Rappresentazione grafica del coseno iperbolico

Caratteristiche del coseno iperbolico

Relazioni matematiche del coseno iperbolico

Lascia un commento Annulla risposta