▷ Come sapere se una funzione è continua (esercizi risolti)

In questo articolo spieghiamo cosa sono le funzioni continue e come determinare se una funzione è continua in un punto oppure no. Inoltre, troverai le proprietà delle funzioni continue e l’analisi di continuità delle funzioni più comuni. Infine, puoi esercitarti con esercizi risolti sulla funzione continua per comprendere appieno il concetto.

Cos’è una funzione continua?

La continuità di una funzione può essere studiata graficamente. Una funzione continua è una funzione che può essere rappresentata su un grafico senza togliere la matita dal foglio.

Funzione continua

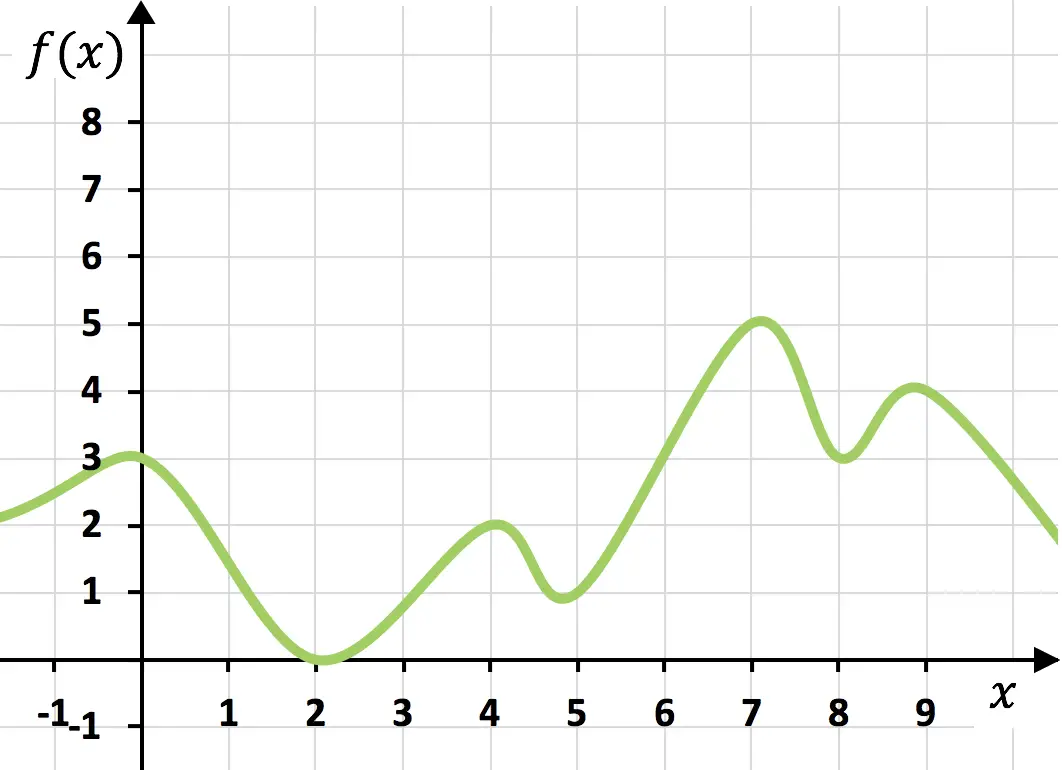
La funzione di cui sopra è continua perché può essere disegnata in un colpo solo senza staccare la mano dal foglio.

D’altra parte, quando la precedente condizione di continuità non è inserita in una funzione, si dice che sia una funzione discontinua .

Funzione discontinua

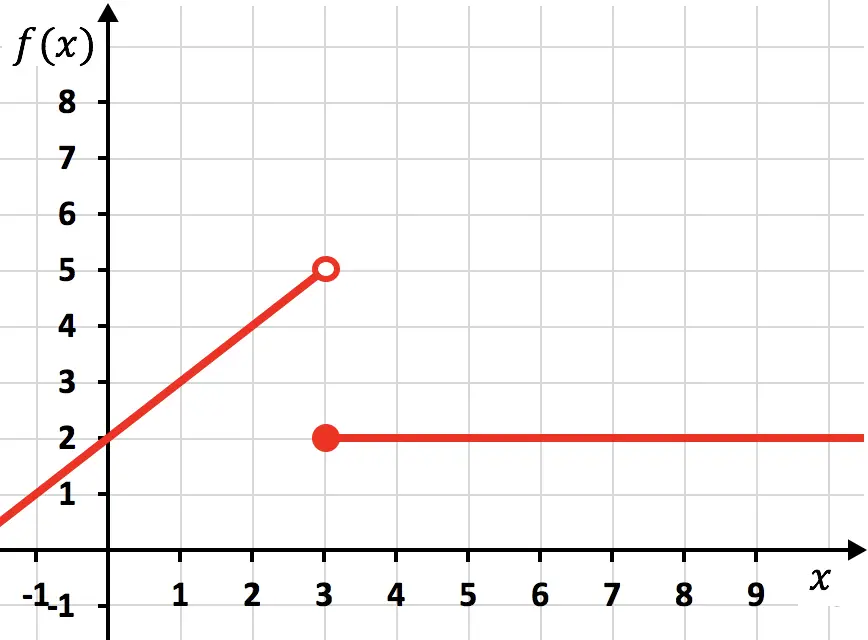
La funzione precedente è discontinua perché per rappresentarla bisogna tracciare due linee con la matita. In questo caso la funzione cessa di essere continua in x=3, diciamo quindi che x=3 è un punto di discontinuità .

Inoltre, ci sono tre tipi di discontinuità : discontinuità evitabile, discontinuità inevitabile a salti finiti e discontinuità inevitabile a salti infiniti. Nel seguente collegamento puoi vedere come appare ogni tipo di discontinuità e cosa c’è di diverso in ciascuno di essi:

➤ Vedi: tipi di discontinuità

Continuità di una funzione in un punto

Una volta visto come appare il grafico di una funzione continua, vedremo come determinare analiticamente se una funzione è continua o meno.

Matematicamente una funzione è continua in un punto se sono soddisfatte le seguenti tre condizioni:

La funzione esiste in questo punto, cioè esiste l’immagine del punto.

$\exists \ f(a)$

C’è il limite della funzione a questo punto. Pertanto, i limiti laterali sinistro e destro della funzione in questo punto sono uguali.

$\displaystyle \lim_{x \to a^-} f(x) = \lim_{x \to a^+} f(x) \quad \color{orange}\bm{\longrightarrow}\color{black} \quad \exists \lim_{x \to a} f(x)$

L’immagine del punto coincide in questo punto con il limite della funzione.

$\displaystyle f(a)=\lim_{x \to a} f(x)$

Pertanto, se le tre condizioni di continuità sono soddisfatte in tutti i punti di una funzione, la funzione è continua.

Ad esempio, analizzeremo la continuità della seguente funzione a tratti:

continuità di una funzione definita a tratti

Anche se cambi sezione, al punto

$x=-2$

La funzione è continua, poiché i limiti laterali della funzione in questo punto sono uguali e coincidono maggiormente con il valore della funzione in questo punto.

$\lim\limits_{x \to -2^-} f(x)=\lim\limits_{x \to -2^+} f(x)= f(-2)=3$

D’altra parte la funzione non è continua in quel punto

$x=4$

perché i due limiti laterali sono diversi e quindi il limite della funzione a questo punto non esiste:

$\lim\limits_{x \to 4^-} f(x)=3 \neq \lim\limits_{x \to 4^+} f(x)= 2$

In breve, la funzione definita dai pezzi è continua in tutti i numeri reali tranne che in

$x=4,$

dove c’è una discontinuità.

Possiamo anche verificare che la funzione è discontinua in

$x=4$

perché per rappresentarlo graficamente è necessario staccare a questo punto la matita dal foglio.

Continuità delle funzioni elementari

Alcuni tipi di funzioni sono continue per le loro caratteristiche:

Le funzioni costanti sono continue in tutti i numeri reali.

$f(x)=k$

Le funzioni polinomiali sono continue per tutti i numeri reali.

$f(x)=a_0+a_1x+a_2x^2+a_3x^3+\dots+a_nx^n$

Le funzioni razionali (o frazionarie) sono continue in tutti i numeri reali tranne nei valori che annullano il denominatore della frazione, in questi punti la funzione presenta una discontinuità.

$f(x)=\cfrac{p(x)}{q(x)}$

Le funzioni esponenziali sono continue su tutti i numeri reali:

$f(x)=a^x$

Le funzioni logaritmiche sono continue in tutti i punti che rendono positivo il loro argomento.

$f(x)=\log_a (x)$

La continuità delle funzioni irrazionali , o funzioni con radici, dipende dall’indice del radicale (n). Se l’indice è pari, si tratta di funzioni continue in tutti i punti che rendono l’argomento radice uguale o maggiore di zero. Ma se l’indice è dispari, si tratta di funzioni continue su tutti i numeri reali.

$f(x)=\sqrt[n]{x}$

La continuità delle funzioni trigonometriche dipende dal tipo di funzione. La funzione seno e la funzione coseno sono continue sull’insieme dei numeri reali, ma la funzione tangente è discontinua nei punti
$\displaystyle x=\frac{\pi}{2}+k\pi$

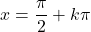
(dove k è un numero intero).

$f(x)=sen(x)\qquad f(x)=cos(x)\qquad f(x)=tg(x)$

Proprietà delle funzioni continue

Sean

$f(x)$

$g(x)$

due funzioni continue nel punto

$x=a,$

Prossimo:

La somma di due funzioni continue in un punto è un’altra funzione continua in quel punto.

$f(x)+g(x)$

Il prodotto di due funzioni continue in un punto è uguale a un’altra funzione continua in quel punto.

$f(x)\cdot g(x)$

Dividendo due funzioni continue in un punto si ottiene un’altra funzione continua in quel punto, purché quel punto non annulli la funzione di divisione.

$\cfrac{f(x)}{g(x)}\qquad g(a)\neq 0$

La composizione di due funzioni continue in un punto dà origine ad una funzione continua in quello stesso punto.

$f(x)\circ g(x)$

➤ Vedi: cos’è una funzione composta?

Esercizi risolti sulla continuità di una funzione

Esercizio 1

Trova le discontinuità della funzione mostrata nel grafico seguente. Determinare anche di che tipo di discontinuità si tratta.

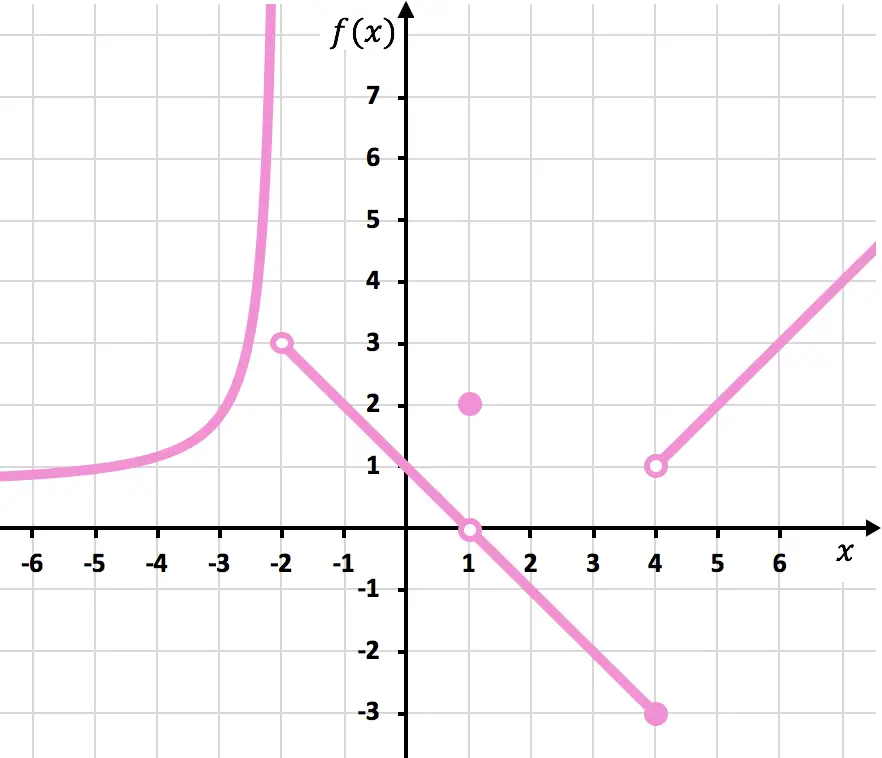
l'esercizio risolveva le discontinuità delle funzioni

Nota: per svolgere questo esercizio ti consigliamo di vedere prima quali sono i diversi tipi di discontinuità e come vengono identificate. Puoi vedere la spiegazione nel collegamento al principio dei tipi di discontinuità .

Vedi la soluzione

Per disegnare la funzione devi alzare la matita in x=-2, in x=1 e in x=4. La funzione è quindi discontinua in questi tre punti.

In x=-2, il limite del lato sinistro è +∞ e il limite del lato destro è 3. Pertanto, poiché uno dei limiti laterali è infinito, la funzione ha un’inevitabile discontinuità di salto infinito in x=-2.

$\displaystyle \lim_{x \to -2^-} f(x) = +\infty \ \neq \ \lim_{x \to -2^+} f(x) = 3$

Il limite della funzione in x=1 è 0 e, invece, il valore della funzione in x=1 è uguale a 2. La funzione presenta quindi una discontinuità evitabile in x=1.

$\displaystyle \lim_{x \to 1^-} f(x) = \lim_{x \to 1^+} f(x) = 0 \ \bm{\longrightarrow} \ \lim_{x \to 1} f(x) = 0$

$\displaystyle \lim_{x \to 1} f(x) = 0 \neq f(0) = 2$

In x = 4, il limite del lato sinistro è -3 e il limite del lato destro è 1. Pertanto, poiché i due limiti laterali sono diversi e nessuno dei due dà infinito, la funzione ha inevitabilmente una discontinuità di salto finito in x =4.

$\displaystyle \lim_{x \to 4^-} f(x) = -3 \ \neq \ \lim_{x \to 4^+} f(x) = 1$

Esercizio 2

Determina i punti in cui la funzione mostrata nel grafico seguente è discontinua.

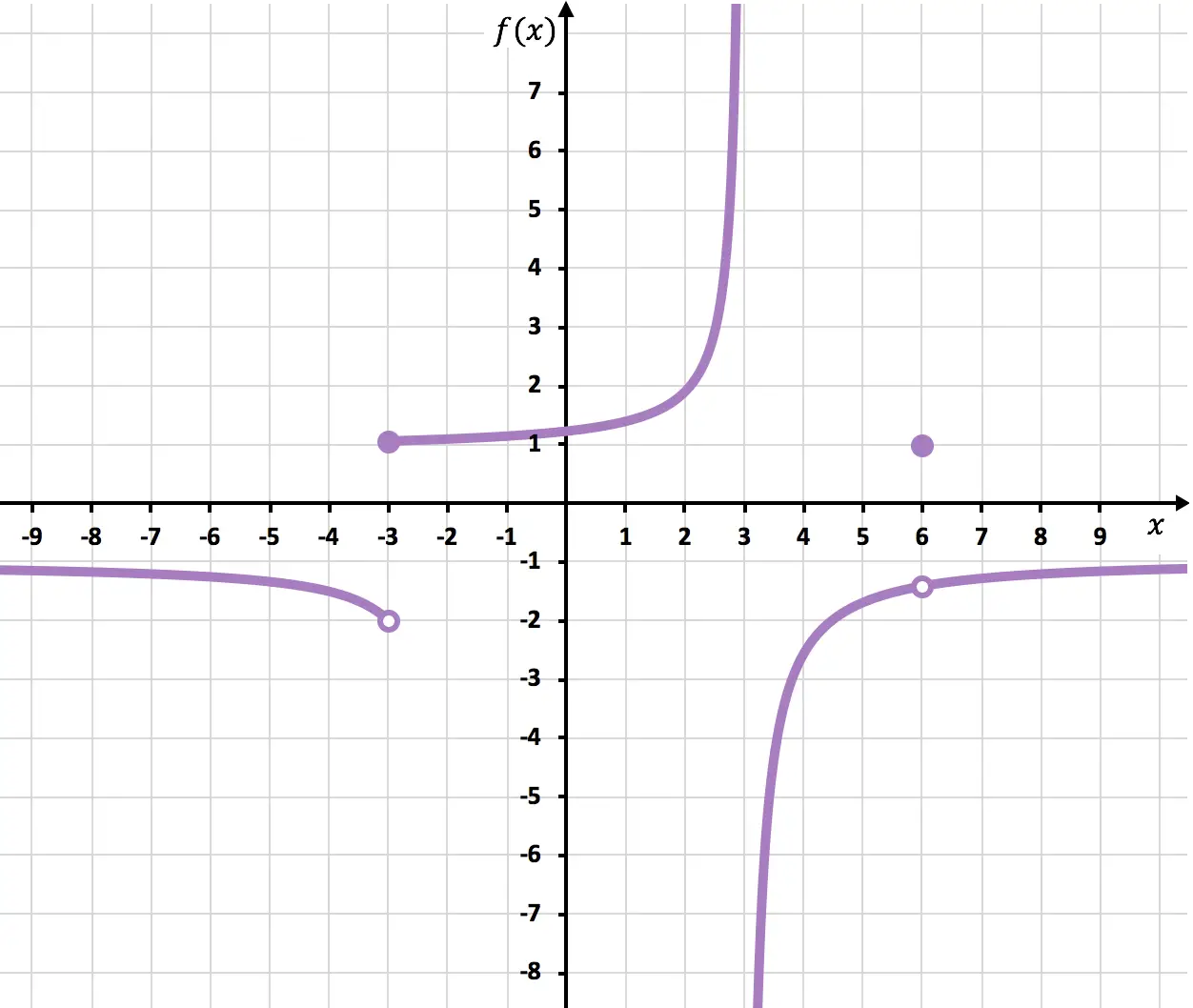
esercizio risolto sui tipi di discontinuità di una funzione

Vedi la soluzione

Nel punto x=6 la funzione viene interrotta perché c’è un punto in sospeso. Il limite quando x si avvicina a 6 è -1,4 ma f(6)=1. La funzione presenta quindi una discontinuità evitabile in x=6 perché il valore del limite non coincide con il valore della funzione:

$\displaystyle \left. \begin{array}{l} \displaystyle \lim_{x \to 6^-} f(x)=-1,4\\[3ex] \displaystyle \lim_{x \to 6^+} f(x)=-1,4 \end{array} \right\} \bm{\longrightarrow} \lim_{x \to 6} f(x)=-1,4$

$\displaystyle\lim_{x \to 6} f(x)=-1,4 \neq f(6)=1$

A x=-3 i limiti laterali non coincidono e nessuno dà infinito. La funzione presenta quindi un’inevitabile discontinuità di salto finito in x=-3.

$\displaystyle \lim_{x \to -3^-} f(x)=-2 \neq \lim_{x \to -3^+} f(x)=1$

E infine, la funzione ha un’inevitabile discontinuità di salto infinito in x = 3, poiché almeno un limite laterale a questo punto risulta in infinito.

$\displaystyle \lim_{x \to 3^-} f(x)=+\infty \qquad \lim_{x \to 3^+} f(x)=-\infty$

Esercizio 3

Analizzare la continuità della seguente funzione razionale:

$\displaystyle f(x)= \frac{2}{x-5}$

Vedi la soluzione

Le funzioni razionali sono continue in tutto il loro dominio, cioè in tutti i numeri reali tranne i valori che annullano il denominatore. Pertanto, poniamo il denominatore della funzione razionale uguale a zero per vedere quali punti non appartengono al dominio:

$x-5=0$

$x=5$

$\text{Dom } f = \mathbb{R} - \{5\}$

La funzione sarà quindi continua in tutti i punti tranne x=5.

Esercizio 4

Analizzare la continuità della seguente funzione a tratti:

$\displaystyle f(x)= \left\{ \begin{array}{lcl} 5x-2 & \text{si} & x < 1 \\[2ex] x^2+2 & \text{si} & x \geq 1 \end{array} \right.$

Vedi la soluzione

La funzione è continua anche nella prima sezione,

$5x-2$

, come nella seconda sezione,

$x^2+2$

, poiché sono funzioni polinomiali.

Quindi l’unico punto in cui la funzione potrebbe essere discontinua è il punto in cui la funzione si interrompe a pezzi. Calcoliamo quindi a questo punto i limiti laterali:

$\displaystyle \lim_{x \to 1^-} f(x) = \lim_{x \to 1} (5x-2)=5\cdot 1-2=\bm{3}$

$\displaystyle \lim_{x \to 1^+} f(x) = \lim_{x \to 1} (x^2+2)=1^2+2=\bm{3}$

I due limiti laterali coincidono quindi, il limite della funzione quando x tende a 1 è pari a 3:

$\displaystyle \lim_{x \to 1^-} f(x) = \lim_{x \to 1^+} f(x) = 3 \ \bm{\longrightarrow} \ \exists \lim_{x \to 1} f(x) = 3$

Inoltre, anche l’immagine di x=1 è 3:

$f(1)=1^2+2=\bm{3}$

Pertanto, poiché il limite della funzione in x=1 è uguale all’immagine di detto punto, la funzione è continua nel punto x=1. E quindi è continua in tutti i numeri reali.

$\displaystyle f(1)=\lim_{x \to 1} f(x)$

Esercizio 5

Studia la continuità della seguente funzione irrazionale:

$f(x)=\sqrt{2x+6}$

Vedi la soluzione

È una funzione radicale con indice pari, quindi la funzione sarà continua finché l’argomento del radicale è maggiore di 0 (perché la radice quadrata di un numero negativo non esiste):

$2x+6\ge 0$

Risolviamo la disuguaglianza:

$2x\ge -6$

$x\ge \cfrac{-6}{2}$

$x\ge -3$

La soluzione è composta da tutti i numeri maggiori o uguali a -3. La funzione è quindi continua sull’intervallo del suo dominio:

$\mathbf{Dom } \ \bm{f = [-3,+\infty) }$

Esercizio 6

Analizzare la continuità della seguente funzione logaritmica:

$f(x)=\log_3 (-3x+6)$

Vedi la soluzione

Questa è una funzione logaritmica e non esiste né il logaritmo di un numero negativo né il logaritmo di 0. Pertanto, la funzione esisterà finché l’argomento del logaritmo sarà positivo (maggiore di zero):

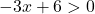$-3x+6>0″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”95″ style=”vertical-align: -2px;”> <p class=$ Risolviamo la disuguaglianza:

$-3x>-6″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”78″ style=”vertical-align: -2px;”> <p class=$ $x<\cfrac{-6}{-3}$

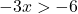
Ricorda che quando dividi un numero negativo per l’altro lato di una disuguaglianza, devi invertire il segno della disuguaglianza.

$x<2$

La soluzione è costituita da tutti i numeri minori di 2. Il dominio di definizione della funzione è quindi:

$\mathbf{Dom } \ \bm{f = (-\infty,2) }$

La funzione è quindi continua in ogni punto del suo dominio.

Esercizio 7

Calcolare la continuità della seguente funzione:

$f(x)=\cfrac{4x-2}{\sqrt{-2x-8}}$

Vedi la soluzione

Al denominatore della frazione abbiamo un radicale con indice pari, quindi la funzione esisterà ogni volta che il contenuto della radice sarà uguale o maggiore di zero:

$-2x-8\geq 0$

Inoltre, la radice è nel denominatore della frazione e il denominatore di una frazione non può mai essere 0. Quindi la funzione esisterà solo se il contenuto della radice è strettamente maggiore di 0:

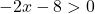$-2x-8> 0″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”95″ style=”vertical-align: -2px;”> <p class=$ Ora risolviamo la disuguaglianza:

$-2x>8″ title=”Rendered by QuickLaTeX.com” height=”14″ width=”64″ style=”vertical-align: -2px;”> <p class=$ $x<\cfrac{8}{-2}$

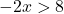
Ricorda che quando cambiamo i lati di un numero negativo moltiplicando o dividendo una disuguaglianza, dobbiamo anche ruotare il segno della disuguaglianza.

$x<-4$

Il risultato sono tutti i numeri inferiori a -4. Pertanto il dominio della funzione, e quindi la sua continuità, sono definiti dal seguente intervallo:

$\mathbf{Dom } \ \bm{f = (-\infty,-4) }$

Esercizio 8

Calcolare il valore di k in modo che la funzione sia continua ovunque

$\mathbb{R} .$

$\displaystyle f(x)= \left\{ \begin{array}{lcl} kx-1 & \text{si} & x \leq 2 \\[2ex] 3x^2 - 5 & \text{si} & x > 2 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”65″ width=”225″ style=”vertical-align: 0px;”> <div class=$

Vedi la soluzione

Affinché la funzione sia continua, i due limiti laterali nel punto di interruzione devono dare lo stesso risultato. Calcoliamo quindi prima il limite laterale al punto di rottura della parte che non ha k :

$\displaystyle \lim_{x \to 2^+} f(x) = \lim_{x \to 2} (3x^2 - 5) = 3\cdot 2^2-5=\bm{7}$

Pertanto, affinché la funzione a tratti sia continua, anche il limite dell’altro lato deve essere uguale a 7.

$\displaystyle \lim_{x \to 2^-} f(x) = \lim_{x \to 2} (kx-1) = k\cdot2 -1= 2k-1$

Pertanto, affinché la funzione sia continua, i due limiti laterali di un punto qualsiasi devono dare lo stesso risultato. Poniamo quindi l’espressione ottenuta dal limite pari a 7 (il risultato dell’altro limite laterale).