Frazioni algebriche: semplificazione, operazioni, esercizi risolti, ecc. -

In questa pagina spieghiamo cosa sono le frazioni algebriche, quando sono equivalenti, come semplificarle e come eseguire operazioni con le frazioni algebriche (addizione, sottrazione, moltiplicazione e divisione). Inoltre, potrai vedere esercizi passo passo risolti per le frazioni algebriche. In breve, qui troverai tutto sulle frazioni algebriche.

Cosa sono le frazioni algebriche?

In matematica una frazione algebrica è una frazione che ha un polinomio al numeratore e un altro polinomio al denominatore.

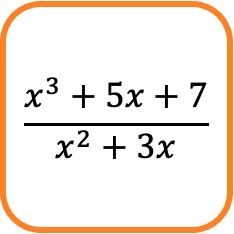
Ad esempio, l’espressione frazionaria sopra è costituita da una frazione algebrica perché il suo numeratore e denominatore sono costituiti da polinomi.

Frazione algebrica equivalente

Una volta che conosciamo la definizione di frazioni algebriche, vediamo quando due di queste frazioni sono uguali.

Matematicamente, due frazioni algebriche sono equivalenti se è soddisfatta la seguente condizione:

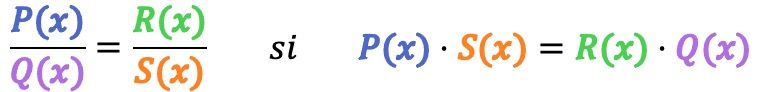
Ad esempio, controlleremo se le seguenti 2 frazioni algebriche sono equivalenti:

$\cfrac{x+3}{x^2+5x+6} \qquad \cfrac{1}{x+2}$

Per determinare se le frazioni sono algebricamente uguali, moltiplichiamo trasversalmente i loro termini:

$(x+3)\cdot (x+2) = (x^2+5x+6)\cdot 1$

Ora calcoliamo le moltiplicazioni dei polinomi:

$x^2+2x+3x+6 = x^2+5x+6$

$x^2+5x+6 = x^2+5x+6$

Abbiamo la stessa espressione su entrambi i lati dell’equazione, quindi sono effettivamente due frazioni algebriche equivalenti.

Semplificare le frazioni algebriche

Per semplificare una frazione algebrica, devi prima fattorizzare i polinomi del numeratore e del denominatore, quindi eliminare i fattori che hanno in comune.

Ovviamente, per semplificare le frazioni algebriche, è essenziale sapere cos’è la fattorizzazione polinomiale e come si fa. Se ancora non sai come si scompongono i polinomi o non lo ricordi completamente, ti consiglio di andare alla pagina collegata prima di proseguire, altrimenti capirai a malapena la procedura. Spiega passo dopo passo come fattorizzare i polinomi e, inoltre, potrai vedere diversi esempi ed esercitarti con esercizi risolti.

Vediamo ora come si semplifica una frazione algebrica applicando il metodo della fattorizzazione dei polinomi utilizzando un esempio:

Semplifica la seguente frazione algebrica:

$\cfrac{x^3+2x^2-x-2}{x^2-2x+1}$

Per prima cosa fattorizziamo i polinomi del numeratore e del denominatore della frazione:

$\cfrac{(x-1)(x+1)(x+2)}{(x-1)(x-1)}$

⬆(Se non sai come sono stati scomposti i polinomi, dai un’occhiata al link qui sopra)⬆

E una volta scomposti i polinomi, eliminiamo i fattori comuni tra numeratore e denominatore, cioè togliamo tutti i termini che si ripetono:

$\cfrac{\cancel{(x-1)}(x+1)(x+2)}{\cancel{(x-1)}(x-1)}$

La frazione algebrica semplificata si presenta quindi così:

$\cfrac{(x+1)(x+2)}{x-1}$

In questo problema i polinomi della frazione algebrica sono stati scomposti trovando le loro radici; tuttavia, a volte un polinomio può essere scomposto direttamente utilizzando il fattore comune (metodo molto più veloce). In questo link vedrai cosa significa prendere un fattore comune da un polinomio e scoprirai come semplificare una frazione algebrica utilizzando un fattore comune.

Operazioni con le frazioni algebriche

Come ogni tipo di frazione, anche con le frazioni algebriche è possibile eseguire operazioni. Nello specifico, le frazioni algebriche possono essere aggiunte, sottratte, moltiplicate e divise. Di seguito spieghiamo passo passo con esempi come viene calcolata ogni tipologia di operazione.

Addizione e sottrazione di frazioni algebriche

La procedura per sommare e sottrarre le frazioni algebriche è praticamente identica, quindi le analizzeremo insieme. Per prima cosa vedremo un esempio di due frazioni algebriche aggiunte, e di seguito studieremo la differenza tra il metodo di sottrazione delle frazioni algebriche.

Somma di frazioni algebriche

L’addizione delle frazioni algebriche si esegue allo stesso modo delle frazioni normali: prima riduci le frazioni a un denominatore comune, quindi aggiungi i numeratori.

Vediamo come vengono aggiunte le frazioni algebriche utilizzando un esempio:

$\cfrac{x}{x^2+2x+1} + \cfrac{3x}{x^2+x}$

Per prima cosa fattorizziamo i denominatori delle frazioni:

$\cfrac{x}{(x+1)(x+1)} + \cfrac{3x}{x(x+1)}$

$\cfrac{x}{(x+1)^2} + \cfrac{3x}{x(x+1)}$

Ora dobbiamo trovare il cmm (minimo comune multiplo) dei denominatori per ridurre le frazioni a un denominatore comune.

Suggerimento: il mcm dei denominatori è sempre formato dal prodotto dei fattori che hanno in comune elevato all’esponente maggiore moltiplicato per i fattori non comuni .

Ad esempio, nel nostro caso

$\cfrac{x}{(x+1)^2} + \cfrac{3x}{x(x+1)}$

Il divisore comune tra i denominatori elevato al massimo esponente è

$(x+1)^2.$

E il fattore non comune tra i denominatori è

$x.$

Pertanto, il mcm dei denominatori in questo caso è:

$(x+1)^2 \cdot x$

Il mcm dei denominatori è quindi

$(x+1)^2 \cdot x,$

questo sarà quindi il nuovo denominatore delle 2 frazioni.

$\cfrac{x}{(x+1)^2} + \cfrac{3x}{x(x+1)} \ \longrightarrow \ \cfrac{}{x(x+1)^2} + \cfrac{}{x(x+1)^2}$

Una volta trovato il denominatore comune, dobbiamo modificare i numeratori. Per fare questo seguiamo lo stesso procedimento dell’addizione delle frazioni normali: per ogni frazione dividiamo i lcm

$\bigl( \ x(x+1)^2 \ \bigr)$

tra il denominatore originale e moltiplicare il risultato per il numeratore:

$\cfrac{x(x+1)^2}{(x+1)^2} = \cfrac{x\cancel{(x+1)^2}}{\cancel{(x+1)^2}} = \color{red}\bm{x}$

$\cfrac{x(x+1)^2}{x(x+1)}= \cfrac{\cancel{x}(x+1)^\cancel{2}}{\cancel{x}\cancel{(x+1)}}=\color{blue} \bm{x+1}$

$\cfrac{x}{(x+1)^2} + \cfrac{3x}{x(x+1)} \ \longrightarrow \ \cfrac{x \cdot \color{red}\bm{x} \color{black} }{x(x+1)^2} + \cfrac{3x \cdot \color{blue} \bm{(x+1)} \color{black}}{x(x+1)^2}$

Quindi ora possiamo mettere insieme le due frazioni perché hanno lo stesso denominatore:

$\cfrac{x^2+3x(x+1)}{x(x+1)^2}$

Infine operiamo sul numeratore. Per prima cosa calcoliamo il prodotto del monomio e del polinomio:

$\cfrac{x^2 +3x\cdot x+ 3x\cdot 1 }{x(x+1)^2}$

$\cfrac{x^2 +3x^2 + 3x }{x(x+1)^2}$

Successivamente, aggiungiamo i termini simili al numeratore:

$\cfrac{4x^2 + 3x }{x(x+1)^2}$

Normalmente ci saremmo già arrivati, ma se osserviamo da vicino il problema, possiamo semplificare ulteriormente la frazione algebrica rimuovendo un fattore comune dal numeratore. Ancora:

$\cfrac{x(4x + 3)}{x(x+1)^2}$

$\cfrac{\cancel{x}(4x + 3)}{\cancel{x}(x+1)^2}$

$\cfrac{4x + 3}{(x+1)^2}$

E così abbiamo già completato la somma delle due frazioni algebriche.

Sottrazione di frazioni algebriche

Per sottrarre le frazioni algebriche, dobbiamo seguire una procedura simile all’addizione delle frazioni algebriche: prima riduci le frazioni a un denominatore comune, quindi sottrai i numeratori.

Vediamo come si sottraggono le frazioni algebriche con un esempio:

$\cfrac{2x}{x^2-x-6} - \cfrac{4x-3}{(x+2)^2}$

Per prima cosa dobbiamo fattorizzare i denominatori delle due frazioni:

$\cfrac{2x}{(x+2)(x-3)} - \cfrac{4x-3}{(x+2)^2}$

Come per la sottrazione delle frazioni normali, ora dobbiamo calcolare il lcm (minimo comune multiplo) dei denominatori per ridurre le frazioni a un denominatore comune. In questo caso, il mcm dei denominatori è

$(x+2)^2(x-3) ,$

questo sarà quindi il nuovo denominatore delle 2 frazioni.

$\cfrac{2x}{(x+2)(x-3)} - \cfrac{4x-3}{(x+2)^2} \ \longrightarrow \ \cfrac{}{(x+2)^2(x-3)} + \cfrac{}{(x+2)^2(x-3)}$

Ora applichiamo lo stesso procedimento della sottrazione delle frazioni normali: per ogni frazione dividiamo i lcm

$\bigl( \ x(x+1)^2 \ \bigr)$

tra il denominatore originale e moltiplicare il risultato per il numeratore:

$\cfrac{(x+2)^2(x-3)}{(x+2)(x-3)} = \cfrac{(x+2)^{\cancel{2}}\cancel{(x-3)}}{\canel{(x+2)}\cancel{(x-3)}} = \color{red}\bm{x+2}$

$\cfrac{(x+2)^2(x-3)}{(x+2)^2}= \cfrac{\cancel{(x+2)^2}(x-3)}{\cancel{(x+2)^2}}=\color{blue} \bm{x-3}$

$\cfrac{2x}{(x+2)(x-3)} - \cfrac{4x-3}{(x+2)^2} \ \longrightarrow \ \cfrac{2x\cdot \color{red}\bm{(x+2)} \color{black}}{(x+2)^2(x-3)} + \cfrac{(4x-3)\cdot \color{blue} \bm{(x-3)} \color{black}}{(x+2)^2(x-3)}$

Uniamo ora le due frazioni algebriche poiché hanno lo stesso denominatore:

$\cfrac{2x(x+2)-(4x-3)(x-3)}{(x+2)^2(x-3)}$

E operiamo sul numeratore. Risolviamo innanzitutto le moltiplicazioni dei polinomi:

$\cfrac{2x^2+4x-\bigl[4x^2-12x-3x+9\bigr]}{(x+2)^2(x-3)}$

Un errore molto comune quando si sottraggono frazioni algebriche è dimenticare di mettere le parentesi dopo aver eseguito la moltiplicazione. Ciò sarebbe un errore poiché il segno negativo influisce su tutti gli elementi risultanti del prodotto, non solo sul primo termine.

Eseguiamo le operazioni tra parentesi:

$\cfrac{2x^2+4x-\bigl[4x^2-15x+9\bigr]}{(x+2)^2(x-3)}$

Quindi, grazie al segno negativo, cambiamo segno a tutti i termini tra parentesi:

$\cfrac{2x^2+4x-4x^2+15x-9}{(x+2)^2(x-3)}$

E, infine, raggruppiamo monomi simili:

$\cfrac{-2x^2+19x-9}{(x+2)^2(x-3)}$

Moltiplicazione di frazioni algebriche

Per moltiplicare le frazioni algebriche, prima fattorizziamo tutti i polinomi di dette frazioni, poi moltiplichiamo tra loro i numeratori e tra loro i denominatori e, infine, semplifichiamo la frazione ottenuta.

Pertanto, il prodotto delle frazioni algebriche viene effettivamente calcolato allo stesso modo del prodotto delle frazioni normali.

Successivamente, vediamo come moltiplicare due frazioni algebriche con un esempio:

$\cfrac{3x}{x^2+x-2} \cdot \cfrac{x^2-6x+5}{x+1}$

Innanzitutto devi fattorizzare tutti i polinomi delle frazioni, sia i numeratori che i denominatori:

$\cfrac{3x}{(x-1)(x+2)} \cdot \cfrac{(x-1)(x-5)}{x+1}$

Ora moltiplichiamo le frazioni. Per fare ciò, moltiplichiamo insieme numeratori e denominatori:

$\cfrac{3x \cdot (x-1)(x-5)}{(x-1)(x+2)\cdot (x+1)}$

$\cfrac{3x(x-1)(x-5)}{(x-1)(x+2)(x+1)}$

E infine semplifichiamo i fattori che si ripetono al denominatore e al numeratore:

$\cfrac{3x\cancel{(x-1)}(x-5)}{\cancel{(x-1)}(x+2)(x+1)}$

Il risultato della moltiplicazione è quindi:

$\cfrac{3x(x-5)}{(x+2)(x+1)}$

La frazione non può essere ulteriormente semplificata. Quindi abbiamo già finito di moltiplicare le frazioni algebriche.

Divisione delle frazioni algebriche

Per calcolare una divisione di frazioni algebriche , prima fattorizziamo tutti i polinomi, poi moltiplichiamo trasversalmente le frazioni (il primo numeratore per il secondo denominatore e il primo denominatore per il secondo numeratore) e infine semplifichiamo la frazione algebrica.

Vediamo allora meglio come si dividono due frazioni algebriche utilizzando un esempio:

$\cfrac{x^3-7x-6}{2x^2-8} : \cfrac{x^2+2x+1}{6}$

Il primo passo per dividere due frazioni algebriche è fattorizzare tutti i polinomi coinvolti nell’operazione:

$\cfrac{(x+1)(x+2)(x-3)}{2(x-2)(x+2)} : \cfrac{(x+1)^2}{6}$

Ora dobbiamo dividere le frazioni. Per fare questo moltiplichiamo le frazioni trasversalmente, cioè si moltiplica il primo numeratore per il secondo denominatore e il risultato sarà il numeratore della nuova frazione, e, allo stesso modo, si moltiplica il primo denominatore per il secondo numeratore e il risultato sarà il denominatore della nuova frazione:

$\cfrac{(x+1)(x+2)(x-3)\cdot 6}{2(x-2)(x+2)\cdot (x+1)^2}$

$\cfrac{6(x+1)(x+2)(x-3)}{2(x-2)(x+2)(x+1)^2}$

Semplifichiamo i fattori che si ripetono al denominatore e al numeratore:

$\cfrac{6\cancel{(x+1)}\cancel{(x+2)}(x-3)}{2(x-2)\cancel{(x+2)}(x+1)^\cancel{2}}$

$\cfrac{6(x-3)}{2(x-2)(x+1)}$

E possiamo semplificare ulteriormente la frazione, poiché

$6:2 = 3.$

$\cfrac{3(x-3)}{(x-2)(x+1)}$

La frazione non può essere ulteriormente semplificata. Pertanto, abbiamo già diviso le frazioni algebriche.

Esercizi risolti sulle frazioni algebriche

Di seguito ti proponiamo diversi esercizi risolti passo dopo passo sulle frazioni algebriche, in modo che tu possa esercitarti e finire così di comprendere il concetto. Non dimenticare che puoi farci tutte le domande che hai qui sotto nei commenti! 💬💬💬

Esercizio 1

Determina se le seguenti frazioni algebriche sono equivalenti o meno:

$\cfrac{x+3}{x^2-9} \qquad \cfrac{1}{x-3} \qquad \cfrac{x-3}{x^2+2x-3}$

Vedi la soluzione

Per verificare se due frazioni algebriche sono equivalenti, devi moltiplicarle trasversalmente e vedere se ottieni l’uguaglianza. Quindi controlleremo prima la prima e la seconda frazione:

$\cfrac{x+3}{x^2-9}= \cfrac{1}{x-3} \quad ?$

$(x+3)\cdot (x-3)=(x^2-9)\cdot 1$

Risolviamo l’identità notevole a sinistra dell’equazione:

$x^2-9=x^2-9$

✅

In questo caso abbiamo ottenuto un’uguaglianza, quindi la prima e la seconda frazione sono algebricamente uguali.

Applichiamo ora lo stesso procedimento con la prima e la terza frazione algebrica:

$\cfrac{x+3}{x^2-9}= \cfrac{x-3}{x^2+2x-3} \quad ?$

$(x+3)\cdot (x^2+2x-3)=(x^2-9)\cdot(x-3)$

$x^3+2x^2-3x+3x^2+6x-9=x^3-3x^2-9x+27$

$x^3+5x^2+3x-9=x^3-3x^2-9x+27$

❌

Tuttavia, questa volta le frazioni algebriche non soddisfano l’equazione, quindi la prima e la terza frazione sono matematicamente diverse.

In conclusione, la terza frazione è diversa dalla prima frazione e quindi è anche disuguale alla seconda frazione poiché la prima e la seconda frazione sono equivalenti.

$\cfrac{x+3}{x^2-9} = \cfrac{1}{x-3} \neq \cfrac{x-3}{x^2+2x-3}$

Esercizio 2

Semplifica le seguenti frazioni algebriche:

$\text{A)} \ \cfrac{5x^2+10x}{11x}$

$\text{B)} \ \cfrac{x^2-4}{x^2+2x-8}$

$\text{C)} \ \cfrac{x^3-2x^2-3x}{x^2-3x}$

$\text{D)} \ \cfrac{x^3-3x+2}{x^3+4x^2+x-6}$

Vedi la soluzione

Per semplificare una frazione algebrica, dobbiamo fattorizzare i polinomi del numeratore e del denominatore, quindi eliminare i fattori ripetuti. Ancora:

$\text{A)} \ \begin{array}{l} \cfrac{5x^2+10x}{11x} =\cfrac{5x(x+2)}{11x} = \\[4ex] =\cfrac{5\cancel{x}(x+2)}{11\cancel{x}}= \cfrac{\bm{5(x+2)}}{\bm{11}}\end{array}$

$\text{B)} \ \begin{array}{l} \cfrac{x^2-4}{x^2+2x-8} = \cfrac{(x-2)(x+2)}{(x-2)(x+4)}= \\[4ex] = \cfrac{\cancel{(x-2)}(x+2)}{\cancel{(x-2)}(x+4)}=\cfrac{\bm{x+2}}{\bm{x+4}}}\end{array}$

$\text{C)} \ \begin{array}{l} \cfrac{x^3-2x^2-3x}{x^2-3x} = \cfrac{x(x+1)(x-3)}{x(x-3)}}= \\[4ex] = \cfrac{\cancel{x} (x+1) \cancel{x-3}}{\cancel{x}\cancel{(x-3)}} = \cfrac{x+1}{1} = \\[4ex] = \bm{x+1}\end{array}$

$\text{D)} \ \begin{array}{l} \cfrac{x^3-3x+2}{x^3+4x^2+x-6}=\cfrac{(x-1)^2(x+2)}{(x-1)(x+3)(x+2)}= \\[4ex] = \cfrac{(x-1)^{\cancel{2}}\cancel{(x+2)}}{\cancel{(x-1)}(x+3)\cancel{(x+2)}}=\cfrac{\bm{x-1}}{\bm{x+3}}\end{array}$

Esercizio 3

Calcola le seguenti addizioni e sottrazioni di frazioni algebriche:

$\text{A)} \ \cfrac{4}{x^2+2x} + \cfrac{3x-2}{x^2-x-6}$

$\text{B)} \ \cfrac{4x}{x^3+2x^2+x} - \cfrac{2}{x^2-3x-4}$

$\text{C)} \ \cfrac{7x}{x^2-4x+4} + \cfrac{-5}{x-2}$

$\text{D)} \ x +\cfrac{-3x}{x^2-4} - \cfrac{2x^3-1}{2x^2+6x+4}$

Vedi la soluzione

Per aggiungere (o sottrarre) frazioni algebriche, dobbiamo prima ridurre le frazioni a un denominatore comune, quindi aggiungere (o sottrarre) i numeratori. COSÌ:

$\text{A)} \ \begin{array}{l} \cfrac{4}{x^2+2x} + \cfrac{3x-2}{x^2-x-6} = \cfrac{4}{x(x+2)} + \cfrac{3x-2}{(x+2)(x-3)} = \\[4ex] =\cfrac{4\cdot(x-3)}{x(x+2)\cdot (x-3)} + \cfrac{(3x-2)\cdot x}{(x+2)(x-3)\cdot x} = \cfrac{4\cdot(x-3) + (3x-2)\cdot x}{x(x+2)(x-3)} = \\[4ex] = \cfrac{4x-12 + 3x^2-2x}{x(x+2)(x-3)} = \cfrac{ \bm{3x^2+2x-12}}{\bm{x(x+2)(x-3)}} \end{array}$

$\text{B)} \ \begin{array}{l} \cfrac{4x}{x^3+2x^2+x} - \cfrac{2}{x^2-3x-4} = \cfrac{4x}{x(x+1)^2} - \cfrac{2}{(x+1)(x-4)}= \\[4ex] = \cfrac{4x \cdot (x-4)}{x(x+1)^2 \cdot (x-4)} - \cfrac{2 \cdot (x+1) \cdot x}{(x+1)^2(x-4)\cdot x}= \cfrac{4x \cdot (x-4) - 2 \cdot (x+1) \cdot x }{x(x+1)^2 (x-4) }= \\[4ex] = \cfrac{4x^2 -16x - 2 \cdot (x^2+x) }{x(x+1)^2 (x-4) }= \cfrac{4x^2 -16x - 2x^2 - 2x }{x(x+1)^2 (x-4) } =\\[4ex] =\cfrac{2x^2 -18x}{x(x+1)^2 (x-4)}=\cfrac{x(2x -18)}{x(x+1)^2 (x-4)}= \\[4ex] = \cfrac{\bm{2x -18}}{\bm{(x+1)^2 (x-4)}}\end{array}$

$\text{C)} \ \begin{array}{l}\cfrac{7x}{x^2-4x+4} + \cfrac{-5}{x-2}=\cfrac{7x}{(x-2)^2} + \cfrac{-5}{x-2}} = \\[4ex] = \cfrac{7x}{(x-2)^2} + \cfrac{-5\cdot (x-2)}{(x-2)\cdot (x-2)}=\cfrac{7x}{(x-2)^2} + \cfrac{-5\cdot (x-2)}{(x-2)^2}= \\[4ex] = \cfrac{7x + [-5\cdot (x-2)] }{(x-2)^2} =\cfrac{7x -5\cdot (x-2) }{(x-2)^2} = \\[4ex] = \cfrac{7x -5x+10 }{(x-2)^2} = \cfrac{ \bm{2x+10}}{\bm{(x-2)^2 } } \end{array}$

$\text{D)} \ \begin{array}{l} x +\cfrac{-3x}{x^2-4} - \cfrac{2x^3-1}{2x^2+6x+4}=\cfrac{x}{1} +\cfrac{-3x}{x^2-4} - \cfrac{2x^3-1}{2x^2+6x+4}= \\[4ex] =x +\cfrac{-3x}{(x-2)(x+2)} - \cfrac{2x^3-1}{2(x+1)(x+2)}= \\[4ex] = \cfrac{x\cdot 2(x-2)(x+2)(x+1)}{1\cdot 2(x-2)(x+2)(x+1)} \ + \ \cfrac{-3x\cdot 2(x+1)}{(x-2)(x+2)\cdot 2(x+1)} \ - \ \cfrac{(2x^3-1)\cdot(x-2)}{2(x+1)(x+2)\cdot (x+1)}= \\[4ex] = \cfrac{ 2x(x-2)(x+2)(x+1)}{2(x-2)(x+2)(x+1)} \ + \ \cfrac{-6x(x+1)}{2(x-2)(x+2)(x+1)} \ - \ \cfrac{(2x^3-1)\cdot(x-2)}{2(x-2)(x+2)(x+1)}= \\[4ex]= \cfrac{ 2x^4+2x^3-8x^2-8x}{2(x-2)(x+2)(x+1)} \ + \ \cfrac{-6x^2-6x}{2(x-2)(x+2)(x+1)} \ - \ \cfrac{2x^4-4x^3-x+2}{2(x-2)(x+2)(x+1)} = \\[4ex] = \cfrac{ 2x^4+2x^3-8x^2-8x -6x^2-6x - (2x^4-4x^3-x+2)}{2(x-2)(x+2)(x+1)} = \\[4ex] = \cfrac{ 2x^4+2x^3-8x^2-8x -6x^2-6x - 2x^4+4x^3+x-2}{2(x-2)(x+2)(x+1)} = \\[4ex] = \cfrac{ \bm{6x^3-14x^2-13x-2}}{\bm{2(x-2)(x+2)(x+1)}}\end{array}$

Esercizio 4

Risolvi le seguenti moltiplicazioni e divisioni di frazioni algebriche:

$\text{A)} \ \cfrac{x^2+5x+4}{7}\cdot \cfrac{x-1}{x^2-1}$

$\text{B)} \ \cfrac{3x^2+15x+18}{3x}\cdot \cfrac{x^2+x-2}{x^3+3x^2-x-3}$

$\text{C)} \ \cfrac{3x}{x^2+10x+25}:\cfrac{2x}{x^2-25}$

$\text{D)} \ \cfrac{x^2+8x+15}{4x}:\cfrac{x^2+4x-5}{2x^2}$

Vedi la soluzione

Per moltiplicare le frazioni algebriche, dobbiamo prima fattorizzare tutti i polinomi, poi moltiplicare tra loro i numeratori e i denominatori e infine semplificare la frazione risultante.

$\text{A)} \ \begin{array}{l} \cfrac{x^2+5x+4}{7}\cdot \cfrac{x-1}{x^2-1} = \cfrac{(x+1)(x+4)}{7}\cdot \cfrac{x-1}{(x-1)(x+1)}\\[4ex] =\cfrac{(x+1)(x+4)\cdot (x-1)}{7 \cdot (x-1)(x+1)}=\cfrac{(x+1)(x+4) (x-1)}{7(x-1)(x+1)} = \\[4ex] = \cfrac{\cancel{(x+1)}(x+4)\cancel{ (x-1)}}{7\cancel{(x-1)}\cancel{(x+1)}} = \cfrac{\bm{x+4}}{\bm{7}}\end{array}$

$\text{B)} \ \begin{array}{l}\cfrac{3x^2+15x+18}{3x}\cdot \cfrac{x^2+x-2}{x^3+3x^2-x-3} = \cfrac{3(x+2)(x+3)}{3x}\cdot \cfrac{(x-1)(x+2)}{(x-1)(x+1)(x+3)}= \\[4ex] =\cfrac{3(x+2)(x+3)\cdot (x-1)(x+2)}{3x\cdot (x-1)(x+1)(x+3)}=\cfrac{3(x+2)(x+3) (x-1)(x+2)}{3x (x-1)(x+1)(x+3)} = \\[4ex] = \cfrac{\cancel{3}(x+2)\cancel{(x+3)} \cancel{(x-1)}(x+2)}{\cancel{3}x \cancel{(x-1)}(x+1)\cancel{(x+3)}} = \cfrac{(x+2)(x+2)}{x (x+1)} = \\[4ex] = \cfrac{\bm{(x+2)^2}}{\bm{x (x+1)}}\end{array}$

Per dividere invece le frazioni algebriche prima fattorizziamo tutti i polinomi, poi moltiplichiamo trasversalmente le frazioni (il primo numeratore per il secondo denominatore e il primo denominatore per il secondo numeratore) e, infine, semplifichiamo la frazione algebrica trovata.

$\text{C)} \ \begin{array}{l} \cfrac{3x}{x^2+10x+25}:\cfrac{2x}{x^2-25}= \cfrac{3x}{(x+5)^2}:\cfrac{2x}{(x-5)(x+5)}=\\[4ex] = \cfrac{3x\cdot (x-5)(x+5)}{(x+5)^2\cdot 2x}=\cfrac{3x(x-5)(x+5)}{2x(x+5)^2 }= \\[4ex] =\cfrac{3\cancel{x}(x-5)\cancel{(x+5)}}{2\cancel{x}(x+5)^\cancel{2}} = \cfrac{\bm{3(x-5)}}{\bm{2(x+5)}}\end{array}$

$\text{D)} \ \begin{array}{l} \cfrac{x^2+8x+15}{4x}:\cfrac{x^2+4x-5}{2x^2} = \cfrac{(x+3)(x+5)}{4x}:\cfrac{(x-1)(x+5)}{2x^2}= \\[4ex] = \cfrac{(x+3)(x+5)\cdot 2x^2 }{4x \cdot (x-1)(x+5)} = \cfrac{2x^2 (x+3)(x+5)}{4x (x-1)(x+5)} = \\[4ex] = \cfrac{2x^{\cancel{2}}(x+3)\cancel{ (x+5)}}{4\cancel{x} (x-1)\cancel{ (x+5)}} =\cfrac{2x(x+3)}{4(x-1)} = \cfrac{\bm{x(x+3)}}{\bm{2(x-1)}}\end{array}$

Cosa ne pensi della spiegazione? Ti è piaciuto? Oppure hai qualche suggerimento? 💬 Raccontaci cosa ne pensi di questa pagina nei commenti! Vi leggiamo tutti! 👀 E non dimenticare che puoi farci anche tutte le tue domande! ❔👇❔👇

Frazioni algebriche: semplificazione, operazioni, esercizi risolti,…

Cosa sono le frazioni algebriche?

Frazione algebrica equivalente

Semplificare le frazioni algebriche

Operazioni con le frazioni algebriche

Addizione e sottrazione di frazioni algebriche

Somma di frazioni algebriche

Sottrazione di frazioni algebriche

Moltiplicazione di frazioni algebriche

Divisione delle frazioni algebriche

Esercizi risolti sulle frazioni algebriche

Esercizio 1

Esercizio 2

Esercizio 3

Esercizio 4

Lascia un commento Annulla risposta