Le frazioni o i numeri misti sono espressioni numeriche che indicano una quantità divisa per un’altra. Si tratta quindi di un valore rappresentato dal quoziente di due numeri. Con questo tipo di numeri possiamo esprimere quantità decimali e intere e possiamo anche indicare delle proporzioni . Successivamente, definiremo le frazioni in modo più matematico e ti mostreremo alcuni esempi, in modo che tu possa comprendere questo concetto graficamente.
Cosa sono le frazioni?
Una frazione è uguale al numero di parti che prendiamo da un’unità divisa in parti uguali. Quindi, graficamente, è rappresentato da due termini separati da una linea orizzontale al centro. Più precisamente, in cima alla riga troviamo il numeratore e sotto il denominatore.
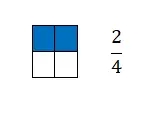
Come puoi vedere, le frazioni sono un concetto matematico molto semplice da rappresentare graficamente perché vanno di pari passo con le proporzioni. Ecco perché nell’esempio precedente abbiamo espresso il numero di quadrati colorati con un numero frazionario.
Termini frazionari
Le due parti della frazione sono:
- Numeratore: questo termine si trova sopra la linea orizzontale ed è qui che scriviamo il numero di pezzi che prendiamo. Possiamo trovare numeratori positivi, negativi e zero (uguali a zero).
- Denominatore: quest’altro termine si trova sotto la linea ed è qui che scriviamo il numero totale di parti in cui è divisa l’unità. Possiamo trovare denominatori positivi e negativi, ma questi non possono essere zero.
tipi di frazioni
Esistono molti tipi di frazioni, a seconda dei numeri che le compongono e dell’equivalenza che presentano con le altre frazioni. Successivamente definiremo tutte le categorie esistenti e commenteremo le caratteristiche che consentono di differenziarle dalle altre:
- Frazioni proprie: sono quelle formate da un numeratore inferiore al denominatore. Se converti queste frazioni in un decimale , otterrai un numero compreso tra zero e uno. Non può essere maggiore di uno, perché il valore del numeratore sarà sempre inferiore a quello del denominatore e, quindi, non verrà superata l’unità.
- Frazioni improprie: sono quelle che hanno un numeratore maggiore del denominatore, in questo caso esprimono valori numerici maggiori dell’unità. Ad esempio, 8/5 è uguale a 1,6 che è maggiore di 1. Questi sono un altro modo di esprimere numeri misti, che sono del tipo seguente.
- Frazioni miste: chiamate anche numeri misti, sono quelle composte da un numero intero e da un numero misto. In pratica si rappresentano con il valore intero prima della frazione, quindi per convertirle in frazioni improprie occorre moltiplicare la parte intera per il denominatore, sommarla al numeratore e lasciare invariato il denominatore.
- Frazioni decimali: sono quelle che hanno un denominatore che esprime una quantità equivalente a una potenza di dieci, ad esempio: 6/10, 34/1000 o 5/100. Questi vengono utilizzati nella notazione decimale e sono più comuni quando si convertono numeri decimali esatti in numeri misti. Ne discuteremo più dettagliatamente nella sezione successiva.
- Frazioni composte: sono quelle che sono composte da un’altra frazione, o al numeratore, o al denominatore, o a entrambi. Quindi per semplificare queste espressioni e mostrarle come una singola frazione, dobbiamo dividere il numeratore per il denominatore. Ciò diventerà più chiaro una volta spiegata la divisione tra frazioni.
- Frazioni equivalenti: sono quelle che equivalgono allo stesso numero, sebbene non siano costituite dagli stessi numeratori o denominatori. Ad esempio, 8/4 = 4/2 = 2, entrambe le frazioni sono uguali a due. In questo caso specifico è perché la prima frazione è uguale al doppio della seconda, quindi mantiene un rapporto proporzionale.
- Frazioni irriducibili: sono quelle che non possono essere ulteriormente semplificate, perché il numeratore e il denominatore non condividono fattori comuni e, quindi, non possono essere divisi per nessun numero. Alcuni esempi di questo tipo sono: 9/5, 5/6, 7/8, tra gli altri. Per sapere come rilevarli, è importante sapere come calcolare il massimo comun divisore .
Operazioni con le frazioni
Ora che conosciamo le diverse categorie di frazioni esistenti, vedremo come risolvere le diverse operazioni aritmetiche con numeri misti . Va notato che questo è un po’ più complicato delle operazioni con i numeri interi, anche se una volta compresa la metodologia, tutto diventa abbastanza semplice. Inoltre, non solo spiegheremo la teoria, ma vi mostreremo anche alcuni esempi. Detto questo, cominciamo.
somma di frazioni
Sommare frazioni con un denominatore comune è abbastanza semplice, poiché basta sommare i due numeratori e lasciare lo stesso denominatore. D’altra parte, sommare frazioni con denominatori diversi diventa un po’ complicato, perché devi trovare il minimo comune multiplo dei denominatori. E poi, dobbiamo aggiungere il prodotto di ciascun numeratore dividendo lcm (il nuovo denominatore) per il vecchio denominatore. Per comprendere meglio è possibile osservare il seguente diagramma:
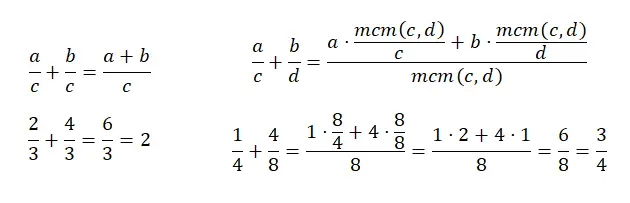
frazioni di sottrazione
La sottrazione di frazioni con denominatore comune è molto simile all’addizione, infatti tutto si fa allo stesso modo tranne che nella somma dei numeratori, perché invece di aggiungere bisogna sottrarre. E nella sottrazione di frazioni con denominatori diversi accade la stessa cosa, è praticamente la stessa cosa tranne che invece di sommare il prodotto dei numeratori dividendo lcm per il vecchio denominatore, dobbiamo sottrarre . Ecco un altro diagramma:
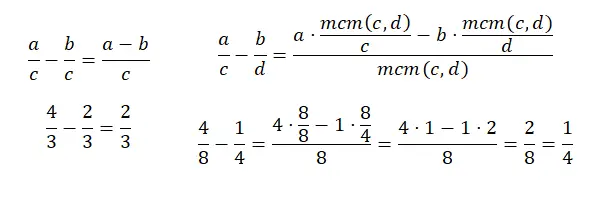
moltiplicazione di frazioni
La moltiplicazione delle frazioni può essere risolta allo stesso modo indipendentemente dal fatto che i denominatori siano gli stessi o meno. Fondamentalmente devi moltiplicare i numeratori per una parte e i denominatori per un’altra. Questa è forse l’operazione più semplice, poiché basta eseguire solo due moltiplicazioni.
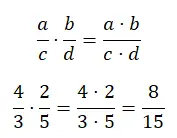
divisione delle frazioni
Anche la divisione in frazioni è abbastanza semplice da risolvere, basta moltiplicare le croci. In altre parole, il numeratore è il risultato della moltiplicazione del numeratore della prima frazione per il denominatore della seconda. mentre il denominatore è il prodotto del denominatore della prima frazione e del numeratore della seconda.
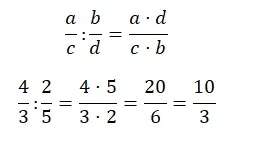
Semplificare le frazioni
Semplificare le frazioni o ridurre le frazioni non è un’operazione aritmetica in quanto tale, ma è molto importante sapere come farlo ed inoltre è un argomento che abbiamo già trattato un po’ con i tipi di frazioni. Quindi, per semplificare un numero misto, dobbiamo dividere numeratore e denominatore per lo stesso numero. In generale, per effettuare questa semplificazione sceglieremo il massimo fattore comune . Nell’immagine seguente potete trovare un esempio.
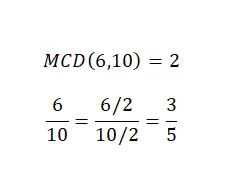
Come puoi vedere, abbiamo due frazioni equivalenti , quindi entrambe rappresentano lo stesso valore numerico, ma la seconda è più semplice della prima. Pertanto, abbiamo raggiunto con successo l’obiettivo della semplificazione.
Come passare dal decimale alla frazione e viceversa?
La frazione generatrice è la frazione irriducibile ottenuta da un numero decimale, sia esso un numero decimale esatto o un numero decimale periodico. Naturalmente dovremo utilizzare metodi diversi a seconda del tipo di decimale, di cui parleremo più avanti.
Converti da decimale esatto a frazione generatrice
In questo caso possiamo ricorrere alle frazioni decimali che abbiamo commentato all’inizio. Semplicemente dobbiamo scrivere il valore numerico al numeratore, ma senza la virgola decimale. Mentre al denominatore scriviamo la potenza di dieci che ha tanti zeri quante sono le cifre del numeratore.
Tuttavia, se abbiamo un numero decimale maggiore di uno, come 4,25, allora dovremo moltiplicare il numero di unità complete che abbiamo per il valore del denominatore e aggiungerlo al numeratore originale. Di seguito troverai un esempio di ciascuna tipologia:
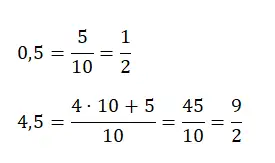
Converti i decimali ripetuti puri in frazioni generatrici
Quando abbiamo un numero decimale periodico puro , se vogliamo ottenere la frazione generatrice, dovremo mettere al numeratore lo stesso valore, ma senza punto decimale e sottrarre la parte intera. Anche se il denominatore sarà uguale a un numero composto da soli nove, dobbiamo scrivere espressamente tanti nove quante sono le cifre della parte decimale del numero originale. Questo sistema crea un po’ di confusione, ma con alcuni esempi capiremo:
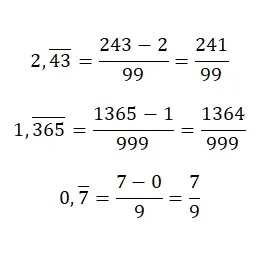
Converti decimali ripetuti misti in frazioni generatrici
Nel caso in cui si abbia un numero decimale ripetuto misto , dovremo applicare una regola abbastanza complessa. Per prima cosa scriveremo il numero senza la virgola al numeratore e sottrarre la parte intera seguita dai decimali non ricorrenti, anch’essi senza virgola. Per quanto riguarda il denominatore, dovrai scrivere tanti nove quante sono le cifre della parte decimale periodica, seguiti da tanti zeri quante sono le cifre della parte decimale non ricorrente.
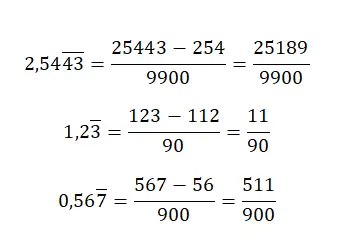
convertire la frazione in decimale
Per passare da una frazione a un decimale è sufficiente dividere il numeratore per il denominatore, perché un numero misto non è altro che il quoziente tra due valori . Quindi, risolvendo la divisione, ottieni il numero decimale corrispondente. Nell’immagine seguente puoi trovare alcuni esempi abbastanza semplici:
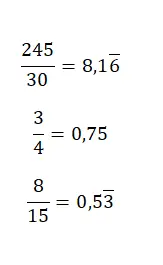
esercizi sulle frazioni
Ora che conosci tutta la teoria sulle frazioni, ti consigliamo di svolgere alcuni esercizi. In questo modo imparerai tutti i concetti spiegati in modo più approfondito e il giorno dell’esame andrai più veloce nella risoluzione dei calcoli. Inoltre, avrai visto tutti i tipi di esercizi sulle frazioni esistenti e saprai come risolverli di conseguenza. Infine, lascia che ti dica che abbiamo a tua disposizione anche un calcolatore di frazioni online, con il quale potrai risolvere tutte le operazioni sulle frazioni.