Formula per la distanza tra due punti (geometria)

In questa pagina troverai come calcolare la distanza tra due punti in geometria (formula). Potrai anche vedere esempi e, inoltre, esercitarti con esercizi risolti sulla distanza tra due punti.

Qual è la formula per la distanza tra due punti?

La distanza tra due punti è uguale alla lunghezza del segmento che li unisce. Quindi in matematica, per determinare la distanza tra due punti diversi, dobbiamo calcolare i quadrati delle differenze tra le loro coordinate e poi trovare la radice della somma di detti quadrati.

In altre parole, la formula utilizzata per calcolare la distanza tra due punti diversi del piano cartesiano è la seguente:

Consideriamo le coordinate di due punti distinti:

$A(x_1,y_1) \qquad \qquad B(x_2,y_2)$

La formula per la distanza tra due punti è:

$d(A,B) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2 \vphantom{\frac{1}{2}}}$

Questa formula deriva dalla grandezza di un vettore. In effetti, ciò che stiamo facendo con questa formula è in realtà calcolare l’ampiezza del vettore determinato dai due punti in questione. Puoi leggere di più a questo proposito nella spiegazione di cosa è il modulo di un vettore .

D’altra parte, in geometria analitica la dimostrazione della formula per la distanza tra due punti può essere fatta anche utilizzando il teorema di Pitagora:

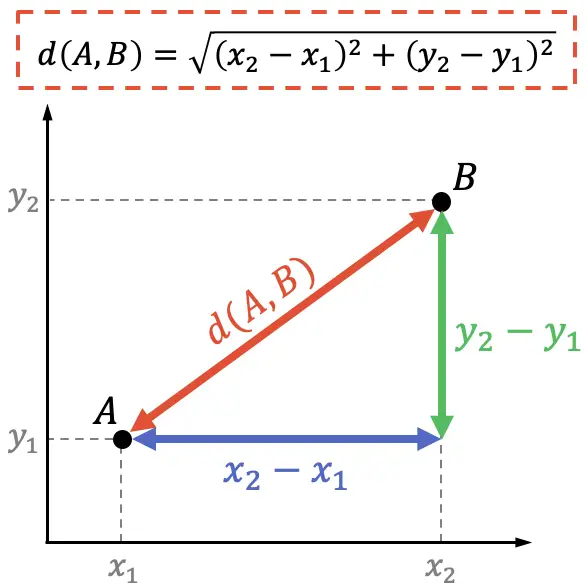
Il teorema di Pitagora afferma che il quadrato dell’ipotenusa di un triangolo rettangolo equivale alla somma dei quadrati dei suoi cateti, quindi:

$\bigl(d(A,B)\bigr)^2 = (x_2-x_1)^2 + (y_2-y_1)^2$

E per ottenere la formula devi solo trovare la distanza tra i 2 punti:

$d(A,B) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2 \vphantom{\frac{1}{2}}}$

Infine, vale la pena notare che, se lavorassimo con punti a 3 coordinate, la formula per la distanza tra due punti nello spazio (in R3) sarebbe la stessa ma aggiungendo la coordinata Z:

$d(A,B) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2 \vphantom{\frac{1}{2}}}$

Esempio di calcolo della distanza tra due punti

Una volta vista la definizione della formula per la distanza tra due punti, vediamo ora come determinare detta distanza utilizzando un esempio:

Trova la distanza tra i due punti seguenti:

$A(-1,7) \qquad \qquad B(3,4)$

Per trovare geometricamente la distanza tra i due punti è sufficiente applicare la formula:

$d(A,B) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2 \vphantom{\frac{1}{2}}}$

Ora sostituiamo le coordinate dei punti nella formula:

$d(A,B) = \sqrt{(3-(-1))^2+(4-7)^2 \vphantom{\frac{1}{2}}}$

E facciamo i calcoli:

$\begin{aligned} d(A,B) &= \sqrt{(3+1)^2+(4-7)^2 \vphantom{\frac{1}{2}}} \\[2ex] &= \sqrt{4^2+(-3)^2 \vphantom{\frac{1}{2}}} \\[2ex] &= \sqrt{16+9}\\[2ex] &= \sqrt{25}\\[2ex] & = \bm{5}\end{aligned}$

La distanza tra i due punti è quindi pari a 5 unità.

Ovviamente il valore della distanza deve darci sempre segno positivo, perché le distanze sono sempre positive. Altrimenti significa che abbiamo commesso un errore in un passaggio.

Risoluzione dei problemi relativi alla distanza tra due punti

Esercizio 1

Calcola la distanza tra i seguenti due punti:

$A(4,2) \qquad \qquad B(1,5)$

vedi soluzione

Per trovare la distanza geometrica tra i due punti è sufficiente utilizzare la formula:

$d(A,B) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2 \vphantom{\frac{1}{2}}}$

Ora sostituiamo le coordinate dei punti nella formula:

$d(A,B) = \sqrt{(1-4)^2+(5-2)^2 \vphantom{\frac{1}{2}}}$

E facciamo i calcoli:

$\begin{aligned} d(A,B) & = \sqrt{(-3)^2+3^2 } \\[2ex] & = \sqrt{9+9 } \\[2ex] & = \bm{\sqrt{18}} \end{aligned}$

Esercizio 2

Trova la distanza tra i due punti seguenti:

$A(8,6) \qquad \qquad B(-4,1)$

vedi soluzione

Per trovare la distanza matematica tra i due punti, dobbiamo utilizzare la formula corrispondente:

$d(A,B) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2 \vphantom{\frac{1}{2}}}$

Ora sostituiamo le coordinate dei punti nella formula:

$d(A,B) = \sqrt{(-4-8)^2+(1-6)^2 \vphantom{\frac{1}{2}}}$

E facciamo i calcoli:

$\begin{aligned} d(A,B) &= \sqrt{(-12)^2+(-5)^2 } \\[2ex] &= \sqrt{144+25 }\\[2ex] &= \sqrt{169} \\[2ex] &= \bm{13}\end{aligned}$

Esercizio 3

Calcola il perimetro del triangolo formato dai punti A, B e C rappresentato graficamente qui sotto:

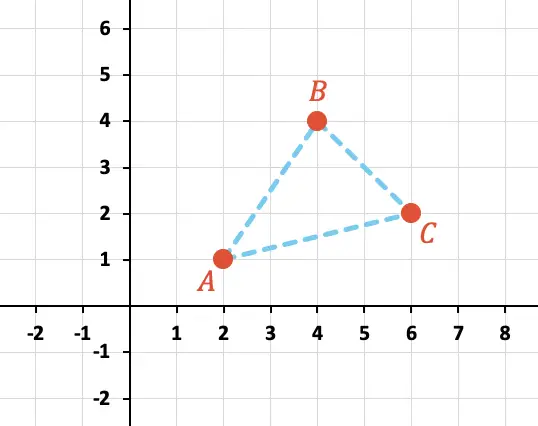
esercizio risolto della distanza tra due punti

vedi soluzione

Per prima cosa dobbiamo identificare le coordinate X e Y di ciascun punto sul grafico:

$A(2,1)$

$B(4,4)$

$C(6,2)$

E ora dobbiamo calcolare la distanza tra tutti i punti con la formula:

$d(A,B) = \sqrt{(4-2)^2+(4-1)^2 } = \sqrt{4+9} =\sqrt{13} = 3,61$

$d(A,C) = \sqrt{(6-2)^2+(2-1)^2 } = \sqrt{16+1} =\sqrt{17} = 4,12$

$d(B,C) = \sqrt{(6-4)^2+(2-4)^2 } = \sqrt{4+4} =\sqrt{8} = 2,83$

Quindi il perimetro del triangolo sarà la somma della lunghezza dei 3 lati:

$P=3,61+4,12+2,83= \bm{10,56}$

Esercizio 4

Controlla se il triangolo i cui vertici sono i punti A, B e C è un triangolo isoscele. Ma i tre punti:

$A(-4,5) \qquad B(7,-5) \qquad C(10,0)$

vedi soluzione

Perché un triangolo sia isoscele è necessario che due dei suoi lati siano uguali. Dobbiamo quindi trovare la lunghezza di ciascuno dei suoi lati, che corrisponde alle distanze tra i suoi vertici.

Calcoliamo quindi la distanza tra i vertici del triangolo:

$d(A,B) = \sqrt{(7-(-4))^2+(-5-5)^2 } = \sqrt{11^2+(-10)^2} = \sqrt{221}$

$d(A,C) = \sqrt{(10-(-4))^2+(0-5)^2 } = \sqrt{14^2+(-5)^2} = \sqrt{221}$

$d(B,C) = \sqrt{(10-7)^2+(0-(-5))^2} = \sqrt{3^2+5^2} = \sqrt{34}$

Quindi il triangolo ha 2 lati identici e il terzo lato misura diversamente dagli altri due, quindi è effettivamente un triangolo isoscele.

Esercizio 5

Trova un punto sull’asse Y equidistante dai due punti seguenti:

$A(5,-3) \qquad \qquad B(-2,4)$

vedi soluzione

Innanzitutto se il punto si trova sull’asse del computer (asse OY) significa che l’ascissa del punto è zero:

$P(0,y)$

In secondo luogo, se il punto è equidistante dai punti A e B, ciò implica che è soddisfatta la seguente equazione:

$d(P,A)= d(P,B)$

Quindi, utilizzando la formula per la distanza tra due punti, possiamo trovare il valore della variabile y dall’equazione precedente:

$\sqrt{(5-0)^2+(-3-y)^2 \vphantom{\frac{1}{2}}}=\sqrt{(-2-0)^2+(4-y)^2 \vphantom{\frac{1}{2}}}$

Poiché entrambi i lati dell’equazione hanno una radice, possiamo semplificarli:

$5^2+(-3-y)^2=(-2)^2+(4-y)^2$

Risolviamo i poteri e le uguaglianze notevoli (o prodotti notevoli):

$25+9+y^2+6y=4+16+y^2-8y$

E operiamo finché non troviamo il valore dell’incognita y :

$y^2+6y-y^2+8y=4+16-25-9$

$14y=-14$

$y=\cfrac{-14}{14}$

$y=-1$

In breve, il punto che ci pone la dichiarazione del problema è:

$\bm{P(0,-1)}$

Se hai trovato utile questo articolo, probabilmente ti interesseranno anche degli esercizi sulla distanza tra un punto e una retta . Nella pagina collegata troverai non solo esercizi risolti passo dopo passo, ma anche una spiegazione dettagliata del calcolo della distanza tra punti e linee, esempi e applicazione della formula della distanza tra un punto e una linea per determinare un altro tipo di distanza .

Qual è la formula per la distanza tra due punti?

Esempio di calcolo della distanza tra due punti

Risoluzione dei problemi relativi alla distanza tra due punti

Esercizio 1

Esercizio 2

Esercizio 3

Esercizio 4

Esercizio 5

Lascia un commento Annulla risposta