▷ Come calcolare il punto medio di un segmento? (formula)

Questa pagina spiega il significato del punto medio di un segmento. Inoltre, scoprirai come trovare la metà di un segmento utilizzando la sua formula. Vedrai anche esempi, esercizi e problemi risolti sui punti medi dei segmenti.

Qual è il punto medio di un segmento?

In matematica, il punto medio di un segmento è il punto situato alla stessa distanza dagli estremi del segmento. La parte centrale quindi divide il segmento in due parti uguali.

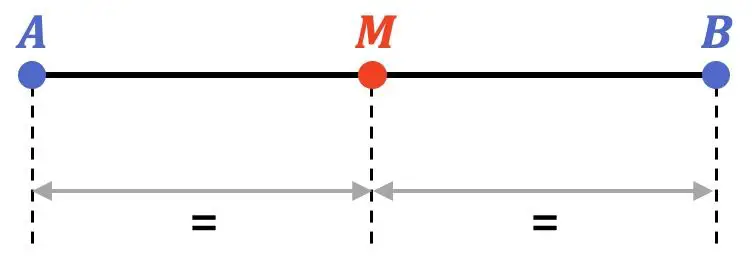
Inoltre, il punto medio è proprio al centro del segmento, quindi appartiene alla bisettrice del segmento.

D’altra parte, il punto medio di un segmento è anche un punto equidistante da due elementi geometrici: le due estremità del segmento.

Come calcolare il punto medio di un segmento?

Date le coordinate cartesiane dei punti estremi di un segmento:

$A(x_1,y_1) \qquad B(x_2,y_2)$

Le coordinate del centro di detto segmento corrispondono alla semisomma delle coordinate dei punti estremi:

$\displaystyle M\left(\frac{x_1+x_2}{2} , \frac{y_1+y_2}{2} \right)$

Questa è la formula per calcolare il centro di un segmento nel piano cartesiano (in R2). Ma ovviamente la formula è applicabile anche allo spazio cartesiano (in R3), basta aggiungere la metà della somma della coordinata Z:

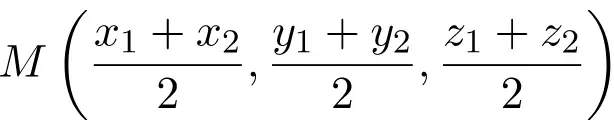
Vediamo un esempio di come calcolare le coordinate del punto medio di un segmento:

Determinare il punto medio del segmento formato dai seguenti punti:

$A(2,5) \qquad B(4,-1)$

Per trovare il centro del segmento, applica semplicemente la sua formula:

$\displaystyle M\left(\frac{x_1+x_2}{2} , \frac{y_1+y_2}{2} \right)$

$\displaystyle M\left(\frac{2+4}{2} , \frac{5+(-1)}{2} \right)$

$\displaystyle M\left(\frac{6}{2} , \frac{4}{2} \right)$

$\displaystyle \bm{M\left(3,2\right)}$

Esercizi risolti a metà di un segmento

Esercizio 1

Qual è il punto medio del segmento i cui estremi sono i due punti seguenti?

$A(3,-2) \qquad B(5,8)$

Vedi la soluzione

Per trovare la metà del segmento devi applicare direttamente la formula:

$\displaystyle M\left(\frac{x_1+x_2}{2} , \frac{y_1+y_2}{2} \right)$

$\displaystyle M\left(\frac{3+5}{2} , \frac{-2+8}{2} \right)$

$\displaystyle M\left(\frac{8}{2} , \frac{6}{2} \right)$

$\displaystyle \bm{M\left(4,3\right)}$

Esercizio 2

Trova le coordinate del punto finale del segmento che inizia nel punto A e il cui punto medio è M.

$A(4,-1) \qquad M(-2,1)$

Vedi la soluzione

In questo caso conosciamo le coordinate del punto iniziale e del centro del segmento. Pertanto, sostituiamo nella formula le coordinate che conosciamo per il punto medio di un segmento:

$\displaystyle \left(\frac{x_1+x_2}{2} , \frac{y_1+y_2}{2} \right)=(x_m,y_m)$

$\displaystyle \left(\frac{4+x_2}{2} , \frac{-1+y_2}{2} \right)=(-2,1)$

E ora risolviamo le coordinate del punto finale del segmento dall’equazione precedente:

Coordinate X

$\cfrac{4+x_2}{2} = -2$

$4+x_2 = -2 \cdot 2$

$4+x_2 = -4$

$x_2 = -4-4$

$x_2 = -8$

Coordinate Y

$\cfrac{-1+y_2}{2} = 1$

$-1+y_2 = 1 \cdot 2$

$-1+y_2 = 2$

$y_2 = 2+1$

$y_2 = 3$

Le coordinate dell’estremità finale del segmento sono quindi:

$\bm{B(-8,3)}$

Esercizio 3

Dato il seguente parallelogramma:

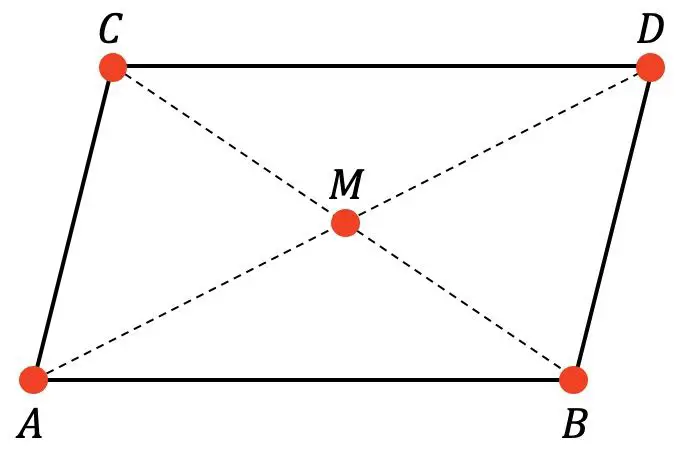
Sappiamo che M è il centro del parallelogramma e le coordinate dei punti A, B e C sono:

$A(1,1) \quad B(5,1) \quad C(7,3)$

Da queste informazioni e utilizzando la formula del punto medio, calcola le coordinate del punto D.

Vedi la soluzione

Per trovare le coordinate del punto D utilizzando la formula del centro di un segmento, devi prima calcolare le coordinate del punto M e poi quelle del punto D.

Il punto M è il punto medio del segmento BC, le sue coordinate sono quindi:

$\displaystyle M\left(\frac{5+7}{2} , \frac{1+3}{2} \right)$

$\displaystyle M\left(6,2 \right)$

E una volta conosciuto il punto M, possiamo trovare il punto D. Il punto M è anche il centro del segmento AD, quindi:

$\displaystyle \left(\frac{1+x_2}{2} , \frac{1+y_2}{2} \right)=(6,2)$

Coordinata X del punto D

$\cfrac{1+x_2}{2} = 6$

$1+x_2 = 12$

$x_2 = 11$

Coordinata Y del punto D

$\cfrac{1+y_2}{2} = 2$

$1+y_2 = 4$

$y_2 = 3$

Le coordinate del punto D sono quindi:

$\bm{D(11,3}$

Esercizio 4

Calcola l’equazione continua della retta perpendicolare al segmento PQ nel suo punto medio. Sii i punti

$P(1,4)$

$Q(5,-2).$

Vedi la soluzione

Per determinare l’equazione di una linea, abbiamo bisogno del suo vettore direzione e di un punto che faccia parte della linea.

In questo caso, il vettore direzione della linea sarà perpendicolare al vettore

$\vv{PQ}.$

Calcoliamo quindi il vettore

$\vv{PQ}:$

$\vv{PQ} = Q - P = (5,-2)-(1,4) = (4,-6)$

E possiamo trovare un vettore perpendicolare ad un altro cambiando le componenti del vettore tra di loro e poi cambiando il segno di una componente, quindi:

$\vv{PQ}_\perp =(6,4)$

Ora abbiamo il vettore direzione della linea, quindi abbiamo bisogno solo di un punto appartenente alla linea. In questo caso l’istruzione ci dice che la retta passa per il punto medio del segmento, quindi calcoliamo il punto medio utilizzando la formula:

$\displaystyle M\left(\frac{1+5}{2} , \frac{4+(-2)}{2} \right)$

$\displaystyle M\left(3,1 \right)$

Infine, costruiamo l’equazione continua della retta dal punto e dal vettore calcolati:

$\cfrac{x-3}{6}=\cfrac{y-1}{4}$

Formula per la metà di un segmento

Qual è il punto medio di un segmento?

Come calcolare il punto medio di un segmento?

Esercizi risolti a metà di un segmento

Esercizio 1

Esercizio 2

Esercizio 3

Esercizio 4

Lascia un commento Annulla risposta