Pendenza di una retta (formula)

In questa pagina troverai la spiegazione più dettagliata della pendenza di una linea: qual è la sua formula, esempi di calcolo, cosa significa il concetto di pendenza di una linea,… Potrai anche vedere come identificare facilmente la pendenza di una linea dalla sua equazione e, inoltre, potrai esercitarti con esercizi risolti passo dopo passo.

Formula per la pendenza di una retta

La pendenza di una linea è uguale allo spostamento verticale tra due punti diviso per lo spostamento orizzontale tra questi stessi due punti.

Cioè, dati due punti su una linea:

$P_1(x_1,y_1) \qquad P_2(x_2,y_2)$

La formula per la pendenza di una retta è:

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{y_2-y_1}{x_2-x_1}$

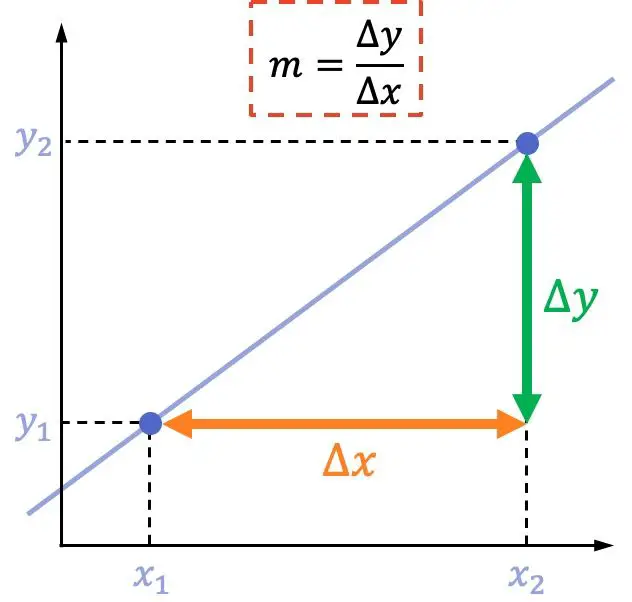
Esempio di calcolo della pendenza di una retta partendo da due punti

Successivamente vedremo un esempio di come viene calcolata la pendenza di una linea con la formula:

Calcola la pendenza della retta che passa per i seguenti due punti:

$P_1(3,1) \qquad P_2(5,7)$

Per trovare la pendenza di questa linea, applica semplicemente la sua formula:

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{y_2-y_1}{x_2-x_1}=\cfrac{7-1}{5-3}=\cfrac{6}{2} = \bm{3}$

La pendenza della retta è quindi pari a 3.

Trovare la pendenza di una retta dalla sua equazione

Nella sezione precedente abbiamo appena visto come determinare numericamente la pendenza di una retta. Non sempre però è necessario fare calcoli, ma il suo valore può essere individuato anche dall’equazione di una retta. Ogni tipo di equazione è diversa, quindi analizzeremo ciascun caso separatamente.

Pendenza data l’equazione esplicita della retta

L’equazione esplicita della retta segue la seguente espressione:

$y =\color{blue}\bm{m}\color{black}x+n$

Quindi il parametro

$m$

corrisponde alla pendenza della retta.

Pendenza data l’equazione punto-pendenza della retta

La formula per l’equazione punto-pendenza della retta è la seguente:

$y -y_0=\color{blue}\bm{m}\color{black}(x-x_0)$

Come prima, il coefficiente

$m$

corrisponde alla pendenza della retta.

Pendenza data l’equazione implicita della retta

Data l’equazione implicita della retta (detta anche equazione generale o cartesiana):

$Ax+By+C=0$

La pendenza della retta può essere trovata facendo:

$m=-\cfrac{A}{B}$

Pendenza tenendo conto del vettore direzione della retta

Il vettore direzione della linea è il vettore che ne segna la direzione. Quindi, se il vettore direzione di una linea è:

$\vv{\text{v}}= (\text{v}_1,\text{v}_2)$

La pendenza di questa retta è:

$m=\cfrac{\text{v}_2}{\text{v}_1}$

pendenza dato un angolo

Infine, se una linea forma un angolo

$\alpha$

nella parte positiva dell’asse delle ascisse (asse X), la sua pendenza è equivalente alla tangente dell’angolo:

$m = \text{tg}(\alpha)$

Significato della pendenza di una retta

Con tutte le informazioni di cui sopra, sappiamo già perfettamente come trovare la pendenza di una retta. Ma in realtà… cosa significa la pendenza di una retta?

La pendenza di una linea indica le unità verticali in cui la linea sale per ciascuna unità orizzontale del grafico.

Ad esempio, nella rappresentazione della linea seguente, puoi vedere che essa avanza di 2 unità verticali per ogni unità orizzontale, perché la sua pendenza è pari a 2.

Inoltre, la pendenza di una linea ne indica anche la pendenza:

Se una linea è crescente (ascendente), la sua pendenza è positiva.
Se una linea è decrescente (discendente), la sua pendenza è negativa.
Se una linea è completamente orizzontale, la sua pendenza è pari a 0.
Se una linea è completamente verticale, la sua pendenza è uguale a infinito.

pendenza di una linea positiva o negativa

Posizione relativa delle linee

D’altro canto la posizione relativa tra due linee può essere conosciuta anche dalle proprietà dei pendii:

Se due rette hanno pendenze diverse significa che si intersecano , cioè si intersecano in un punto.

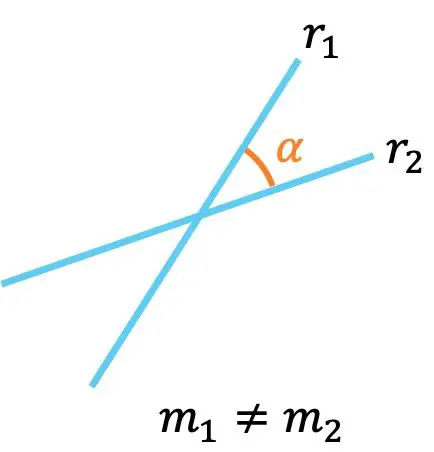
linee che si intersecano pendii distinti

Inoltre, l’angolo tra le due linee attraverso le loro pendenze può essere calcolato con la seguente formula:

$\text{tg}(\alpha) = \cfrac{m_2-m_1}{1+m_1\cdot m_2}$

In secondo luogo, se due rette hanno la stessa pendenza, ciò implica che sono parallele .

Infine, le pendenze di due linee perpendicolari o ortogonali (che formano 90º) soddisfano la seguente condizione:

Questo è un modo per scoprire se due linee sono parallele o perpendicolari tra loro, tuttavia esistono altri metodi e alcuni sono anche più veloci. Per saperne di più puoi andare alla spiegazione di perpendicolarità e parallelismo tra linee . Inoltre, queste pagine spiegano anche come trovare una linea perpendicolare (o parallela) ad un’altra.

Risolti problemi di pendenza di una retta

Esercizio 1

Trova la pendenza della retta che passa per i due punti seguenti:

$P_1(5,6) \qquad P_2(8,3)$

vedi soluzione

Per calcolare la pendenza della linea, è necessario utilizzare la formula:

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{y_2-y_1}{x_2-x_1}=\cfrac{3-6}{8-5}=\cfrac{-3}{3} = \bm{-1}$

Esercizio 2

Calcola la pendenza della retta che passa per i seguenti due punti:

$P_1(-3,1) \qquad P_2(-2,-4)$

vedi soluzione

Per trovare la pendenza della retta è necessario utilizzare la formula:

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{y_2-y_1}{x_2-x_1}=\cfrac{-4-1}{-2-(-3)}=\cfrac{-5}{-2+3}=\cfrac{-5}{1} = \bm{-5}$

Esercizio 3

Qual è la pendenza di ciascuna linea?

$\begin{array}{lll} A) \ y= 2x+3 & \qquad & B) \ y-3=4(x+1) \\[2ex] C) \ 6x+2y-7=0 & \qquad & D) \ \begin{cases}x=3-t \\[2ex] y=1+2t \end{cases} \end{array}$

vedi soluzione

A) La retta è espressa come un’equazione implicita, quindi la sua pendenza è 2 (il termine che accompagna la

$x$

B) La linea è definita dalla sua equazione punto-pendenza, quindi la sua pendenza è 4 (il numero prima delle parentesi).

C) La retta è in forma di equazione implicita, quindi la sua pendenza è:

$m= - \cfrac{A}{B} = -\cfrac{6}{2} = \bm{-3}$

D) La retta è definita sotto forma di equazioni parametriche, quindi dobbiamo prima trovare il suo vettore direzione e con esso possiamo calcolare la pendenza della retta. Pertanto, le componenti del vettore di direzione sono i termini che accompagnano il coefficiente

$t:$

$\vv{\text{v}} = (-1,2)$

E una volta conosciuto il vettore direzione della retta, possiamo determinare la pendenza della retta:

$m = \cfrac{\text{v}_2}{\text{v}_1} = \cfrac{2}{-1} = \bm{-2}$

Esercizio 4

Determinare la pendenza di ciascuna linea rappresentata nel grafico:

Equazione esplicita dell'esercizio della retta risolto passo dopo passo

vedi soluzione

blu a destra

La linea blu aumenta di una Y per ogni X, quindi la sua pendenza è uguale a 1.

$m=1$

verde giusto

La linea verde aumenta di tre Y per ogni X, quindi la sua pendenza è 3 .

$m=3$

linea rossa

La linea rossa diminuisce di due Y per ogni X, quindi la sua pendenza è pari a -2 .

$m=-2$

Formula per la pendenza di una retta

Esempio di calcolo della pendenza di una retta partendo da due punti

Trovare la pendenza di una retta dalla sua equazione

Pendenza data l’equazione esplicita della retta

Pendenza data l’equazione punto-pendenza della retta

Pendenza data l’equazione implicita della retta

Pendenza tenendo conto del vettore direzione della retta

pendenza dato un angolo

Significato della pendenza di una retta

Posizione relativa delle linee

Risolti problemi di pendenza di una retta

Esercizio 1

Esercizio 2

Esercizio 3

Esercizio 4

Lascia un commento Annulla risposta