Binomio di newton (teorema binomiale)

In questa pagina troverai la spiegazione di cos’è il binomio (o teorema binomiale) di Newton e qual è la sua formula. Puoi anche vedere come questo può essere semplificato con il triangolo di Tartaglia (o Pascal). Inoltre, troverai esercizi risolti passo passo per il binomio di Newton e tutte le sue proprietà. Infine, spiegheremo le curiosità dietro l’origine di questo particolarissimo teorema.

Cos’è il binomio di Newton?

In matematica, il binomio di Newton , noto anche come teorema del binomio , è una formula che permette di calcolare facilmente la potenza di un binomio. In altre parole, il binomio di Newton consiste in una formula con la quale si possono risolvere espressioni algebriche della forma (a+b).

Ovviamente, questo teorema prende il nome dal fisico, matematico e filosofo Sir Isaac Newton. Vi sono tuttavia alcune controversie a questo riguardo poiché sono stati ritrovati testi mediorientali in cui questo teorema era già in uso. Di seguito discuteremo in modo approfondito l’origine di questa formula matematica.

La formula binomiale di Newton

Come abbiamo visto nella definizione del binomio di Newton, questo teorema viene utilizzato per risolvere le potenze dei binomi. Ma… come si applica il binomio di Newton? O, in altre parole, qual è la formula binomiale di Newton?

La formula matematica per il binomio di Newton è la seguente:

\displaystyle \left( a+b\right)^n = & \sum_{k=0}^{n}\begin{pmatrix} n\\ k\end{pmatrix}a^{n-k}b^k

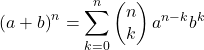
O equivalente:

\left( a+b\right)^n =\begin{pmatrix} n \\ 0 \end{pmatrix} \right)a^n b^0 + \begin{pmatrix} n \\ 1 \end{pmatrix} a^{n-1}b^{1} + \begin{pmatrix} n \\ 2 \end{pmatrix} a^{n-2}b^{2} + \dots + \begin{pmatrix} n \\ n \end{pmatrix} a^0 b^{n}

La formula è un po’ complessa per comprendere il concetto del binomio di Newton, quindi abbiamo presentato di seguito le potenze dei binomi di grado più basso in modo che tu possa capirla meglio:

formula del teorema binomiale di Newton

Come puoi vedere, quando si espande un binomio , gli esponenti del primo termine (a) diminuiscono mentre aumentano gli esponenti del secondo termine (b) , così come aumenta l’elemento inferiore dei numeri combinatori.

Pertanto, per utilizzare il teorema binomiale, è necessario sapere risolvere un numero combinatorio, cioè l’espressione algebrica del tipo

\begin{pmatrix} 4 \\ 2 \end{pmatrix}

. Quindi, prima di esaminare esempi su come calcolare un binomio di Newton, esaminiamo brevemente i numeri combinatori.

numero combinatorio

Per determinare un numero combinatorio (o coefficiente binomiale) è necessario applicare la seguente formula:

\begin{pmatrix}n \\ k \end{pmatrix} = \cfrac{n!}{k!(n-k)!}

Oro

n!

E

k!

Questi sono numeri fattoriali . Ricordiamo anche che un numero fattoriale si calcola moltiplicando tutti i numeri interi positivi di 1 per detto numero:

n! = 1 \cdot 2 \cdot 3 \cdots (n-1) \cdot n

Ad esempio, troveremo un numero combinatorio in modo da poter vedere come è fatto:

\begin{pmatrix} 4\\ 3 \end{pmatrix} = \cfrac{4!}{3!(4-3)!}=\cfrac{4!}{3!\cdot 1!}= \cfrac{1 \cdot 2\cdot 3 \cdot 4}{(1 \cdot 2\cdot 3) \cdot 1} = \cfrac{24}{6} = 4

I numeri combinatori possono essere determinati anche tramite la calcolatrice con il tasto

\boxed{nCr}.

Esempi di binomi di Newton

Ora che sappiamo cos’è il teorema binomiale, vediamo come applicare la formula binomiale di Newton utilizzando due esempi numerici.

Esempio 1

  • Applica il binomio di Newton per calcolare la potenza del seguente binomio:

(x+3)^2

Ovviamente, poiché questo binomio è quadrato, potrebbe essere risolto anche con le formule per le identità notevoli ( come risolvere le identità notevoli ), ma lo calcoleremo con il teorema del binomio come esempio.

Innanzitutto dobbiamo applicare la formula binomiale di Newton:

\left( a+b\right)^n =\begin{pmatrix} n \\ 0 \end{pmatrix} \right)a^n b^0 + \begin{pmatrix} n \\ 1 \end{pmatrix} a^{n-1}b^{1} + \begin{pmatrix} n \\ 2 \end{pmatrix} a^{n-2}b^{2} + \dots + \begin{pmatrix} n \\ n \end{pmatrix} a^0 b^{n}

In questo caso n=2, quindi:

\left( x+3\right)^2 =\begin{pmatrix} 2 \\ 0 \end{pmatrix} \right)x^2 \cdot 3^0 + \begin{pmatrix} 2 \\ 1 \end{pmatrix} x^1\cdot3^1 + \begin{pmatrix} 2 \\ 2 \end{pmatrix} x^{0}\cdot3^{2}

Guarda bene, all’inizio eleviamo il primo termine (x) al massimo possibile, che in questo caso è 2. Invece eleviamo il secondo termine (3) al minimo possibile, che è sempre 0. Ma man mano che ci dirigiamo a destra, dobbiamo elevare il primo termine a un numero inferiore rispetto a prima e il secondo termine a un numero superiore rispetto a prima.

Ora calcoliamo i numeri combinatori:

\left( x+3\right)^2 =1\cdot x^2\cdot 3^0 + 2\cdot x^1\cdot 3^1 + 1\cdot x^{0}\cdot 3^{2}

Risolviamo per le potenze:

\left( x+3\right)^2 =1\cdot x^2\cdot 1 + 2\cdot x\cdot 3 + 1\cdot 1\cdot 9

E infine calcoliamo le moltiplicazioni:

\left( x+3\right)^2 =x^2 + 6x + 9

Esempio 2

Ora risolveremo un problema leggermente più difficile.

  • Applica la formula binomiale di Newton per trovare la potenza del seguente binomio:

(2x+1)^3

La formula per il teorema binomiale è:

\left( a+b\right)^n =\begin{pmatrix} n \\ 0 \end{pmatrix} \right)a^n b^0 + \begin{pmatrix} n \\ 1 \end{pmatrix} a^{n-1}b^{1} + \begin{pmatrix} n \\ 2 \end{pmatrix} a^{n-2}b^{2} + \dots + \begin{pmatrix} n \\ n \end{pmatrix} a^0 b^{n}

In questo caso n=3, quindi:

\left( 2x+1\right)^3 =\begin{pmatrix} 3 \\ 0 \end{pmatrix} \right)(2x)^3 \cdot 1^0 + \begin{pmatrix} 3 \\ 1 \end{pmatrix} (2x)^{2}\cdot 1^1 + \begin{pmatrix} 3 \\ 2 \end{pmatrix} (2x)^{1}\cdot 1^{2} + \begin{pmatrix} 3 \\ 3 \end{pmatrix} (2x)^{0}\cdot 1^{3}

Calcoliamo i numeri combinatori:

\left( 2x+1\right)^3 =1\cdot (2x)^3 \cdot 1^0 + 3\cdot (2x)^{2}\cdot 1^1 + 3 \cdot (2x)^{1}\cdot 1^{2} + 1\cdot (2x)^{0}\cdot 1^{3}

Ora risolviamo le potenze, per questo è importante ricordare le seguenti due proprietà:

• Quando un monomio viene elevato ad un esponente, il coefficiente e la variabile vengono elevati allo stesso esponente →

(2x)^3=2^3\cdot x^3 =8\cdot x^3 =8x^3

• Qualsiasi termine portato a 0 dà 1 →

(2x)^0=1

Troviamo quindi le potenze attraverso queste 2 proprietà:

\left( 2x+1\right)^3 =1\cdot 2^3x^3 \cdot 1 + 3\cdot 2^2x^{2}\cdot 1 + 3 \cdot 2^1x^{1}\cdot 1 + 1\cdot 1\cdot 1

\left( 2x+1\right)^3 =1\cdot 8x^3 \cdot 1 + 3\cdot 4x^{2}\cdot 1 + 3 \cdot 2x\cdot 1 + 1\cdot 1\cdot 1

E infine moltiplichiamo i termini:

\left( 2x+1\right)^3 =8x^3 + 12x^{2}+6x + 1

Binomio di Newton e triangolo di Tartaglia (o di Pascal).

Come hai visto negli esempi sopra, il calcolo dei numeri combinatori è un po’ noioso. Per questo ti insegneremo un trucco per non dover risolvere i numeri combinatori, dato che potrai scoprire direttamente quanto valgono utilizzando il triangolo di Tartaglia, detto anche triangolo di Pascal.

Nel caso non sapessi di cosa si tratta, il triangolo di Tartaglia , chiamato anche triangolo di Pascal , è una rappresentazione matematica di numeri disposti a forma di triangolo.

Per costruire il triangolo di Tartaglia o Pascal, dobbiamo iniziare dal vertice del triangolo, che è sempre un 1, e poi determinare i numeri delle linee sottostanti. Ogni numero nelle righe successive è uguale alla somma dei due numeri immediatamente sopra di esso, ad eccezione delle estremità delle righe che sono sempre 1.

Newton accoppia 1 scuola superiore online

Quindi, ciascuno di questi numeri nel triangolo di Tartaglia corrisponde al risultato di un numero combinatorio, guarda la figura seguente:

Ad esempio, il coefficiente binomiale

\begin{pmatrix} 3 \\ 1 \end{pmatrix}

equivale a 3, perché nel triangolo di Tartaglia c’è un 3 nella sua posizione.

Possiamo quindi utilizzare il triangolo di Tartaglia (o di Pascal) per risolvere il binomio di Newton molto più velocemente, poiché ci risparmia il calcolo dei numeri combinatori.

Ad esempio, se vogliamo eseguire il seguente potenziamento di un binomio:

(x+5)^3

Applicando la regola del binomio di Newton otteniamo la seguente espressione algebrica:

\left(x+5\right)^3 =\begin{pmatrix} 3 \\ 0 \end{pmatrix} \right)x^3 \cdot 5^0 + \begin{pmatrix} 3 \\ 1 \end{pmatrix} x^{2}\cdot 5^1 + \begin{pmatrix} 3 \\ 2 \end{pmatrix} x^{1}\cdot 5^{2} + \begin{pmatrix} 3 \\ 3 \end{pmatrix} x^{0}\cdot 5^{3}

Ebbene, invece di calcolare i numeri combinatori uno per uno, possiamo semplicemente sostituire ogni numero combinatorio con il suo corrispondente coefficiente del triangolo di Tartaglia. In questo caso il binomio è elevato al 3°, corrisponde quindi al terzo livello del triangolo:

Tartaglia o triangolo di Pascal e binomio di Newton

\left(x+5\right)^3 =\color{red} \bm{1} \color{black} \cdot x^3 \cdot 5^0 + \color{red} \bm{3} \color{black} \cdot x^{2}\cdot 5^1 + \color{red} \bm{3} \color{black} \cdot x^{1}\cdot 5^{2} +\color{red} \bm{1} \color{black} \cdot x^{0}\cdot 5^{3}

E ora non ci resta che svolgere le restanti operazioni:

\left(x+5\right)^3 =1 \cdot x^3 \cdot 1 + 3\cdot x^{2}\cdot 5 + 3 \cdot x\cdot 25 +1\cdot 1\cdot 125

\left(x+5\right)^3 =x^3+ 15x^2 + 75x +125

Come puoi vedere, il triangolo di Tartaglia (o di Pascal) viene utilizzato per calcolare il binomio di Newton in modo più semplice e veloce, come abbiamo mostrato. Per questo motivo ne consigliamo l’utilizzo.

Per riassumere tutto quello che abbiamo visto finora vi lasciamo con un’immagine che mostra come appaiono le espressioni dei binomi di Newton con i numeri del triangolo di Tartaglia (o Pascal):

Binomio di Newton e triangolo di Pascal o Tartaglia

Binomio di Newton negativo: potenza di sottrazione

Finora tutti gli esempi del binomio di Newton che abbiamo risolto sono addizioni. Quando invece uno dei due termini del binomio ha segno negativo la procedura rimane simile ma cambia leggermente.

Quando uno dei termini del binomio è negativo, cioè è una sottrazione del tipo (ab) n , i segni dell’espansione del binomio di Newton devono alternarsi nella forma + – + – + – + – …

Di seguito abbiamo sviluppato le potenze dei binomi negativi dei primi 5 gradi con il teorema del binomio e con i coefficienti del triangolo di Tartaglia già in atto, in modo che tu possa trovare direttamente l’espressione binomiale che ti serve:

Potenza binomiale negativa di Newton di una sottrazione 2

Proprietà del binomio di Newton

Le espressioni binomiali di Newton hanno le seguenti caratteristiche:

  • La scomposizione del binomio di Newton dà sempre come risultato un termine in più rispetto al grado del binomio. O in altre parole, per la coppia

    (a+b)^n

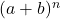
    sono colpiti

    n+1

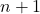
    termini.

  • I poteri dell’elemento

    a

    Iniziare con

    n

    e diminuiscono fino a raggiungere lo 0 nell’ultimo trimestre.

  • I poteri dell’elemento

    b

    vanno nella direzione opposta: iniziano da 0 e aumentano fino a raggiungere

    n

    nell’ultimo termine.

  • Per ogni elemento del binomio di Newton, la somma degli esponenti di

    a

    E

    b

    è uguale a

    n.

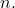
  • Il coefficiente del primo termine dell’espressione binomiale di Newton è sempre 1 (positivo) e il secondo coefficiente è equivalente all’esponente del binomio (positivo o negativo).

Calcola il kesimo termine del binomio di Newton

Sebbene ciò sia insolito, a volte possiamo incontrare problemi in cui, invece di eseguire l’espansione binomiale di Newton, ci viene chiesto di determinare il termine k-esimo del binomio di Newton, cioè il termine che occupa la posizione k.

Quindi, per calcolare il termine che occupa il posto k nel binomio di Newton, dobbiamo utilizzare una formula, che dipende dal fatto che il binomio sia un’addizione o una sottrazione:

  • Se il binomio di Newton è positivo, il valore del termine k-esimo si calcola con la seguente formula:

(a+b)^n \quad \color{red} \bm{\longrightarrow} \color{black} \quad T_k = \begin{pmatrix} n \\ k-1 \end{pmatrix} a^{n-k+1}b^{k-1}

  • Se il binomio di Newton è negativo, il valore del termine k-esimo si determina con la seguente formula:

(a-b)^n \quad \color{red} \bm{\longrightarrow} \color{black} \quad T_k = (-1)^{k-1} \begin{pmatrix} n \\ k-1 \end{pmatrix} a^{n-k+1} b^{k-1}

Ad esempio, troveremo il quarto termine del seguente binomio di grado 5:

(x+3)^5

Trattandosi di un binomio composto da una somma, applichiamo la prima formula:

T_k = \begin{pmatrix} n \\ k-1 \end{pmatrix} a^{n-k+1}b^{k-1}

Sostituiamo le variabili nella formula con i loro valori corrispondenti:

T_4 = \begin{pmatrix} 5 \\ 4-1 \end{pmatrix} x^{5-4+1}\cdot 3^{4-1}

E facciamo le operazioni:

T_4 = \begin{pmatrix} 5 \\ 3 \end{pmatrix} x^{2}\cdot 3^{3}

T_4 = 10 \cdot x^{2}\cdot 27

T_4 = 270 x^{2}

E in questo modo abbiamo calcolato il quarto termine dell’espansione binomiale di Newton senza bisogno di calcolare tutti gli altri termini.

Esercizi risolti per il binomio di Newton

Ora che abbiamo spiegato cos’è il teorema del binomio, ti lasciamo con diversi esercizi risolti passo dopo passo sul binomio di Newton in modo che tu possa esercitarti. Ricorda inoltre che puoi lasciarci qualsiasi domanda o suggerimento nei commenti.

Esercizio 1

Espandi la seguente potenza binomiale usando il teorema binomiale:

(x+4)^3

Usiamo innanzitutto la formula binomiale di Newton:

\left(x+4\right)^3 =\begin{pmatrix} 3 \\ 0 \end{pmatrix} x^3 \cdot 4^0 + \begin{pmatrix} 3 \\ 1 \end{pmatrix} x^{2}\cdot 4^1 + \begin{pmatrix} 3 \\ 2 \end{pmatrix} x^{1}\cdot 4^{2} + \begin{pmatrix} 3 \\ 3 \end{pmatrix} x^{0}\cdot 4^{3}

Poiché il binomio è elevato alla potenza di 3, guardiamo il terzo livello del triangolo di Tartaglia per trovare direttamente i numeri combinatori:

Esercizi sul teorema del binomio di Newton risolti passo passo 1 liceo

(x+4)^3 = 1\cdot x^3 \cdot 4^0+3 \cdot x^2 \cdot 4^1 + 3 \cdot x^1 \cdot 4^2+1 \cdot x^0 \cdot 4^3

Eseguiamo i poteri:

1\cdot x^3 \cdot 1 + 3 \cdot x^2 \cdot 4+ 3 \cdot x \cdot 16 +1 \cdot 1 \cdot 64

E infine moltiplichiamo:

x^3 + 3x^2 \cdot 4 + 3 x \cdot 16 + 64

\bm{x^3 + 12x^2 + 48 x + 64}

Esercizio 2

Calcola la seguente potenza con la formula binomiale di Newton:

(3x+2)^3

Per prima cosa applichiamo la formula binomiale di Newton:

\displaystyle \left(3x+2\right)^3 =\begin{pmatrix} 3 \\ 0 \end{pmatrix} (3x)^3 \cdot 2^0 + \begin{pmatrix} 3 \\ 1 \end{pmatrix} (3x)^{2}\cdot 2^1 + \begin{pmatrix} 3 \\ 2 \end{pmatrix} (3x)^{1}\cdot 2^{2} + \begin{pmatrix} 3 \\ 3 \end{pmatrix} (3x)^{0}\cdot 2^{3}

Poiché il binomio è al cubo, guardiamo il terzo livello del triangolo di Pascal per conoscere direttamente i valori dei numeri combinatori:

Esercizi sul teorema del binomio di Newton risolti passo passo 1 liceo

\left(3x+2\right)^3 = 1\cdot (3x)^3 \cdot 2^0+3 \cdot (3x)^2 \cdot 2^1+ 3 \cdot (3x)^1 \cdot 2^2+1 \cdot (3x)^0 \cdot 2^3

Calcoliamo le potenze dei monomi:

1\cdot 27x^3 \cdot 1+ 3 \cdot 9x^2 \cdot 2+3 \cdot 3x \cdot 4 + 1 \cdot 1 \cdot 8

E infine facciamo le moltiplicazioni:

27x^3 + 27x^2 \cdot 2 +9x \cdot 4+8

\bm{27x^3 + 54x^2 +36x+8}

Esercizio 3

Espandi la seguente espressione polinomiale utilizzando la formula binomiale di Newton:

(2x-2)^3

Per prima cosa utilizziamo la formula binomiale di Newton. Ma poiché abbiamo una sottrazione all’interno delle parentesi, dobbiamo alternare i segni dei coefficienti di ciascun termine:

(2x-2)^3=\begin{pmatrix} 3 \\ 0 \end{pmatrix} (2x)^3 \cdot 2^0-\begin{pmatrix} 3 \\ 1 \end{pmatrix} (2x)^2 \cdot 2^1 + \begin{pmatrix} 3 \\ 2 \end{pmatrix} (2x)^1 \cdot 2^2-\begin{pmatrix} 3 \\ 3 \end{pmatrix} (2x)^0 \cdot 2^3

Poiché il binomio è elevato alla potenza di tre, guardiamo il terzo livello del triangolo di Tartaglia per calcolare direttamente i numeri combinatori:

Esercizi sul teorema del binomio di Newton risolti passo passo 1 liceo

(2x-2)^3=1\cdot (2x)^3 \cdot 2^0-3 \cdot (2x)^2 \cdot 2^1 + 3 \cdot (2x)^1 \cdot 2^2-1 \cdot (2x)^0 \cdot 2^3

Eseguiamo i poteri:

1\cdot 8x^3 \cdot 1- 3 \cdot 4 x^2 \cdot 2+ 3 \cdot 2x \cdot 4-1 \cdot 1 \cdot 8

E risolviamo le moltiplicazioni:

8x^3 - 12 x^2 \cdot 2 +6x \cdot 4 -8

\bm{8x^3 -24 x^2 +24x -8}

Esercizio 4

Trova l’espressione estesa del seguente binomio di Newton con la formula:

(4x-3y)^4

Dobbiamo applicare la formula generale del binomio di Newton, ma poiché in questo caso abbiamo una sottrazione tra parentesi, dobbiamo alternare i segni di ciascun termine:

\begin{aligned}(4x-3y)^4 = & \begin{pmatrix} 4 \\ 0 \end{pmatrix} (4x)^4 \cdot (3y)^0-\begin{pmatrix} 4 \\ 1 \end{pmatrix} (4x)^3 \cdot (3y)^1+\begin{pmatrix} 4 \\ 2 \end{pmatrix} \cdot (4x)^2 \cdot (3y)^2 - \\[2ex] & - \begin{pmatrix} 4 \\ 3 \end{pmatrix}(4x)^1 \cdot (3y)^3+\begin{pmatrix} 4 \\ 4 \end{pmatrix} (4x)^0 \cdot (3y)^4 \end{aligned}

Poiché il binomio è elevato alla quarta, guardiamo al livello 4 del triangolo di Tartaglia per trovare direttamente i numeri combinatori:

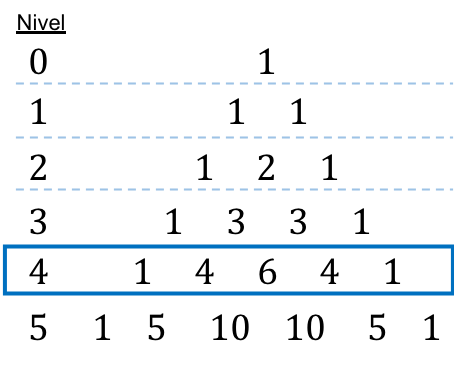
Piramide binomiale di Newton

\begin{aligned}(4x-3y)^4= & \ 1\cdot (4x)^4 \cdot (3y)^0-4\cdot (4x)^3 \cdot (3y)^1+6 \cdot (4x)^2 \cdot (3y)^2 - \\[2ex] & - 4 \cdot (4x)^1 \cdot (3y)^3+1 \cdot (4x)^0 \cdot (3y)^4 \end{aligned}

Realizziamo tutti i poteri:

1\cdot 256x^4 \cdot 1-4\cdot 64x^3 \cdot 3y+6 \cdot 16x^2 \cdot 9y^2 - 4 \cdot 4x \cdot 27y^3+1 \cdot 1 \cdot 81y^4

E, infine, risolviamo le moltiplicazioni:

256x^4-256x^3 \cdot 3y+96x^2 \cdot 9y^2 - 16x \cdot 27y^3+81y^4

\bm{256x^4-768x^3y+864x^2y^2-432xy^3+81y^4}

Esercizio 5

Determinare il settimo termine nello sviluppo della seguente espressione binomiale:

(2x-5y)^{10}

Trattandosi di un binomio negativo, dobbiamo utilizzare la seguente formula:

T_k = (-1)^{k-1} \begin{pmatrix} n \\ k-1 \end{pmatrix} a^{n-k+1} b^{k-1}

Vogliamo determinare il termine 7 e si eleva il binomio alla potenza di 10, quindi sostituendo i valori nella formula diventa:

T_7= (-1)^{7-1} \begin{pmatrix} 10 \\ 7-1 \end{pmatrix} (2x)^{10-7+1} \cdot (5y)^{7-1}

Basta quindi operare per conoscere il termine:

\begin{aligned} T_7 & = (-1)^{6} \begin{pmatrix} 10 \\ 6 \end{pmatrix} (2x)^{4} \cdot (5y)^{6} \\[2ex] & = 1 \cdot 210\cdot 16x^4 \cdot 15625y^6 \\[2ex] & = \bm{52500000x^4y^6} \end{aligned}

Storia del binomio di Newton

Sebbene l’origine del teorema del binomio sia attribuita al famoso scienziato inglese Isaac Newton (1642-1727), in realtà la prima formulazione del teorema fu scoperta per la prima volta dall’ingegnere persiano Al-Karijí intorno all’anno 1000 E si scoprì addirittura che nel XIII secolo i matematici cinesi Yang Hui e Chuh Shih-Chieh conoscevano già espansioni binomiali di piccoli gradi.

Più tardi, nel XVII secolo, Newton costruì sulle basi gettate dai matematici precedenti per estendere il teorema binomiale. Usando i metodi di interpolazione ed estrapolazione del matematico John Walls e i concetti di esponente generalizzato, riuscì a trasformare un’espressione polinomiale in una serie infinita.

Intorno al 1665 Newton riuscì a dimostrare che l’esponente n del teorema binomiale può essere anche un esponente razionale, vale a dire che la potenza di un binomio può essere risolta anche se l’esponente è una frazione. D’altronde ciò è stato dimostrato anche nel caso di esponente negativo. E, sorprendentemente, ha scoperto che gli sviluppi delle due espressioni sono serie infinite di termini.

Fu con questa scoperta che Newton cominciò a mettere in discussione la relazione tra serie infinite ed espressioni polinomiali finite, e dedusse che matematicamente le operazioni possono essere eseguite con serie infinite allo stesso modo delle espressioni polinomiali finite. Sebbene Newton non pubblicò mai questo teorema, John Walls alla fine lo fece nel 1685, attribuendo a Newton questa scoperta.

Lascia un commento

Il tuo indirizzo email non sarà pubblicato. I campi obbligatori sono contrassegnati *

Torna in alto