Come fattorizzare i polinomi (fattorizzazione polinomiale) -

In questa pagina spieghiamo come fattorizzare qualsiasi tipo di polinomio. Vedremo prima come fattorizzare un polinomio con la regola di Ruffini, poi passeremo a come si fattorizzano i polinomi senza termine indipendente, quindi analizzeremo le fattorizzazioni dei polinomi radice con frazioni e, infine, i casi particolari di fattorizzazioni (notevoli identità, fattorizzazione per raggruppamenti, trinomi, ecc.). Tutte le spiegazioni sono fatte con esempi e, inoltre, alla fine potrai esercitarti con gli esercizi risolti passo dopo passo per fattorizzare i polinomi.

Cos’è la fattorizzazione polinomiale?

La fattorizzazione polinomiale è una tecnica utilizzata in matematica per scomporre un polinomio nel prodotto di fattori.

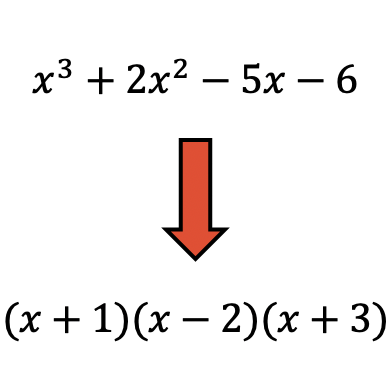
fattorizzazione dei polinomi (fattorizzazione dei polinomi)

La fattorizzazione dei polinomi è molto utile perché è più semplice eseguire operazioni con i polinomi fattorizzati.

Ora che sappiamo cos’è la fattorizzazione polinomiale, vediamo come vengono fattorizzati i polinomi.

Come fattorizzare i polinomi con la regola di Ruffini

Ovviamente, per capire come scomporre un polinomio con la regola di Ruffini, bisogna prima saper applicare la regola di Ruffini . Quindi ti lasciamo questo link nel caso in cui desideri prima rivedere come appariva la procedura.

Per fattorizzare un polinomio è necessario seguire i seguenti passaggi:

Le radici del polinomio si calcolano secondo la regola di Ruffini.
Ogni radice trovata di tipo x=a è espressa sotto forma di un fattore (xa).
Il polinomio fattorizzato è il prodotto di tutti i fattori trovati moltiplicato per il coefficiente del termine di grado più alto del polinomio non ponderato.

Affinché tu possa vedere come si fa e comprendere meglio la procedura per fattorizzare i polinomi, di seguito troverai un esempio concreto spiegato passo dopo passo:

Fattorizza il seguente polinomio:

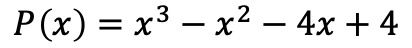
La prima cosa da fare è calcolare le radici o gli zeri del polinomio. Per fare ciò dobbiamo trovare i divisori del termine indipendente del polinomio , che in questo caso sono ±1, ±2 e ±4.

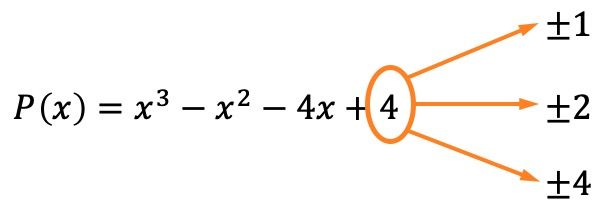
Ora sappiamo, grazie al teorema del resto e dei fattori, che se il resto della divisione del polinomio per uno di questi valori è uguale a 0, ciò significa che detto valore è una radice del polinomio.

Dobbiamo quindi dividere il polinomio per ciascuno dei divisori del termine indipendente con la regola di Ruffini e vedere in quali casi il resto è zero.

Ad esempio, iniziamo applicando la regola di Ruffini con

$x=+1:$

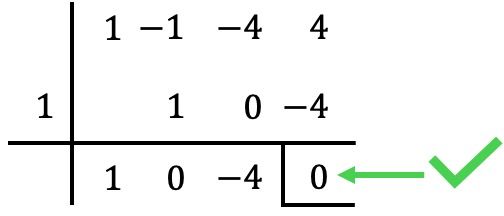
In questo caso, il resto (o residuo) della divisione è zero, quindi

$x=1$

È una radice del polinomio. ✅

Perfetto, abbiamo già una radice del polinomio, non resta che determinare le altre radici rimanenti. Per fare ciò utilizziamo, ad esempio, la regola di Ruffini con un altro divisore del termine indipendente

$x=-1.$

Inoltre, non è necessario utilizzare il metodo di Ruffini con il polinomio intero, ma possiamo continuare da dove avevamo interrotto nel passaggio precedente:

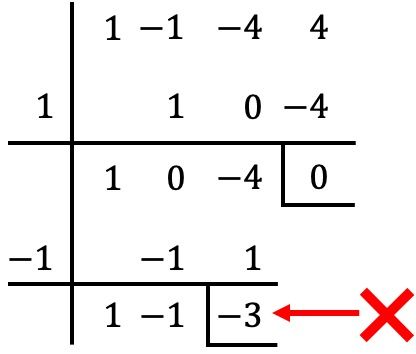
Tuttavia, in questo caso, quando si divide per

$x=-1$

il resto ottenuto è diverso da 0, quindi

$x=-1$

Non è una radice del polinomio. ❌

Dobbiamo quindi provare un altro valore, con cui ad esempio facciamo la regola Ruffini

$x=+2:$

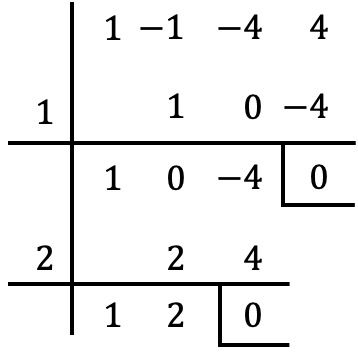
Anche in questo caso otteniamo un resto pari a zero

$x=2$

È anche una radice del polinomio.

E continuiamo ad applicare la stessa procedura. Ora controlliamo se

$x=-2$

è una radice del polinomio o no:

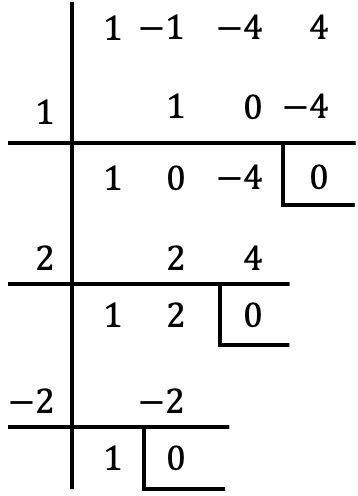
Dividendo per

$x=-2$

Con la regola di Ruffini otteniamo resto zero, quindi

$x=-2$

è una radice o zero del polinomio.

Non possiamo quindi più continuare ad applicare la regola di Ruffini, abbiamo quindi già trovato tutte le radici del polinomio, che sono:

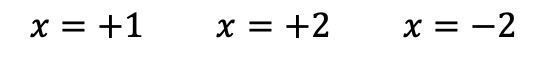
Una volta determinate tutte le radici del polinomio, possiamo fattorizzarlo. Per fare ciò, esprimi semplicemente ciascuna radice

$x=a$

sotto forma di un fattore del tipo

$(x-a)$

, vale a dire che per ogni radice bisogna mettere una parentesi con a

$x$

e la radice ha cambiato segno:

E ora che abbiamo tutte le radici espresse come fattori, dobbiamo moltiplicare tutte le parentesi per il coefficiente del termine di grado più alto del polinomio originale:

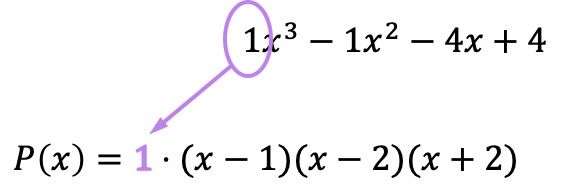
polinomi fattoriali coefficiente di grado più alto

Anche se in questo caso il coefficiente è 1 e quindi non influisce sul risultato, è importante ricordarsi di effettuare questa moltiplicazione. Poiché se detto coefficiente fosse diverso da 1, il polinomio fattorizzato cambierebbe e, quindi, non inserendo il numero commetteremmo un errore nella fattorizzazione del polinomio.

In breve, il polinomio fattorizzato è:

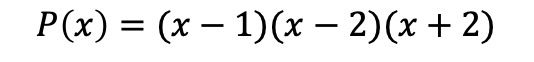
Fattorizzazione di polinomi senza termine indipendente

Abbiamo appena visto che il termine indipendente è importante per la fattorizzazione dei polinomi, poiché permette di individuare le possibili radici del polinomio. Tuttavia, come si fattorizza un polinomio che non ha termini indipendenti?

Per fattorizzare un polinomio senza termine indipendente , bisogna prima estrarre il fattore comune del polinomio, poi estrarre le radici del polinomio senza il fattore comune utilizzando la regola di Ruffini.

Scritto così potrebbe sembrare un po’ complicato, quindi risolviamo un esempio passo dopo passo così potrai vedere come fattorizzare un polinomio con un fattore comune:

Esegui la scomposizione fattoriale del seguente polinomio:

$P(x) = x^4-3x^3-x^2+3x$

Come puoi vedere, il polinomio nel problema non ha un termine indipendente, quindi dobbiamo prendere il fattore comune del polinomio. Se osserviamo attentamente, tutti gli elementi del polinomio ne hanno almeno uno

$x,$

quindi il fattore comune è

$x.$

Pertanto, estraendo il fattore comune dal polinomio, si ottiene la seguente espressione:

$P(x) = x\left(x^3-3x^2-x+3\right)$

E una volta estratto il fattore comune del polinomio, applichiamo la regola di Ruffini per calcolare le radici del polinomio raggruppate tra parentesi (con il procedimento che abbiamo visto nella sezione precedente):

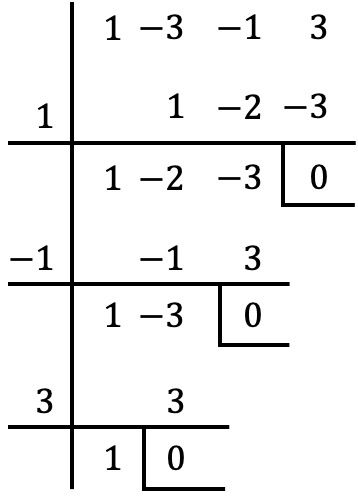
Polinomi fattoriali senza termine indipendente

Quindi le radici o gli zeri del polinomio tra parentesi sono:

$\bm{x=+1 \qquad x=-1 \qquad x=+3}$

Pertanto, per fattorizzare il polinomio, è sufficiente sostituire il polinomio tra parentesi con le sue radici sotto forma di fattore (come spiegato nella sezione precedente):

$\begin{array}{c}P(x) = x\left(x^3-3x^2-x+3\right) \\[2ex]\color{red} \bm{\downarrow} \\[2ex] \bm{P(x) = x(x-1)(x+1)(x-3)}\end{array}$

E in questo modo abbiamo già scomposto in fattori il polinomio che non aveva un termine di grado 0. Si noti che l’unica differenza è che dobbiamo prima estrarre un fattore comune, ma tutti i passaggi successivi sono esattamente gli stessi.

D’altronde questo dovresti saperlo

$x=0$

È anche una radice del polinomio, poiché quando estraiamo il fattore comune, implica che una delle radici del polinomio sia

$x=0.$

Quindi, tutte le radici del polinomio sono le seguenti:

$\bm{x= 0 \qquad x=+1 \qquad x=-1 \qquad x=+3}$

Infatti il polinomio deve avere tante radici quante ne indica il grado. In questo caso il polinomio è di grado 4 e quindi ha 4 radici.

Fattorizzazione di polinomi con radici razionali

Finora abbiamo visto esempi di fattorizzazione di polinomi con radici intere, tuttavia un polinomio può anche avere radici razionali, cioè con frazioni. Vediamo come si risolve questo tipo di fattorizzazioni polinomiali con un esempio:

Fattorizza il seguente polinomio incompleto:

$P(x) = 4x^3-7x+3$

Usiamo come sempre la regola di Ruffini con i divisori del termine indipendente per cercare di determinare le radici del polinomio:

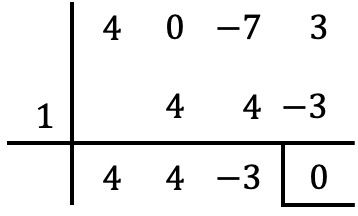
Fattorizzazione di polinomi con radici razionali

Ma non possiamo calcolare più radici con Ruffini, perché se proviamo a fare Ruffini con tutti gli altri numeri divisori del termine indipendente otteniamo un resto diverso da zero.

Ci troviamo quindi in una situazione in cui è solo con

$x=1$

il resto della divisione equivale a 0, ciò significa che il polinomio può avere radici frazionarie. Per determinare queste radici potremmo applicare Ruffini con le frazioni, tuttavia è molto facile commettere errori nei calcoli ed è per questo che in questi casi solitamente si procede così:

Quando non possiamo continuare ad applicare la regola di Ruffini con radici intere, dobbiamo porre uguale a 0 l’ultimo polinomio ottenuto e risolvere l’equazione risultante. Quindi le radici del polinomio saranno i valori trovati dall’equazione.

Se invece l’equazione non ha soluzione, significa che il polinomio non ha più radici e, quindi, non può essere completamente scomposto.

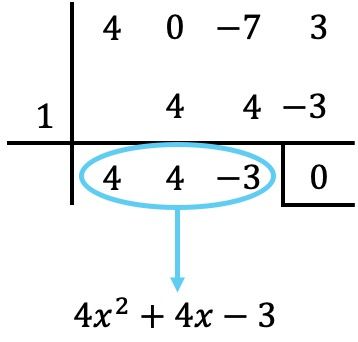
Poniamo quindi pari a zero il polinomio quoziente:

$4x^2+4x-3=0$

E usiamo la formula dell’equazione quadratica per risolvere l’equazione risultante:

$x= \cfrac{-b \pm \sqrt{b^2-4ac}}{2a}$

$x= \cfrac{-4 \pm \sqrt{4^2-4\cdot 4\cdot (-3)}}{2\cdot 4}= \cfrac{-4\pm \sqrt{16+48}}{8} = \cfrac{-4 \pm\sqrt{64}}{8}$

$\displaystyle x = \cfrac{-4 \pm 8}{8} = \begin{cases} \cfrac{-4+8}{8} = \cfrac{4}{8} = \cfrac{1}{2} \\[4ex]\cfrac{-4-8}{8} = \cfrac{-12}{8} = -\cfrac{3}{2} \end{cases}$

Le radici del polinomio sono quindi:

$x=+1 \qquad x=\cfrac{1}{2} \qquad x=-\cfrac{3}{2}$

Il polinomio ha quindi radici sotto forma di frazioni.

E una volta che conosciamo tutte le radici del polinomio, possiamo facilmente trovare il polinomio fattorizzato esprimendo ciascuna radice

$x=a$

sotto forma di un fattore del tipo

$(x-a)$

, vale a dire che per ogni radice bisogna mettere una parentesi con a

$x$

e la radice ha cambiato segno:

$\displaystyle P(x)= 4\left(x-1\right)\left(x-\frac{1}{2}\right)\left(x+\frac{3}{2}\right)$

Ricorda che per fattorizzare un polinomio devi anche moltiplicare i suoi fattori per il coefficiente del termine di grado più alto del polinomio non fattorizzato, che in questo caso è 4.

Casi particolari di fattorizzazione di polinomi

Normalmente per fattorizzare un polinomio si usa la regola di Ruffini (o divisione sintetica), come spiegato sopra. Ma a seconda del polinomio del problema, a volte è possibile eseguire la fattorizzazione polinomiale più velocemente. Vedremo ciascuno di questi casi particolari di seguito.

Scomporre identità importanti

Se vediamo che un polinomio corrisponde ad un’identità notevole (o ad un prodotto notevole) è molto semplice fattorizzarlo. Tuttavia per poterlo fare devi padroneggiare leformule per le identità notevoli , altrimenti ti consiglio di dare un’occhiata a questo link dove non solo troverai le formule, ma potrai anche vedere esempi di notabili. identità e puoi anche praticare esercizi con loro risolti passo dopo passo.

Differenza di quadrati

Come ben sai, la formula per l’identità notevole della differenza dei quadrati è la seguente:

$a^2-b^2=(a+b)\cdot (a-b)$

Pertanto, se troviamo un polinomio che soddisfa l’espressione

$a^2-b^2$

possono essere presi in considerazione direttamente.

Guarda il seguente esempio in cui viene presa in considerazione la differenza di quadrati:

$x^2-9 = (x+3)(x-3)$

Le radici del polinomio invece sono:

$x=-3 \qquad x=+3$

Altri esempi di fattorizzazione di binomi che sono differenze di quadrati:

$x^2-4=(x+2)(x-2) \quad \longrightarrow \quad \text{ra\'ices: } x=-2, +2$

$x^2-16=(x+4)(x-4) \quad \longrightarrow \quad \text{ra\'ices: } x=-4, +4$

$x^2-25=(x+5)(x-5) \quad \longrightarrow \quad \text{ra\'ices: } x=-5, +5$

Quadrato di addizione e sottrazione

Dovresti già conoscere le formule per le due principali identità notevoli rimaste: il quadrato dell’addizione e il quadrato della sottrazione.

Quadrato della somma

$a^2+2ab+b^2 = (a+b)^2$

Quadrato di sottrazione

$a^2-2ab+b^2= (a-b)^2$

Quindi, se ci rendiamo conto che un polinomio corrisponde a una di queste due identità notevoli, possiamo fattorizzarlo direttamente. Guarda i seguenti esempi:

$x^2+6x+9 = (x+3)^2$

Doppia radice:

$x=-3$

$x^2-8x+16 = (x-4)^2$

Doppia radice:

$x=4$

Identificare questi tipi di prodotti importanti è un po’ più difficile. Un trucco consiste nel verificare se il termine indipendente del polinomio è il quadrato di un numero e se il termine di grado superiore è il quadrato di un monomio (di solito

$x$

), in questo caso è sufficiente verificare che sia vero

$2ab$

è pari alla fine del diploma intermedio.

Ad esempio, se abbiamo il seguente polinomio:

$x^2+10x+25$

In questo caso può essere solo il quadrato di una somma, perché tutti gli elementi del polinomio sono positivi. Quindi la variabile

$b$

della formula deve essere 5, poiché è la radice del termine indipendente, e la variabile

$a$

dev’essere

$x$

, poiché è la radice del termine may grado.

$a=\sqrt{x^2} = x$

$b=\sqrt{25} = 5$

Ora non ci resta che dimostrare che la formula del quadrato della somma è soddisfatta dal termine di grado intermedio:

$2ab = 10x \ \color{blue} \bm{?}$

$2ab = 2\cdot x \cdot 5 = 10 x$

✅

La formula per il prodotto notevole è soddisfatta, quindi il polinomio scomposto è:

$x^2+10x+25 = (x+5)^2$

E la radice di questo polinomio è

$x=-5,$

che è una radice doppia perché il suo fattore è quadrato (si ripete due volte).

Di seguito sono riportati altri esempi di fattorizzazione di trinomi quadrati perfetti:

$x^2-4x+4=(x-2)^2 \quad \longrightarrow \quad \text{ra\'iz doble: } x=+2$

$x^2+14x+49=(x+7)^2 \quad \longrightarrow \quad \text{ra\'iz doble: } x=-7$

$9x^2-12x+4=(3x-2)^2 \quad \longrightarrow \quad \text{ra\'iz doble: } x=+\cfrac{2}{3}$

Fattorizzazione dei trinomi di secondo grado

Come abbiamo appena visto, a volte ci sono trinomi che sono quadrati perfetti e questi possono essere fattorizzati direttamente con le formule per le identità notevoli. Ma la maggior parte dei trinomi non sono prodotti degni di nota, quindi come fattorizziamo questi casi di polinomi?

Per fattorizzare un polinomio quadratico non è necessario applicare il metodo Ruffini, basta porre il polinomio uguale a zero e risolvere l’equazione quadratica risultante. Le soluzioni dell’equazione saranno quindi le radici del polinomio.

Ad esempio, se ci viene chiesto di fattorizzare il seguente polinomio di grado 2:

$P(x) = x^2+2x-15$

Invece di usare Ruffini, poniamo il polinomio uguale a 0:

$x^2+2x-15=0$

E ora usiamo la formula dell’equazione di 2° grado per trovare le soluzioni dell’equazione:

$x= \cfrac{-b \pm \sqrt{b^2-4ac}}{2a}$

$x= \cfrac{-2 \pm \sqrt{2^2-4\cdot 1\cdot (-15)}}{2\cdot 1}= \cfrac{-2\pm \sqrt{4+60}}{2} = \cfrac{-2 \pm\sqrt{64}}{2}$

$\displaystyle x = \cfrac{-2 \pm 8}{2} = \begin{cases} \cfrac{-2+8}{2} = \cfrac{6}{2} = 3 \\[4ex]\cfrac{-2-8}{2} = \cfrac{-10}{2} = -5 \end{cases}$

Le radici del polinomio sono quindi:

$x=3 \qquad x=-5$

E infine, la fattorizzazione polinomiale è:

$P(x) =(x-3)(x+5)$

Fattorizzazione di trinomi di quarto grado con esponenti pari

Come nel caso precedente, per fattorizzare un polinomio di quarto grado con esponenti pari, dobbiamo porre il polinomio uguale a zero e risolvere l’equazione biquadrata. In modo che i valori trovati corrispondano alle radici del polinomio.

Ad esempio, fattorizzeremo il seguente polinomio di grado 4:

$P(x) =x^4-5x^2+4$

Per prima cosa impostiamo il polinomio uguale a zero:

$x^4-5x^2+4=0$

Ora dobbiamo risolvere l’equazione biquadrata. Per fare ciò, apportiamo una modifica alla variabile:

$x^2=t$

$t^2-5t+4=0$

Risolviamo l’equazione quadratica con la formula:

$t= \cfrac{-b \pm \sqrt{b^2-4ac}}{2a}$

$t= \cfrac{-(-5) \pm \sqrt{(-5)^2-4\cdot 1\cdot 4}}{2\cdot 1}= \cfrac{5\pm \sqrt{25-16}}{2} = \cfrac{5 \pm\sqrt{9}}{2}$

$\displaystyle t = \cfrac{5 \pm 3}{2} = \begin{cases} \cfrac{5+3}{2} = \cfrac{8}{2} = 4 \\[4ex]\cfrac{5-3}{2} = \cfrac{2}{2} = 1 \end{cases}$

Annulliamo il cambio di variabile per calcolare le radici:

$x^2=t$

$x^2=4$

$x=\sqrt{4}$

$x=\pm 2$

$x^2=1$

$x=\sqrt{1}$

$x=\pm 1$

Le radici del polinomio sono quindi:

$x=+2 \qquad x=-2 \qquad x=+1 \qquad x=-1$

E una volta che conosciamo le radici o gli zeri del polinomio, lo fattorizziamo esprimendo le sue radici algebricamente sotto forma di fattori:

$P(x) =(x-1)(x+1)(x-2)(x+2)$

Fattorizzare i polinomi per raggruppamento

In alcuni casi molto particolari, è possibile utilizzare una formula per fattorizzare un tipo molto particolare di polinomio.

Se abbiamo un polinomio della forma seguente:

$x^2-ax- bx+ab$

Possiamo semplificare il polinomio eliminando il fattore comune:

$x^2-ax- bx+ab = x(x-a)-b(x-a)$

E il polinomio può essere ulteriormente semplificato estraendo il fattore comune una seconda volta:

$x(x-a)-b(x-a) =(x-a)\cdot (x-b)$

In questo modo abbiamo potuto fattorizzare il polinomio senza applicare Ruffini o qualsiasi altro metodo. E le radici di detto polinomio sarebbero:

$x=a \qquad x=b$

Vediamo ora questo metodo con un esempio numerico:

$x^2-3x-2x+6$

Per prima cosa rimuoviamo il fattore comune con

$x$

e con 2:

$x^2-3x-2x+6 = x(x-3)-2(x-3)$

E come adesso

$(x-3)$

è un fattore comune del polinomio, estraiamo il fattore comune di

$(x-3):$

$x(x-3)-2(x-3)=(x-3)\cdot (x-2)$

Le radici del polinomio sono quindi:

$x=3 \qquad x=2$

Questo metodo è anche chiamato fattorizzazione dei polinomi mediante estrazione del doppio fattore comune. Nonostante si tratti di una procedura molto rapida, sconsigliamo di eseguire questo tipo di fattorizzazione perché quando si fattorizza con questo metodo vengono frequentemente segnalati errori. Inoltre, come abbiamo visto sopra, un polinomio di grado 2 può anche essere scomposto risolvendo una semplice equazione quadratica. Insomma, non succede nulla se non si comprende bene questo metodo.

Infine è da notare che esistono ancora altri metodi di fattorizzazione polinomiale più complessi, come l’algoritmo LLL, il metodo Kronecker e il metodo Trager, che non vengono qui spiegati a causa della loro difficoltà matematica.

Esercizi risolti sulla fattorizzazione dei polinomi

Dopo aver visto tutti i tipi di fattorizzazione dei polinomi, ti consigliamo di esercitarti provando a risolvere gli esercizi. Questo è il motivo per cui di seguito abbiamo preparato diversi esercizi risolti passo dopo passo per la fattorizzazione dei polinomi. Ricorda che se hai domande puoi scriverle nei commenti e ti risponderemo velocemente.

Esercizio 1

Esegui la fattorizzazione del seguente polinomio di grado 3:

$P(x)=x^3-3x^2-6x+8$

Vedi la soluzione

È un polinomio completo, ordinato, di terzo grado e in definitiva indipendente. Applichiamo quindi il metodo di Ruffini per determinare le radici del polinomio:

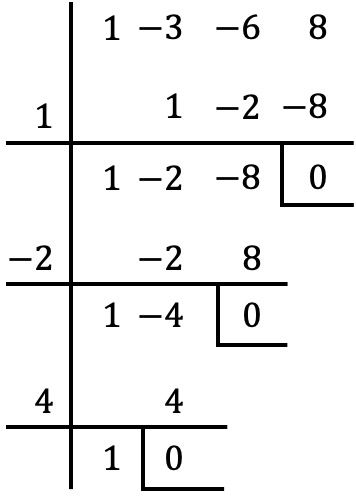
Esercizi passo passo per la fattorizzazione dei polinomi

Le radici del polinomio sono quindi le seguenti:

$x=+1 \qquad x=-2 \qquad x=+4$

La fattorizzazione polinomiale è quindi:

$P(x)= 1 \cdot (x-1)\cdot (x+2) \cdot (x-4)$

$\bm{P(x)= (x-1)(x+2)(x-4)}$

Esercizio 2

Calcolare la fattorizzazione del seguente polinomio di grado 4:

$P(x)=x^4+x^3-7x^2-x+6$

Vedi la soluzione

È un polinomio di quarto grado e con termine indipendente, utilizziamo quindi il metodo Ruffini per trovare le radici del polinomio:

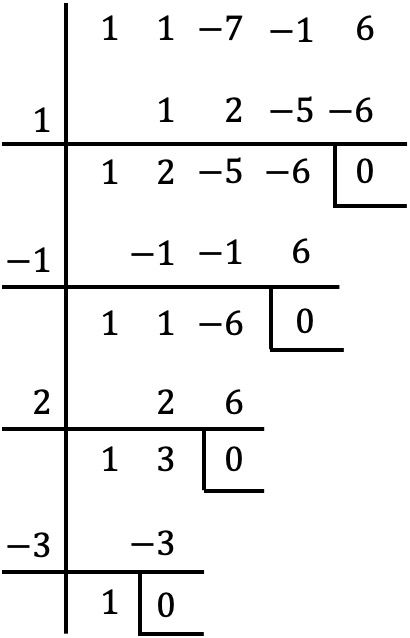
Esercizi di fattorizzazione polinomiale pdf

Le radici del polinomio sono quindi:

$x=+1 \qquad x=-1 \qquad x=2 \qquad x=-3$

E quando fattorizziamo il polinomio, ci rimane:

$P(x)= 1 \cdot (x-1)\cdot (x+1)\cdot (x-2) \cdot (x+3)$

$\bm{P(x)= (x-1)(x+1)(x-2)(x+3)}$

Esercizio 3

Trovare la fattorizzazione del seguente polinomio di quarto grado:

$P(x)=x^4-2x^3-13x^2-10x$

Vedi la soluzione

In questo caso il polinomio non ha termini indipendenti, dobbiamo prima estrarre un fattore comune:

$P(x)=x(x^3-2x^2-13x-10)$

Ora che abbiamo preso il divisore comune di x, calcoliamo le radici o gli zeri del polinomio tra parentesi utilizzando il metodo di Ruffini:

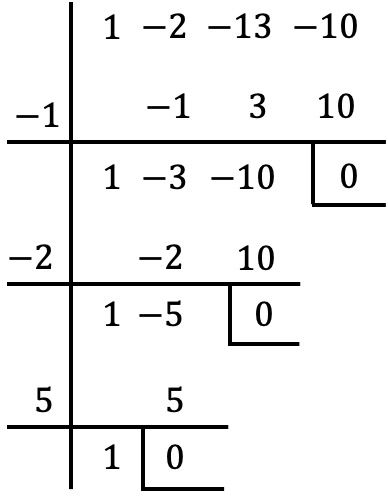
fattorizzazione dei polinomi di Ruffini esercizi risolti pdf

Quindi le radici del polinomio sono quelle che abbiamo trovato con il metodo Ruffini più x=0 del divisore comune:

$x=0 \qquad x=-1 \qquad x=-2 \qquad x=5$

Ed infine, scomponendo il polinomio in fattori otteniamo la seguente espressione:

$P(x)= 1 \cdot x \cdot (x+1)\cdot (x+2)\cdot (x-5)$

$\bm{P(x)= x(x+1)(x+2)(x-5)}$

Esercizio 4

Trasforma il seguente polinomio di terzo grado in fattori:

$P(x)=6x^3+25x^2+21x-10$

Vedi la soluzione

Questo polinomio ha un termine indipendente, calcoliamo quindi le sue radici con l’algoritmo di Ruffini:

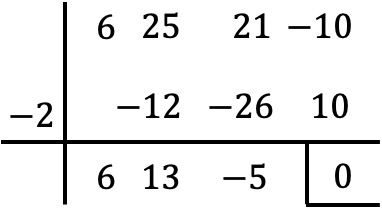
polinomi fattoriali di grado 3 nella riga 2

Tuttavia, arrivati a questo punto, non possiamo continuare ad applicare la regola di Ruffini, perché senza un altro intero il resto della divisione è zero.

Pertanto, impostiamo il polinomio risultante uguale a zero:

$6x^2+13x-5=0$

E applichiamo la formula delle equazioni quadratiche per risolvere l’equazione risultante:

$x= \cfrac{-b \pm \sqrt{b^2-4ac}}{2a}$

$x= \cfrac{-13 \pm \sqrt{13^2-4\cdot 6\cdot (-5)}}{2\cdot 6}= \cfrac{-13\pm \sqrt{169+120}}{12} = \cfrac{-13 \pm\sqrt{289}}{12}$

$\displaystyle x = \cfrac{-13 \pm 17}{12} = \begin{cases} \cfrac{-13+17}{12} = \cfrac{4}{12} = \cfrac{1}{3} \\[4ex]\cfrac{-13-17}{12} = \cfrac{-30}{12} = -\cfrac{5}{2} \end{cases}$

Le radici o zeri del polinomio sono quindi:

$x=-2 \qquad x=\cfrac{1}{3} \qquad x=-\cfrac{5}{2}$

Quindi la fattorizzazione del polinomio deve essere fatta con le frazioni:

$\displaystyle P(x)= 6\left(x+2\right)\left(x-\frac{1}{3}\right)\left(x+\frac{5}{2}\right)$

Esercizio 5

Determinare la fattorizzazione del seguente polinomio di grado 6:

$P(x)=x^6-3x^5+14x^3-12x^2$

Vedi la soluzione

Il polinomio nel problema non ha termini indipendenti, quindi dobbiamo prima estrarre il fattore comune, che in questo caso lo è

$x^2:$

$P(x)=x^2(x^4-3x^3+14x-12)$

E una volta eliminato il fattore comune dal polinomio, troviamo tra parentesi le radici del polinomio utilizzando la regola di Ruffini:

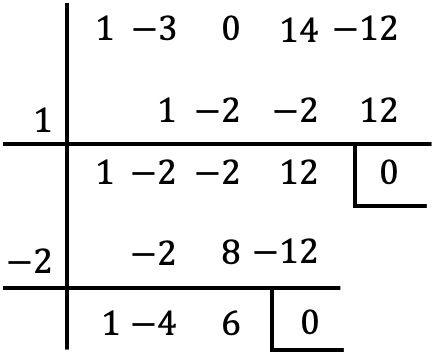
Ma quando arriviamo a questo punto, non possiamo continuare ad andare avanti, perché senza un altro numero intero, il resto è zero.

Poniamo quindi pari a zero il polinomio ottenuto:

$x^2-4x+6=0$

E risolviamo l’equazione quadratica con la formula:

$x= \cfrac{-b \pm \sqrt{b^2-4ac}}{2a}$

$x= \cfrac{-(-4) \pm \sqrt{(-4)^2-4\cdot 1\cdot 6}}{2\cdot 1}= \cfrac{4\pm \sqrt{16-24}}{2} = \cfrac{4 \pm\sqrt{-8}}{2} \ \color{red} \bm{\times}$

Non ci sono radici dei numeri negativi, quindi l’equazione non ha soluzione, il che significa che non possiamo trovare altre radici del polinomio. In altre parole, il polinomio non è completamente fattorizzabile.

Tuttavia, le radici che siamo riusciti a trovare sono:

$x=0 \qquad x=0 \qquad x=1 \qquad x=-2$

Tieni presente che la radice

$x=0$

viene ripetuto due volte perché abbiamo rimosso il fattore comune da

$x^2,$

e poiché è quadrata, ciò implica che è una radice doppia.

In conclusione il polinomio fattorizzato sarà il prodotto di tutte le radici trovate espresse come fattori

$(x-a)$

moltiplicato per il polinomio ottenuto dalla regola di Ruffini che non poteva essere ulteriormente preso in considerazione:

$P(x)= 1 \cdot x^2 \cdot (x-1)\cdot (x+2)\cdot (x^2-4x+6)$

$\bm{P(x)= x^2(x-1)(x+2)(x^2-4x+6)}$

Esercizio 6

Esegui la fattorizzazione di tutti i seguenti polinomi:

$\text{A)} \ P(x)=x^2 + 12x+36$

$\text{B)} \ Q(x)=x^2 -64$

$\text{C)} \ R(x)=x^2 - 18x+81$

$\text{D)} \ S(x)=x^2+10x+24$

Vedi la soluzione

Il polinomio della sezione A) corrisponde a un’identità notevole, in particolare al quadrato della somma. La sua fattorizzazione è quindi:

$P(x)=x^2 + 12x+36 = \bm{(x+6)^2}$

Anche il polinomio della sezione B) è un prodotto notevole, in particolare è la differenza dei quadrati, quindi:

$Q(x)=x^2 -64 = \bm{(x+8)(x-8)}$

Allo stesso modo, il polinomio della sezione C) è un’uguaglianza notevole, in particolare è costituito dal quadrato di una sottrazione. La sua fattorizzazione è quindi:

$R(x)=x^2 - 18x+81 = \bm{(x-9)^2}$

Infine, il polinomio nella parte D) non è un’identità notevole. Dobbiamo quindi porre il polinomio uguale a 0 e risolvere l’equazione risultante per trovarne le radici:

$x^2+10x+24 =0$

Usiamo la formula dell’equazione quadratica:

$x= \cfrac{-b \pm \sqrt{b^2-4ac}}{2a}$

$x= \cfrac{-10 \pm \sqrt{10^2-4\cdot 1\cdot 24}}{2\cdot 1}= \cfrac{-10\pm \sqrt{100-96}}{2} = \cfrac{-10 \pm\sqrt{4}}{2}$

$\displaystyle x = \cfrac{-10 \pm 2}{2} = \begin{cases} \cfrac{-10+2}{2} = \cfrac{-8}{2} = -4 \\[4ex]\cfrac{-10-2}{2} = \cfrac{-12}{2} = -6\end{cases}$

Le radici del polinomio D) sono quindi:

$x=-4 \qquad x=-6$

E infine, il risultato della fattorizzazione polinomiale è:

$\bm{S(x)=(x+4)(x+6)}$

Cos’è la fattorizzazione polinomiale?

Come fattorizzare i polinomi con la regola di Ruffini

Fattorizzazione di polinomi senza termine indipendente

Fattorizzazione di polinomi con radici razionali

Casi particolari di fattorizzazione di polinomi

Scomporre identità importanti

Differenza di quadrati

Quadrato di addizione e sottrazione

Fattorizzazione dei trinomi di secondo grado

Fattorizzazione di trinomi di quarto grado con esponenti pari

Fattorizzare i polinomi per raggruppamento

Esercizi risolti sulla fattorizzazione dei polinomi

Esercizio 1

Esercizio 2

Esercizio 3

Esercizio 4

Esercizio 5

Esercizio 6

Lascia un commento Annulla risposta