▷ Come rimuovere (o estrarre) il fattore comune ✅ (esercizi risolti)

In questa pagina spieghiamo come prendere (o estrarre) il fattore comune di un polinomio. Qui troverai i diversi tipi di fattore comune e potrai vedere diversi esempi di come questo viene ottenuto. Inoltre, puoi allenarti con esercizi risolti passo dopo passo.

Qual è il fattore comune?

In matematica, il fattore comune è un fattore presente in tutti i termini di un polinomio, ovvero il fattore comune è costituito da un numero o una lettera che moltiplica ciascun termine di un polinomio.

Ad esempio, identificheremo qual è il fattore comune del seguente polinomio:

$4x+4y$

Al numero 4 si ripete in tutti i termini del polinomio:

$\color{red} \bm{4} \color{black} x + \color{red} \bm{4} \color{black} y$

Il fattore comune di questo polinomio è quindi pari a 4.

$\displaystyle \text{Factor com\'un} = 4 {\phantom{\frac{1}{2}}$

Come ottenere (o estrarre) il fattore comune

Una volta conosciuto il significato di fattore comune, vediamo come ottenere il fattore comune da un polinomio.

Quando due o più termini di un polinomio hanno un fattore comune, il fattore comune può essere preso (o estratto) per trasformare addizioni o sottrazioni del polinomio in una moltiplicazione.

Potrebbe sembrare un po’ difficile da scrivere, quindi vediamo come estrarre il fattore comune da un polinomio con un esempio:

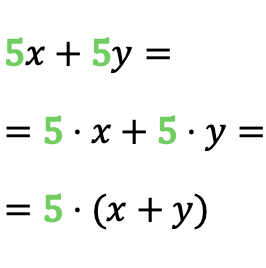
estrarre o rimuovere il fattore comune da un polinomio

Come puoi vedere nell’esempio, il numero 5 si ripete nel monomio 5x e nel monomio 5y, quindi il divisore comune del polinomio è 5. Quindi una volta individuato il divisore comune, possiamo convertire la somma dei monomi in un Prodotto.

Non dimenticare di inserire le parentesi quando estrai il fattore comune, perché il fattore comune deve moltiplicare tutti gli addendi.

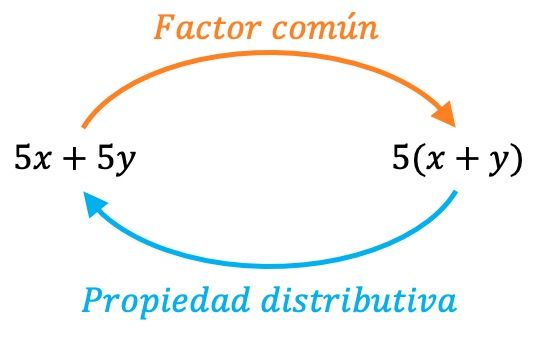
Rimuovere il fattore comune è l’operazione inversa della proprietà distributiva , cioè stiamo effettivamente applicando la proprietà distributiva al contrario. Pertanto possiamo sempre verificare di aver estratto correttamente il fattore comune eseguendo il processo inverso:

Se applicando la proprietà distributiva otteniamo fin dall’inizio lo stesso polinomio, significa che abbiamo ottenuto correttamente il fattore comune.
D’altra parte, quando il risultato dell’utilizzo della proprietà distributiva è un altro polinomio diverso dal polinomio originale, ciò implica che abbiamo commesso un errore nel processo di estrazione del fattore comune.

Esempi di assunzione (o estrazione) del fattore comune

Vi lasciamo con altri esempi per completare la comprensione del concetto di fattore comune:

Esempio 1

Come puoi vedere in questo esempio, un fattore comune può essere estratto da più di due termini contemporaneamente:

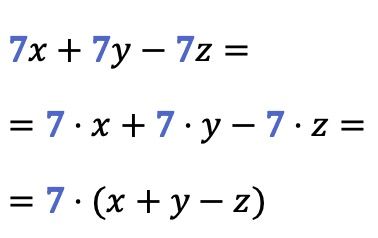
Esempio 2

Puoi anche estrarre un fattore comune dalle variabili (o lettere):

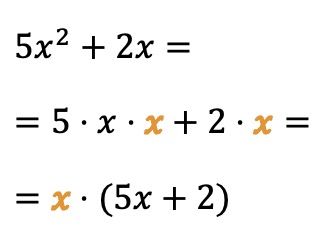
estrarre il fattore comune nelle espressioni algebriche

In questo caso la lettera x moltiplica i due termini del polinomio, quindi possiamo semplificare l’espressione algebrica prendendo la variabile x come fattore comune.

Esempio 3

In questo esempio, il primo termine ha la variabile x elevata alla potenza di 3 e nel secondo termine la x è elevata alla potenza di 2, quindi entrambi i termini hanno due x. Il divisore comune quindi non è solo x, ma x ² :

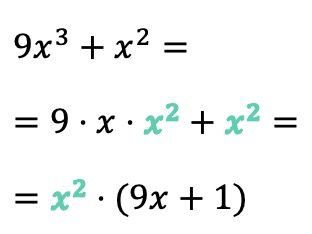
fattore comune algebrico di x al quadrato

Notiamo invece che se il fattore comune del polinomio coincide esattamente con un termine, quando estraiamo il fattore comune, al suo posto dobbiamo mettere 1 . Altrimenti, se non mettessimo nulla al suo posto, non otterremmo un’espressione equivalente.

come estrarre o trovare un fattore comune

Esempio 4

A volte il fattore comune non è così evidente e non è direttamente visibile, ma piuttosto è un divisore dei coefficienti dei monomi. Ad esempio, il fattore comune nell’esempio seguente è 3, poiché la scomposizione fattoriale di 6 e 9 contiene 3:

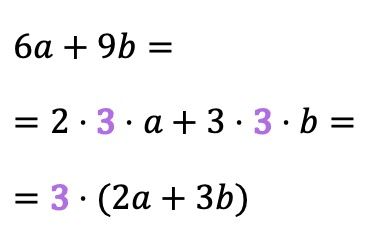
Questo tipo di fattore comune è chiamato in alcuni libri di algebra massimo fattore comune , poiché il fattore comune è allo stesso tempo il massimo comun divisore (MCD) dei coefficienti dei termini polinomiali.

Se sei arrivato fin qui, significa che probabilmente sai già come trovare il fattore comune di un polinomio perfetto. Tuttavia, non ti sei chiesto a cosa serve il fattore comune? Bene, un’applicazione del fattore comune è che viene utilizzato per fattorizzare i polinomi. Se ancora non sai di cosa si tratta, in questo link puoi vedere cos’è la fattorizzazione polinomiale e perché il fattore comune è così importante per eseguire questa operazione polinomiale.

Fattore comune per le frazioni

Il fattore comune è anche molto utile per semplificare i termini in frazioni con polinomi al numeratore e al denominatore.

Per vedere come si fa, semplifichiamo la seguente frazione come esempio:

$\cfrac{2x^2+4}{14x+8y}$

La prima cosa che dobbiamo fare è trovare il fattore comune del polinomio del numeratore e del polinomio del denominatore. In questo caso il fattore comune dei due polinomi è 2:

$\cfrac{\color{red} \bm{2} \color{black}\cdot x^2+\color{red} \bm{2} \color{black}\cdot 2 }{\color{red} \bm{2} \color{black}\cdot 7x+\color{red} \bm{2} \color{black} \cdot 4y}$

Estraiamo ora il fattore comune dei due polinomi:

$\cfrac{\color{red} \bm{2} \color{black}\left(x^2+2\right)}{\color{red} \bm{2} \color{black}\left(7x+4y\right)}$

E una volta ottenuto un fattore comune per entrambi i polinomi, dobbiamo eliminare i fattori che si ripetono al numeratore e al denominatore :

$\cfrac{\cancel{2}\left(x^2+2\right)}{ \cancel{2}\left(7x+4y\right)}$

In conclusione la frazione semplificata è:

$\cfrac{x^2+2}{7x+4y}$

Fattore comune per raggruppamento

Un modo per ridurre i termini di un polinomio è utilizzare il metodo dei fattori comuni raggruppando i termini , chiamato anche estrazione del doppio fattore comune. Come suggerisce il nome, questa procedura consiste nel semplificare l’espressione di un polinomio raggruppandone due volte i termini.

Questo metodo è un po’ complesso, quindi vediamo come si applica passo dopo passo con il seguente polinomio:

$x^2+2x+5x+10$

Dobbiamo prima determinare due diversi possibili fattori comuni, quindi separiamo il polinomio in due parti:

$(x^2+2x)+(5x+10)$

In questo caso, gli elementi x ² e 2x hanno la lettera x come fattore comune, mentre i termini 5x e 10 hanno 5 come fattore comune (poiché 10 è multiplo di 5). Quindi abbiamo questi due fattori in comune:

$(x\cdot x+2\cdot x)+(5\cdot x+5\cdot 2)$

$x(x+2)+5(x+2)$

E infine, poiché i restanti due prodotti polinomiali hanno il fattore (x+2), possiamo semplificare il polinomio come segue:

$(x+2)\cdot (x+5)$

Come puoi vedere, questo metodo non è affatto semplice. Quindi non esitare a farci qualsiasi domanda tu abbia nei commenti e ti risponderemo il prima possibile.

Esercizi sui fattori comuni risolti passo dopo passo

Ti lasciamo diversi esercizi risolti passo dopo passo in modo che tu possa esercitarti a estrarre il fattore comune da un polinomio.

Esercizio 1

Estrai il fattore comune dai seguenti polinomi:

$\text{A)} \ 6a+6b$

$\text{B)} \ 3x^2+8x$

$\text{C)} \ 2x-4$

$\text{D)} \ -5x^4+x^2$

Vedi la soluzione

A) Tutti i termini che compongono il primo polinomio hanno valore 6, quindi il divisore comune del polinomio è 6:

$6a+6b = 6\cdot a + 6 \cdot b = \bm{6\cdot (a+b)}$

B) Nel secondo polinomio tutti i suoi elementi hanno almeno una lettera x. Ecco il fattore comune del polinomio:

$3x^2+8x = 3x \cdot x+8\cdot x= \bm{x\cdot (3x+8)}$

C) Il primo monomio del polinomio ha ovviamente 2, e il secondo monomio è multiplo di 2. Quindi il fattore comune del polinomio è 2:

$2x-4= 2\cdot x - 2\cdot 2 =\bm{2\cdot (x-2)}$

D) Nell’ultimo polinomio tutte le variabili sono almeno al quadrato. Il divisore comune è quindi x ² :

$-5x^4+x^2= -5x^2\cdot x^2 +1 \cdot x^2 = \bm{x^2\cdot (-5x^2+1)}$

Ricorda che quando il divisore comune è identico a un termine, al suo posto va messo un 1.

Esercizio 2

Consideriamo il fattore comune dei seguenti polinomi:

$\text{A)} \ 8x^2 + 10y^3$

$\text{B)} \ 5x^3-2x^2+4x$

$\text{C)} \ 25x^5+15x^3-20$

$\text{D)} \ 9x^4-3x^3-21x^2-6x$

Vedi la soluzione

A) Tutti i coefficienti degli elementi che compongono il primo polinomio sono multipli di 2, quindi estraendo il fattore comune il polinomio diventa:

$\begin{array}{l} 8x^2 + 10y^3 = \\[2ex] = 2\cdot 4x^2 +2\cdot 5y^3 = \\[2ex] = \bm{2\left(4x^2+5y^3\right)} \end{array}$

B) In tutti i termini del polinomio esiste almeno una x, quindi:

$\begin{array}{l}5x^3-2x^2+4x = \\[2ex] = 5x^2\cdot x-2x\cdot x+4\cdot x= \\[2ex] =\bm{x\left(5x^2-2x+4\right)}\end{array}$

C) Il massimo comun divisore dei coefficienti di tutti i termini del polinomio è 5, per cui il massimo comun divisore di detto polinomio è 5:

$\begin{array}{l}25x^5+15x^3-20 = \\[2ex] =5\cdot 5x^5+5\cdot 3x^3-5\cdot 4 = \\[2ex] = \bm{5\left(5x^5+3x^3-4\right)}\end{array}$

D) Tutti i termini del polinomio hanno almeno una x e inoltre tutti i coefficienti sono multipli di 3. Pertanto il fattore comune del polinomio è 3x:

$\begin{array}{l}9x^4-3x^3-21x^2-6x = \\[2ex] = 3x^3\cdot 3x-x^2\cdot 3x-7x\cdot 3x-2\cdot 3x= \\[2ex] = \bm{3x\left(3x^3-x^2-7x-2 \right)}\end{array}$

Esercizio 3

Trova il fattore comune di ciascuno dei seguenti polinomi e sottrailo:

$\text{A)} \ 4a^2b^5+7a^4b^3-10a^6b^4$

$\text{B)} \ 16x^4y^7z+8x^2y^2z^2+ 24x^3y^5$

$\text{C)} \ 6ab^2c^4-6ab^2c+12a^3b^2c$

$\text{D)} \ 18x^2y+10xy-5xy^3+4z$

Vedi la soluzione

A) Tutti i monomi hanno almeno la lettera

$a$

quadrato e la lettera

$b$

al cubo, quindi il fattore comune è

$a^2b^3:$

$\begin{array}{l} 4a^2b^5+7a^4b^3-10a^6b^4 = \\[2ex] = 4b^2\cdot a^2b^3+7a^2\cdot a^2b^3-10a^4b\cdot a^2b^3 = \\[2ex] = \bm{a^2b^3\left(4b^2+7a^2-10a^4b\right)} \end{array}$

B) Tutti i coefficienti del polinomio sono multipli di 8 e inoltre hanno come parti letterali almeno x ² e y ² . Il fattore comune del polinomio è quindi 8x ² y ² .

$\begin{array}{l}16x^4y^7z+8x^2y^2z^2+ 24x^3y^5 = \\[2ex] = 2x^2y^5z \cdot 8x^2y^2 +z^2\cdot 8x^2y^2+ 3xy^3\cdot 8x^2y^2= \\[2ex] =\bm{8x^2y^2\left(2x^2y^5z+z^2+3xy^3\right)}\end{array}$

C) In questo caso il fattore comune coincide con il valore del monomio intermedio

$\left(6ab^2c\right)$

, poiché i coefficienti degli altri monomi sono multipli di

$6$

e assolutamente tutti lo hanno

$ab^2c:$

$\begin{array}{l}6ab^2c^4-6ab^2c+12a^3b^2c = \\[2ex] =c^3\cdot 6ab^2c -1\cdot 6ab^2c+2a^2 \cdot 6ab^2c = \\[2ex] = \bm{6ab^2c\left(c^3-1+2a^2\right)}\end{array}$

D) In questo caso particolare il polinomio non ha alcun fattore comune, poiché nessun fattore si ripete in tutti i termini del polinomio. Pertanto, l’espressione polinomiale non può essere semplificata algebricamente.

$18x^2y+10xy-5xy^3+4z$

Esercizio 4

Semplifica le seguenti frazioni algebriche prendendo il fattore comune:

$\text{A)} \ \cfrac{10x^2+30}{5x-20}$

$\text{B)} \ \cfrac{16x^2-8}{24x-32}$

$\text{C)} \ \cfrac{49x^3+7x}{35x^2-14}$

$\text{D)} \ \cfrac{8x^4+16x^3-4x^2}{12x^2+20x}$

Vedi la soluzione

La procedura per semplificare una frazione algebrica, cioè una frazione con polinomi, consiste nell’estrarre il fattore comune dal numeratore e dal denominatore della frazione, quindi eliminare i fattori che si ripetono sopra e sotto. sotto la frazione. COSÌ:

$\text{A)} \quad \begin{array}{l} \cfrac{10x^2+30}{5x-20}= \cfrac{5\cdot 2x^2 +5\cdot 6}{5\cdot x-5\cdot 4} = \\[4ex] = \cfrac{5(2x^2+6)}{5(x-4)}= \cfrac{\cancel{5}(2x^2+6)}{\cancel{5}(x-4)} = \\[4ex] = \cfrac{\bm{2x^2+6}}{\bm{x-4}} \end{array}$

$\text{B)} \quad \begin{array}{l} \cfrac{16x^2-8}{24x-32} = \cfrac{8 \cdot 2x^2+8 \cdot (-1)}{8 \cdot 3x-8 \cdot 4} =\\[4ex] = \cfrac{8(2x^2-1)}{8(3x-4)}= \cfrac{\cancel{8}(2x^2-1)}{\cancel{8}(3x-4)} =\\[4ex] = \cfrac{\bm{2x^2-1}}{\bm{3x-4}} \end{array}$

$\text{C)} \quad \begin{array}{l}\cfrac{49x^3+7x}{35x^2-14}=\cfrac{7x\cdot 7x^2+7x\cdot 1}{7 \cdot 5x^2+7\cdot (-2)} =\\[4ex] = \cfrac{7x(7x^2+1)}{7(5x^2-2)}= \cfrac{\cancel{7}x(7x^2+1)}{\cancel{7}(5x^2-2)}=\\[4ex] = \cfrac{\bm{x(7x^2+1)}}{\bm{5x^2-2}} \end{array}$

$\text{D)} \quad \begin{array}{l} \cfrac{8x^4+16x^3-4x^2}{12x^2+20x}=\cfrac{4x^2\cdot 2x^2+4x^2\cdot 4x+4x^2\cdot (-1)}{4x\cdot 3x+4x\cdot 5}=\\[4ex] = \cfrac{4x^2(2x^2+4x-1)}{4x(3x+5)}= \cfrac{\cancel{4}x^{\cancel{2}}(2x^2+4x-1)}{\cancel{4}\cancel{x}(3x+5)}=\\[4ex] = \cfrac{\bm{x(2x^2+4x-1)}}{\bm{3x+5}} \end{array}$

Esercizio 5

Prendi il fattore comune delle seguenti espressioni polinomiali:

$\text{A)} \ \cfrac{7}{3}x^2+ \cfrac{8}{3}x-\cfrac{2}{3}$

$\text{B)} \ \sqrt{12x^3+16}$

$\text{C)} \ x^2+4x-3x-12$

$\text{D)} \ \cfrac{3}{4}x^2+ \cfrac{1}{2}x-\cfrac{5}{6}$

Vedi la soluzione

A) Tutti i termini del polinomio possono essere scomposti fattorialmente al terzo, quindi:

$\begin{array}{l} \cfrac{7}{3}x^2+ \cfrac{8}{3}x-\cfrac{2}{3}= \\[3ex] = \cfrac{1}{3}\cdot 7x^2+ \cfrac{1}{3}\cdot 8x-\cfrac{1}{3}\cdot 2 = \\[3ex] = \mathbf{\cfrac{1}{3}}\bm{\left(7x^2+8x-2\right)} \end{array}$

B) Il divisore comune del polinomio all’interno della radice è 4 ma, poi, possiamo ricavare il divisore comune calcolandone la radice quadrata:

$\begin{array}{l}\sqrt{12x^3+16}= \\[2ex] =\sqrt{4\cdot 3x^3+4\cdot 4}= \\[2ex]=\sqrt{4\left(3x^3+4\right)}= \\[2ex] =\bm{2\sqrt{3x^3+4}}\end{array}$

C) In questo polinomio possiamo applicare il processo di estrazione del fattore comune raggruppando:

$\begin{array}{l}x^2+4x-3x-12= \\[2ex] =x(x+4)-3(x+4) = \\[2ex] = \bm{(x+4)(x-3)}\end{array}$

D) Tutti i coefficienti frazionari del polinomio sono multipli della metà, quindi il fattore comune del polinomio è ½.

$\begin{array}{l}\displaystyle \frac{3}{4}x^2+ \frac{1}{2}x-\frac{5}{6}= \\[4ex] \displaystyle = \frac{1}{2}\cdot\frac{3}{2}x^2+ \frac{1}{2}\cdot x-\frac{1}{2}\cdot\frac{5}{3}= \\[4ex] \displaystyle = \mathbf{\frac{1}{2}}\bm{\left(}\mathbf{\frac{3}{2}}\bm{x^2+x-}\mathbf{\frac{5}{3}} \bm{\right)}\end{array}$

👇👇👇 Cosa ne pensi della spiegazione? Ti è piaciuto? Ricorda inoltre che se hai qualche domanda su come si determina il fattore comune di un polinomio o se non capisci un esercizio, puoi sempre chiedercelo nei commenti, e noi ti risponderemo. 👇👇👇

Estrai o rimuovi il fattore comune

Qual è il fattore comune?

Come ottenere (o estrarre) il fattore comune

Esempi di assunzione (o estrazione) del fattore comune

Esempio 1

Esempio 2

Esempio 3

Esempio 4

Fattore comune per le frazioni

Fattore comune per raggruppamento

Esercizi sui fattori comuni risolti passo dopo passo

Esercizio 1

Esercizio 2

Esercizio 3

Esercizio 4

Esercizio 5

Lascia un commento Annulla risposta