Qui troverai la spiegazione di cosa sia la formula dell’equazione canonica (o segmentale) della retta, detta anche equazione simmetrica. Inoltre, potrai vedere esempi ed esercitarti con esercizi risolti. E, addirittura, troverai come si calcola l’equazione canonica a partire dall’equazione generale (o implicita) della retta.
Qual è l’equazione canonica o segmentale della retta?
Ricorda che la definizione matematica di linea è un insieme di punti consecutivi rappresentati nella stessa direzione senza curve o angoli.
Pertanto, l’ equazione canonica della linea , chiamata anche equazione segmentale della linea , è un modo per esprimere matematicamente qualsiasi linea. Per fare ciò è sufficiente conoscere i punti di intersezione con gli assi coordinati di detta linea.
D’altra parte, in geometria analitica, l’equazione canonica (o segmentale) della retta è anche chiamata equazione simmetrica della retta .
Formula dell’equazione canonica o segmentale della retta
L’equazione canonica o segmentale della retta è l’espressione algebrica della retta che può essere determinata conoscendo i valori in cui la retta interseca l’asse x e l’asse y.
Se una linea interseca gli assi cartesiani nei seguenti punti:
Punto di intersezione con l’asse X:
![]()
Punto di intersezione con l’asse Y:
![]()
La formula per l’equazione canonica (o segmentale) della retta è:
![]()

Va notato che non esiste un’equazione canonica (o segmentale) della retta in nessuno dei seguenti tre casi:
- Quando la linea è verticale, cioè parallela all’asse OY. Perché l’equazione di una linea verticale è

- Quando la linea è orizzontale, cioè parallela all’asse del OX. Perché l’equazione di una linea orizzontale è

- Quando la linea passa per l’origine delle coordinate (punto
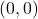
), poiché avremmo allora due indeterminazioni nell’equazione della retta.
Esempio di come trovare l’equazione canonica o segmentale della retta
Per farti comprendere meglio il concetto, risolveremo un problema di equazione segmentale (o canonica) della retta:
- Trova l’equazione canonica o segmentale della retta che passa per i seguenti due punti:
![]()
In questo caso la dichiarazione non ci fornisce 2 punti, bensì i due punti di intersezione con gli assi.
Punto di intersezione della linea con l’asse X:
![]()
Punto di intersezione della linea con l’asse Y:
![]()
Quindi, poiché conosciamo già i due punti di intersezione con gli assi, non ci resta che applicare la formula per l’equazione canonica o segmentale della retta:
![]()
E infine, sostituiamo il valore dei parametri
![]()
E
![]()
nella formula:
![]()
Ora sai qual è l’equazione canonica (o segmentale) della retta. Tuttavia, dovresti sapere che esistono altri modi per esprimere una linea, e tra questi spicca l’ equazione esplicita . Questo tipo di equazione di linea è difficile da comprendere appieno, quindi abbiamo spiegato tutto in dettaglio nella pagina collegata.
Calcolare l’equazione canonica o segmentale della retta a partire dalla sua equazione generale
Abbiamo appena visto un modo per determinare l’equazione canonica o segmentale della retta, ma esistono anche altri metodi:
L’equazione canonica o segmentale di una retta si può ottenere dall’equazione generale (o implicita) di questa stessa retta:
![]()
Per prima cosa cambiamo lato al coefficiente C:
![]()
Successivamente, dividiamo l’intera equazione per il valore del parametro C con segno cambiato:
![]()
![]()
E, attraverso le proprietà delle frazioni, arriviamo alla formula dell’equazione canonica o segmentale della retta:
![]()
Da questa formula consegue quindi che i termini
![]()
E
![]()
dell’equazione canonica di una retta equivalgono alle seguenti espressioni:
![]()
Problemi risolti dell’equazione canonica o segmentale della retta
Esercizio 1
Quali sono i punti di intersezione con gli assi coordinati della retta seguente?
![]()
La retta nell’esercizio è espressa sotto forma di un’equazione canonica o segmentale della retta, la cui formula è:
![]()
Pertanto, i punti in cui la linea interseca gli assi delle coordinate sono:
Punto di intersezione con l’asse X:
![]()
Punto di intersezione con l’asse Y:
![]()
Esercizio 2
Qual è l’equazione canonica o segmentale della retta tracciata?
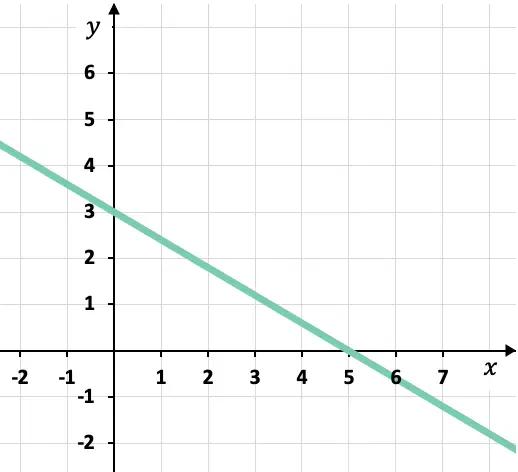
Dal grafico possiamo conoscere i punti in cui la linea incrocia gli assi coordinati:
Punto di intersezione della linea con l’asse X:
![]()
Punto di intersezione della linea con l’asse Y:
![]()
Quindi, una volta conosciuti già i 2 punti di intersezione con gli assi, non ci resta che utilizzare la formula per l’equazione canonica o segmentale della retta:
![]()
E infine, sostituiamo il valore dei parametri
![]()
E
![]()
nella formula:
![]()
Esercizio 3
Calcola l’equazione canonica o segmentale della retta determinata dalla seguente equazione generale (o implicita):
![]()
Per passare da un’equazione generale ad un’equazione segmentale, dobbiamo prima isolare il termine indipendente dell’equazione:
![]()
![]()
In secondo luogo, dividiamo l’intera equazione per il coefficiente sul lato destro dell’equazione:
![]()
![]()
L’espressione sopra è equivalente alla seguente:
![]()
Pertanto l’equazione canonica, segmentale o simmetrica della retta è:
![]()
Esercizio 4
Determinare l’equazione canonica o segmentale di cui è il vettore di direzione
![]()
e passa per il punto
![]()
Per prima cosa troviamo facilmente l’equazione continua della retta dal suo vettore direzione e da un punto che appartiene alla retta:
![]()
![]()
![]()
Ora calcoliamo l’equazione generale della retta moltiplicando trasversalmente le frazioni e raggruppando i termini risultanti:
![]()
![]()
![]()
![]()
È quindi sufficiente convertire l’equazione generale della retta in un’equazione canonica. Per fare ciò, eliminiamo prima il termine indipendente dall’equazione:
![]()
Successivamente, dividiamo l’intera equazione per il coefficiente sul lato destro dell’equazione:
![]()
![]()
L’espressione sopra è equivalente alla seguente:
![]()
Negativo diviso per negativo uguale positivo:
![]()
Le frazioni non possono essere ulteriormente semplificate, quindi l’equazione canonica, segmentale o simmetrica della retta è:
![]()