Moltiplicazione di matrici

In questa pagina vedremo come moltiplicare matrici di dimensioni 2×2, 3×3, 4×4, ecc. Spieghiamo passo dopo passo il procedimento della moltiplicazione di matrici attraverso un esempio, poi troverai esercizi risolti in modo che tu possa anche esercitarti. Infine, imparerai quando due matrici non possono essere moltiplicate e tutte le proprietà di questa operazione con le matrici.

Come moltiplicare due matrici?

Vediamo la procedura per eseguire la moltiplicazione di due matrici con un esempio:

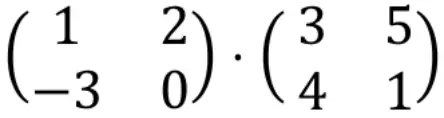
Per calcolare una moltiplicazione di matrici, le righe della matrice di sinistra devono essere moltiplicate per le colonne della matrice di destra.

Quindi per prima cosa dobbiamo moltiplicare la prima riga per la prima colonna. Per fare ciò, moltiplichiamo uno per uno ciascun elemento nella prima riga per ciascun elemento nella prima colonna e aggiungiamo i risultati. Quindi tutto questo sarà il primo elemento della prima riga dell’array risultante. Guarda la procedura:

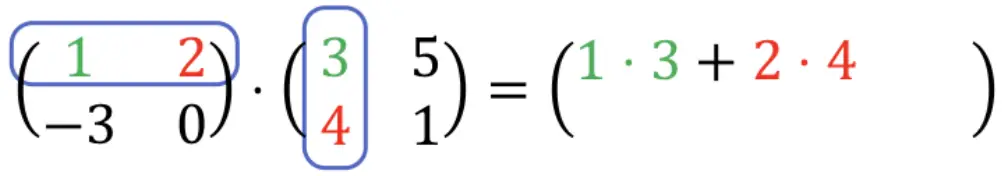
come risolvere la moltiplicazione di matrici 2x2, operazioni con le matrici

1 ⋅ 3 + 2 ⋅ 4 = 3 + 8 = 11. Quindi:

Ora dobbiamo moltiplicare la prima riga per la seconda colonna . Ripetiamo quindi il procedimento: moltiplichiamo uno per uno ogni elemento della prima riga per ogni elemento della seconda colonna, e sommamo i risultati. E tutto questo sarà il secondo elemento della prima riga dell’array risultante:

1 ⋅ 5 + 2 ⋅ 1 = 5 + 2 = 7. Quindi:

Una volta riempita la prima riga della matrice risultante, passiamo alla seconda riga. Moltiplichiamo quindi la seconda riga per la prima colonna ripetendo il procedimento: moltiplichiamo uno per uno ogni elemento della seconda riga per ogni elemento della prima colonna, e sommamo il risultato:

-3 ⋅ 3 + 0 ⋅ 4 = -9 + 0 = -9. Ancora:

Infine, moltiplichiamo la seconda riga per la seconda colonna . Sempre con lo stesso procedimento: moltiplichiamo uno per uno ogni elemento della seconda riga per ogni elemento della seconda colonna, e sommiamo i risultati:

-3 ⋅ 5 + 0 ⋅ 1 = -15 + 0 = -15. Ancora:

E qui finisce la moltiplicazione delle due matrici. Come hai visto, devi moltiplicare le righe per le colonne, ripetendo sempre lo stesso procedimento: moltiplica uno per uno ogni elemento della riga per ogni elemento della colonna, e somma i risultati.

Esercizi di moltiplicazione di matrici risolti

Esercizio 1

Risolvi il seguente prodotto di matrice:

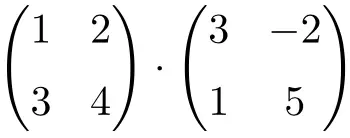
esercizio risolto passo passo prodotto di matrici 2x2, operazioni con matrici

vedi soluzione

È un prodotto di matrici di ordine 2:

$\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix}$

Per risolvere un prodotto di matrici, devi moltiplicare le righe della matrice di sinistra per le colonne della matrice di destra.

Quindi moltiplichiamo prima la prima riga per la prima colonna. Per fare ciò, moltiplichiamo uno per uno ciascun elemento nella prima riga per ciascun elemento nella prima colonna e aggiungiamo i risultati. E tutto questo sarà il primo elemento della prima riga dell’array risultante:

$\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix} = \begin{pmatrix} 1\cdot 3 +2 \cdot 1 & \\[1.1ex] & \end{pmatrix} = \begin{pmatrix} 5 & \\[1.1ex] & \end{pmatrix}$

Ora moltiplichiamo la prima riga per la seconda colonna, per ottenere il secondo elemento della prima riga della matrice risultante:

$\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix} = \begin{pmatrix} -1 & 1\cdot (-2) +2 \cdot 5 \\[1.1ex] & \end{pmatrix} = \begin{pmatrix}5 & 8 \\[1.1ex] & \end{pmatrix}$

Andiamo alla seconda riga, quindi moltiplichiamo la seconda riga per la prima colonna:

$\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix} = \begin{pmatrix} -1 & 8 \\[1.1ex] 3\cdot 3 +4 \cdot 1 & \end{pmatrix}= \begin{pmatrix}5 & 8 \\[1.1ex] 13 & \end{pmatrix}$

Infine, moltiplichiamo la seconda riga per la seconda colonna , per calcolare l’ultimo elemento della tabella:

$\displaystyle \begin{pmatrix} 1 & 2 \\[1.1ex] 3 & 4 \end{pmatrix} \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 1 & 5 \end{pmatrix}= \begin{pmatrix} -1 & 8 \\[1.1ex]1 & 3\cdot (-2) +4 \cdot 5 \end{pmatrix}=\begin{pmatrix} 5 & 8 \\[1.1ex] 13 & 14 \end{pmatrix}$

Quindi il risultato della moltiplicazione di matrici è:

$\displaystyle \begin{pmatrix} \bm{5} & \bm{8} \\[1.1ex]\bm{13} & \bm{14} \end{pmatrix}$

Esercizio 2

Trova il risultato della seguente moltiplicazione di matrici quadrate 2×2:

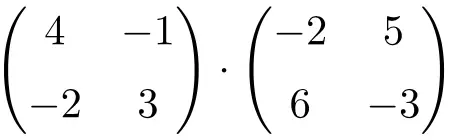
Esercizio risolto passo dopo passo nella moltiplicazione di matrici 2x2, operazioni con le matrici

vedi soluzione

È un prodotto di matrici di dimensione 2×2.

Per risolvere la moltiplicazione, devi moltiplicare le righe della matrice di sinistra per le colonne della matrice di destra:

$\displaystyle \begin{aligned} \begin{pmatrix} 4 & -1 \\[1.1ex] -2 & 3 \end{pmatrix} \cdot \begin{pmatrix} -2 & 5 \\[1.1ex] 6 & -3 \end{pmatrix} & = \begin{pmatrix} 4\cdot (-2)+(-1) \cdot 6 & 4\cdot 5+(-1) \cdot (-3) \\[1.1ex](-2)\cdot (-2)+3 \cdot 6 & (-2)\cdot 5+3 \cdot (-3)\end{pmatrix} \\[2ex] & =\begin{pmatrix} \bm{-14} & \bm{23} \\[1.1ex]\bm{22} & \bm{-19} \end{pmatrix} \end{aligned}$

Esercizio 3

Calcola la seguente moltiplicazione di matrici 3×3:

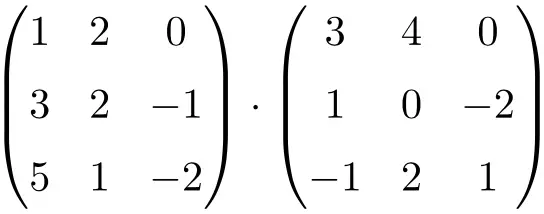
esercizio risolto passo passo moltiplicazione di matrici 3x3, operazioni sulle matrici

vedi soluzione

Per eseguire la moltiplicazione di matrici 3×3, devi moltiplicare le righe della matrice di sinistra per le colonne della matrice di destra:

$\displaystyle \begin{array}{l} \begin{pmatrix} 1 & 2 & 0 \\[1.1ex] 3 & 2 & -1 \\[1.1ex] 5 & 1 & -2 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 & 0 \\[1.1ex] 1 & 0 & -2 \\[1.1ex] -1 & 2 & 1 \end{pmatrix} = \\[7.5ex] =\begin{pmatrix} 1 \cdot 3+2 \cdot 1+ 0 \cdot (-1) & 1 \cdot 4+2 \cdot 0+ 0 \cdot 2 & 1 \cdot 0+2 \cdot (-2)+ 0 \cdot 1 \\[1.1ex] 3 \cdot 3+2 \cdot 1+ (-1) \cdot (-1) & 3 \cdot 4+2 \cdot 0+ (-1) \cdot 2 & 3 \cdot 0+2 \cdot (-2)+ (-1) \cdot 1 \\[1.1ex] 5 \cdot 3+1 \cdot 1+ (-2) \cdot (-1) & 5 \cdot 4+1 \cdot 0+ (-2) \cdot 2 & 5 \cdot 0+1 \cdot (-2)+ (-2) \cdot 1 \end{pmatrix} = \\[7.5ex] =\begin{pmatrix} \bm{5} & \bm{4} & \bm{-4} \\[1.1ex] \bm{12} & \bm{10} & \bm{-5} \\[1.1ex] \bm{18} & \bm{16} & \bm{-4} \end{pmatrix}\end{array}$

Esercizio 4

data la matrice

$A$

$\displaystyle A= \begin{pmatrix} 3 & 1 & -2 \\[1.1ex] 4 & 2 & -1 \end{pmatrix}$

Calcolare:

$\displaystyle 2A\cdot A^t$

vedi soluzione

Per prima cosa calcoleremo la matrice di trasposizione di

$A$

per fare la moltiplicazione. E per creare la matrice di trasposizione, dobbiamo trasformare le righe in colonne. Cioè, la prima riga della matrice diventa la prima colonna della matrice e la seconda riga della matrice diventa la seconda colonna della matrice. Ancora:

$\displaystyle A^t= \begin{pmatrix} 3 & 4 \\[1.1ex] 1 & 2 \\[1.1ex] -2 & -1 \end{pmatrix}$

L’operazione della matrice rimane quindi:

$\displaystyle 2A\cdot A^t = 2 \begin{pmatrix} 3 & 1 & -2 \\[1.1ex] 4 & 2 & -1 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 \\[1.1ex] 1 & 2 \\[1.1ex] -2 & -1 \end{pmatrix}$

Ora possiamo fare i calcoli. Per prima cosa calcoliamo

$2A$

(anche se possiamo anche prima calcolare

$A \cdot A^t$

$\displaystyle \begin{pmatrix} 2 \cdot 3 & 2 \cdot 1 & 2 \cdot (-2) \\[1.1ex] 2 \cdot 4 & 2 \cdot 2 & 2 \cdot (-1) \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 \\[1.1ex] 1 & 2 \\[1.1ex] -2 & -1 \end{pmatrix} =$

$\displaystyle =\begin{pmatrix} 6 & 2 & -4 \\[1.1ex] 8 & 4 & -2 \end{pmatrix} \cdot \begin{pmatrix} 3 & 4 \\[1.1ex] 1 & 2 \\[1.1ex] -2 & -1 \end{pmatrix}$

E, infine, risolviamo il prodotto di matrici:

$\displaystyle \begin{pmatrix} 6 \cdot 3 +2 \cdot 1 + (-4) \cdot (-2) & 6 \cdot 4 +2 \cdot 2 + (-4) \cdot (-1) \\[1.1ex] 8 \cdot 3 +4 \cdot 1 + (-2) \cdot (-2) & 8 \cdot 4 +4 \cdot 2 + (-2) \cdot (-1) \end{pmatrix} =$

$\displaystyle = \begin{pmatrix} \bm{28} & \bm{32} \\[1.1ex]\bm{32} & \bm{42} \end{pmatrix}$

Esercizio 5

Consideriamo le seguenti matrici:

$\displaystyle A=\begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix} \qquad B=\begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix}$

Calcolare:

$\displaystyle A\cdot B - B \cdot A$

vedi soluzione

È un’operazione che combina la sottrazione con le moltiplicazioni di matrici di ordine 2:

$\displaystyle A\cdot B - B \cdot A= \begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix}\cdot \begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix} - \begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix} \cdot \begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix}$

Calcoliamo prima la moltiplicazione a sinistra:

$\displaystyle \begin{pmatrix} 2\cdot (-1) + 4 \cdot 3 & 2\cdot (-2) + 4 \cdot (-3) \\[1.1ex] (-3)\cdot (-1) + 5 \cdot 3 & (-3)\cdot (-2) + 5 \cdot (-3) \end{pmatrix} - \begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix} \cdot \begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix} =$

$\displaystyle= \begin{pmatrix} 10 & -16 \\[1.1ex] 18 & -9 \end{pmatrix} - \begin{pmatrix} -1 & -2 \\[1.1ex] 3 & -3 \end{pmatrix} \cdot \begin{pmatrix} 2 & 4 \\[1.1ex] -3 & 5 \end{pmatrix}$

Ora risolviamo la moltiplicazione a destra:

$\displaystyle \begin{pmatrix} 10 & -16 \\[1.1ex] 18 & -9 \end{pmatrix} - \begin{pmatrix} -1 \cdot 2 +(-2) \cdot (-3) & -1 \cdot 4 +(-2) \cdot 5 \\[1.1ex]3 \cdot 2 +(-3) \cdot (-3) & 3 \cdot 4 +(-3) \cdot 5 \end{pmatrix} =$

$\displaystyle =\begin{pmatrix} 10 & -16 \\[1.1ex] 18 & -9 \end{pmatrix} - \begin{pmatrix} 4 &-14 \\[1.1ex]15 & -3 \end{pmatrix}$

E infine sottraiamo le matrici:

$\displaystyle \begin{pmatrix} 10-4 & -16 -(-14) \\[1.1ex] 18-15 & -9-(-3) \end{pmatrix} =$

$\displaystyle =\begin{pmatrix} \bm{6} & \bm{-2} \\[1.1ex] \bm{3} & \bm{-6} \end{pmatrix}$

Quando non puoi moltiplicare due matrici?

Non tutte le matrici possono essere moltiplicate. Per moltiplicare due matrici, il numero di colonne nella prima matrice deve corrispondere al numero di righe nella seconda matrice.

Ad esempio, la seguente moltiplicazione non può essere eseguita perché la prima matrice ha 3 colonne e la seconda matrice ha 2 righe:

$\displaystyle\begin{pmatrix} 1 & 3 & -2 \\[1.1ex] 4 & 0 & 5 \end{pmatrix} \cdot \begin{pmatrix} 2 & 1 \\[1.1ex] 3 & -1 \end{pmatrix} \ \longleftarrow \ \color{red} \bm{\times}$

Ma se invertiamo l’ordine, si possono moltiplicare. Poiché la prima matrice ha due colonne e la seconda matrice ha due righe:

$\displaystyle \begin{aligned} \begin{pmatrix} 2 & 1 \\[1.1ex] 3 & -1 \end{pmatrix} \cdot \begin{pmatrix} 1 & 3 & -2 \\[1.1ex] 4 & 0 & 5 \end{pmatrix} & = \begin{pmatrix} 2\cdot 1 + 1 \cdot 4 & 2\cdot 3 + 1 \cdot 0 & 2\cdot (-2) + 1 \cdot 5 \\[1.1ex] 3\cdot 1 + (-1) \cdot 4 & 3\cdot 3 + (-1) \cdot 0 & 3\cdot (-2) + (-1) \cdot 5 \end{pmatrix} \\[2ex] & = \begin{pmatrix} \bm{6} & \bm{6} & \bm{1} \\[1.1ex]\bm{-1} & \bm{9} & \bm{-11} \end{pmatrix} \end{aligned}$

Proprietà della moltiplicazione di matrici

Questo tipo di operazione con la matrice ha le seguenti caratteristiche:

La moltiplicazione di matrici è associativa:

$\displaystyle \left( A \cdot B \right) \cdot C = A \cdot \left( B \cdot C \right)$

La moltiplicazione di matrici ha anche la proprietà distributiva:

$\displaystyle A\cdot \left(B+C\right) = A\cdot B + A \cdot C$

Il prodotto di matrici non è commutativo:

$\displaystyle A \cdot B \neq B \cdot A$

Ad esempio, la seguente moltiplicazione di matrici dà un risultato:

$\displaystyle \begin{aligned} \begin{pmatrix} 1 & -1 \\[1.1ex] 2 & 3 \end{pmatrix} \cdot \begin{pmatrix} -2 & 5 \\[1.1ex] 0 & 1 \end{pmatrix} & = \begin{pmatrix} 1\cdot (-2) + (-1) \cdot 0 & 1\cdot 5 + (-1) \cdot 1 \\[1.1ex] 2\cdot (-2) + 3 \cdot 0 & 2\cdot 5 + 3 \cdot 1 \end{pmatrix} \\[2ex] & = \begin{pmatrix} \bm{-2} & \bm{4} \\[1.1ex] \bm{-4} & \bm{13} \end{pmatrix}\end{aligned}$

Ma il risultato del prodotto è diverso se invertiamo l’ordine di moltiplicazione delle matrici:

$\displaystyle \begin{aligned}\begin{pmatrix} -2 & 5 \\[1.1ex] 0 & 1 \end{pmatrix} \cdot \begin{pmatrix} 1 & -1 \\[1.1ex] 2 & 3 \end{pmatrix} & = \begin{pmatrix} -2 \cdot 1 + 5\cdot 2 & -2 \cdot (-1) + 5\cdot 3 \\[1.1ex] 0 \cdot 1 + 1\cdot 2 & 0 \cdot (-1) + 1\cdot 3 \end{pmatrix} \\[2ex] & = \begin{pmatrix} \bm{8} & \bm{17} \\[1.1ex] \bm{2} & \bm{3} \end{pmatrix}\end{aligned}$

Inoltre, qualsiasi matrice moltiplicata per la matrice identità dà come risultato la stessa matrice. Questa è chiamata proprietà di identità moltiplicativa:

$\displaystyle A \cdot I=A$

$\displaystyle I \cdot A=A$

Per esempio:

$\displaystyle \begin{pmatrix} 2 & 7 \\[1.1ex] -6 & 5 \end{pmatrix} \cdot \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix} = \begin{pmatrix} \bm{2} & \bm{7} \\[1.1ex] \bm{-6} & \bm{5} \end{pmatrix}$

Infine, come puoi già intuire, qualsiasi matrice moltiplicata per la matrice zero è uguale alla matrice zero. Questa è chiamata proprietà moltiplicativa dello zero:

$\displaystyle A \cdot 0=0$

$\displaystyle 0\cdot A=0$

Per esempio:

$\displaystyle \begin{pmatrix} 6 & -4 \\[1.1ex] 3 & 8 \end{pmatrix} \cdot \begin{pmatrix} 0 & 0 \\[1.1ex] 0 & 0 \end{pmatrix} = \begin{pmatrix} \bm{0} & \bm{0} \\[1.1ex] \bm{0} & \bm{0}\end{pmatrix}$

Come moltiplicare due matrici?

Esercizi di moltiplicazione di matrici risolti

Esercizio 1

Esercizio 2

Esercizio 3

Esercizio 4

Esercizio 5

Quando non puoi moltiplicare due matrici?

Proprietà della moltiplicazione di matrici

Lascia un commento Annulla risposta